3. Вычислить длину дуги кривой, заданной уравнениями
Билет N 23
1. Найти 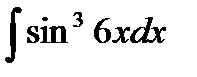
2.Найти ò x Ö 9 - x2 dx
3. Вычислить длину дуги кривой, заданной уравнениями
x = 2 cos3 t,
y = 2 sin3 t ,
0 £ t £ p/4 .
4. Найти производную y”
x = ln t ,
y = arctg t .
5. Найти точки перегиба функции: y = (1 – x2) 3 .
6. Основные правила дифференцирования с примерами.
Билет N 24
1. Найти 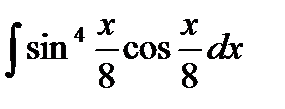
2.Найти ó x dx
õÖ 4 - x2
3. Вычислить длину дуги кривой, заданной уравнениями
r = 5 (1 – cos j ), - p/3 £ j £ 0 .
4. Найти производную
y = log 16 log 5 tg x .
5. Вычислить предел c помощью правила Лопиталя 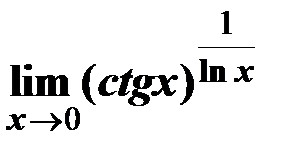 .
.
6. Теоремы Ферма, Ролля, Лагранжа, Коши с примерами и геометрическими иллюстрациями.
Билет N 25
Найти 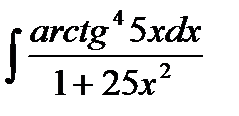
2.Найти ò x Ö 1 - x2 dx
3. Вычислить длину дуги кривой, заданной уравнением:
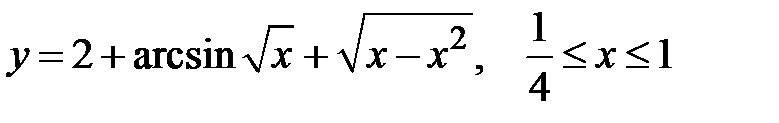
4. Найти дифференциал
y = e4x ( cos 2x + 2 sin 2x ).
5. Найти интервалы выпуклости и вогнутости и точки перегиба кривой:
y = (4x3 – x4) / 5
6. Необходимые условия возрастания-убывания функции с примерами и геометрической иллюстрацией.
Билет N 26
1.Для заданной функции найти дифференциал: 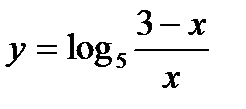
2.Найти 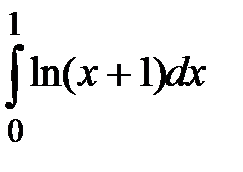
3. Вычислить площадь фигуры, ограниченной линиями:
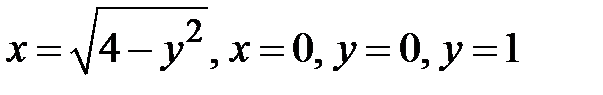
4. Найти 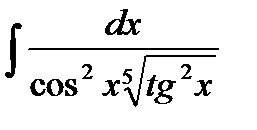
5. Вычислить предел c помощью правила Лопиталя 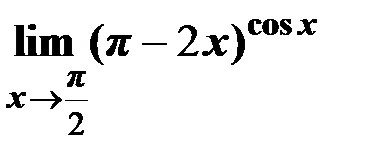 .
.
6. Выпуклость и вогнутость графика функции. Достаточный признак выпуклости-вогнутости. Точка перегиба. Достаточное и необходимое условия существования точки перегиба.
Билет N 27
Для заданной функции найти производную: 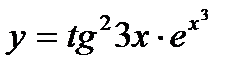
2. Найти ò (5x – 2) e3x dx
3. Вычислить 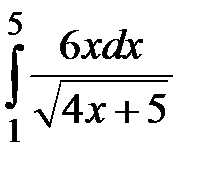 .
.
4. Вычислить площадь фигуры, ограниченной линиями:
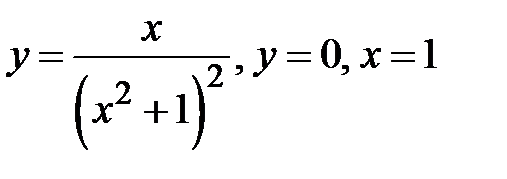
5. Найти наибольшее и наименьшее значения функции на заданном отрезке:
Y = x2 + 16/x – 16, [1;4].
6.Понятия первообразной и неопределенного интеграла. Cвойства и геометрический смысл неопределенного интеграла. Замена переменной в неопределенном интеграле с примером.
Билет N 28
Найти 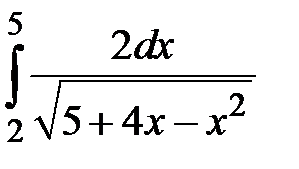
2. Найти 
3. Вычислить площадь фигуры, ограниченной линиями
y = (x – 2) 3 , y = 4x – 8 .
4.Найти производную y’ 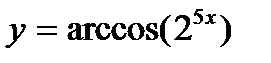
5. Вычислить предел c помощью правила Лопиталя 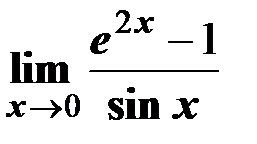 .
.
6. Формула Ньютона-Лейбница с доказательством. Способы вычисления определенного интеграла.
Билет N 29
1. Вычислить 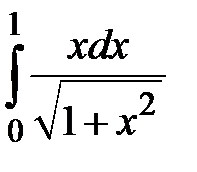
2. Найти 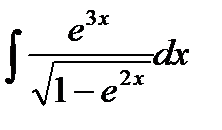
3. Вычислить площадь фигуры, ограниченной линиями:
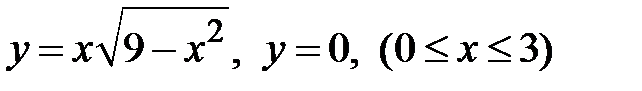
4.Найти производную
y = (arcsin 5x ) tgÖ x .
5. Найти наибольшее и наименьшее значения функции на заданном отрезке:
Y = 4 - x – 4/x2 , [1;4].
6. Критические точки. Достаточный признак существования экстремума. Второй достаточный признак существования экстремума.
Билет N 30
1.Вычислить 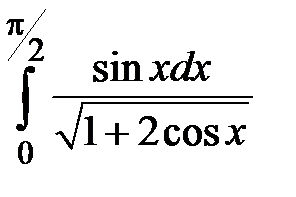
2. Найти 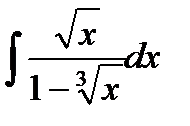
3. Вычислить длину дуги кривой, заданной уравнением:
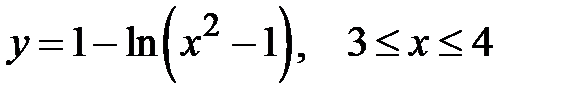
4. Найти производную y”
x = (2t + 3) cos t,
y = 3t3
5. Вычислить предел c помощью правила Лопиталя 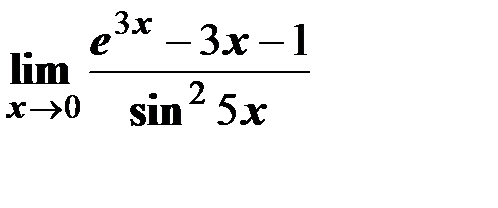 .
.
6. Производная функции, ее геометрический и механический смысл. Связь между понятиями дифференцируемости и непрерывности.








