Расчетная работа по сопротивлению материалов
Задание
Расчетная работа по сопротивлению материалов
Условие задания
Подобрать по условию прочности номер двутавровой балки, изображенной на схеме, при заданной нагрузке (см. в таблице в соответствие с вариантом). Произвести проверку на жёсткость. 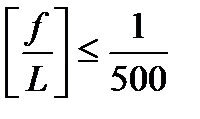 . Запас прочности nm=1,65.
. Запас прочности nm=1,65.
Дано:
| № вар | P1 | P2 | q | M |
L, м | ||||||
| P, кН | α, град | Сеч. | P, кН | α, град | Сеч. | q, кН | α, град | M, кН×м | Сеч. | ||
| 5 | 30 | 90 | III | 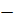 15 15
| 150 | IV | 5 | III 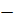 V V
| 10 | III | 2 |
Выполнение задания
Ищем реакции опор RAy , RBy , RBx из уравнений:
Σ X=0 : P2x+ RBx=0;
Σ Y=0 : RAy+P1y 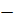 P2y+2qL+RBy=0;
P2y+2qL+RBy=0;
Σ MB=0 : 4RAyL+ M+2qL2 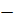 P2yL=0.
P2yL=0.
P1y=P1sin90◦=P1=30 кН
P2y=P2sin150◦=P2×0,5= 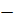 15×0,5=
15×0,5= 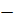 7,5 кН
7,5 кН
P2x=P2cos150=P2( 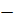 0,866)=15×0,866=12,99 кН
0,866)=15×0,866=12,99 кН
RAy= 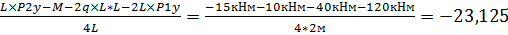 кН
кН
RBy=P2y 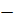 RAy
RAy 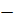 P1y
P1y 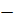 qL=
qL= 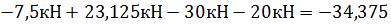 кН
кН
RBx= 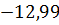 кН
кН
Знак « 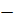 » означает, что нужно поменять направление реакций опор.
» означает, что нужно поменять направление реакций опор.
Построение эпюр
1) Уравнения сил, действующих вдоль оси Х:
I Nx=0;
II Nx=0;
III Nx=0;
IV Nx=P2x=12,99 кН.
2) Распределенная нагрузка:
I qy=0;
II qy=0;
III qy=5кН/м;
IV qy=5кН/м.
3) Перерезающая сила:
I Qy=RAy= 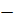 23,125кН;
23,125кН;
II Qy=RAy= 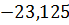 кН;
кН;
III Qy=RAy+P1y+qx= 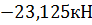 +30кH+5xкH/м; (x=0→Qy=6,875кH; x=L→Qy=16,875кH);
+30кH+5xкH/м; (x=0→Qy=6,875кH; x=L→Qy=16,875кH);
IV Qy=RAy+P1y+q(x+L)  P2y=
P2y= 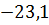 25кH+30кH+5(x+2)кH/м
25кH+30кH+5(x+2)кH/м 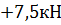 ; (x=0→Qy=24,375кH;x= L→Qy=34,375кH).
; (x=0→Qy=24,375кH;x= L→Qy=34,375кH).
4) Эпюра моментов:
I Mz=RAy×x ; (x=0→Mz=0; x=L→Mz= 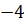 6,25кHм);
6,25кHм);
II Mz=RAy (x+L); (x=0→Mz=  46,25кHм; x=L→Mz=
46,25кHм; x=L→Mz=  92,5кHм);
92,5кHм);
III Mz=RAy (x+2L)+P1×x+ 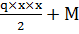 ; (x=0→Mz=
; (x=0→Mz= 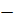 82,5кHм; x=
82,5кHм; x= 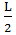 →Mz=
→Mz= 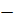 71,125кHм; x=L→Mz=
71,125кHм; x=L→Mz= 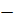 58,75кHм);
58,75кHм);
IV Mz=RAy (х+3L)+M+P1×(x+L) 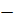 P2y×x+
P2y×x+ 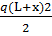 ; (х=0→ Mz=
; (х=0→ Mz= 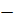 58,75кHм; х=1→ Mz=-31,875кНм; х=L→ Mz=0).
58,75кHм; х=1→ Mz=-31,875кНм; х=L→ Mz=0).
Расчет сечения балки:
Mz= 92,5 кНм; Nx= 12,99 кН;
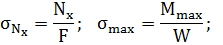
W– момент сопротивления;
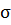 max < [
max < [ 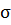 ]; [
]; [ 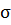 ] =
] = 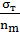
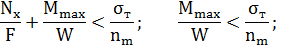
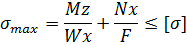
Ст3сп – сталь конструкционная углеродистая обыкновенного качества
Для стали Ст3 σт = 260 МПа, [σ] = σт/nт= 158 МПа
Предварительно рассчитываем сечение без учёта Nx
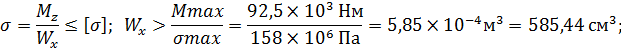
По ГОСТ подходит двутавровая балка №33:
Wx = 597 см3, Ix = 9840 см4, F = 53,8 см2 для Ст3
Проверка:
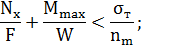
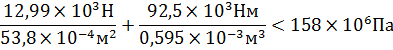
2.4×106Па+155,46×106Па < 158×106 Па
157,86×106Па < 158×106 Па
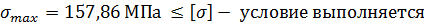
5) Построение эпюры углов поворота сечения балки
I 0<x<L: JEƟx=EJƟ0+ 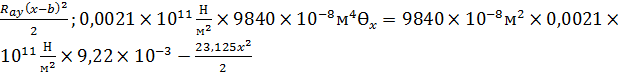
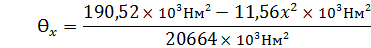
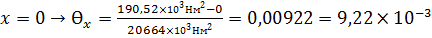 рад
рад
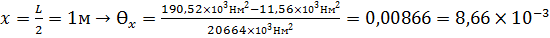 рад
рад
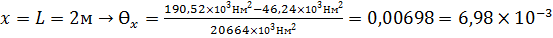 рад
рад
II L<x<2L: тоже самое, что и для I участка 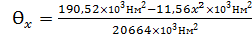
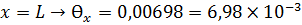 рад
рад
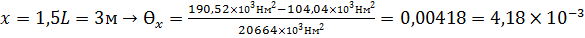 рад
рад
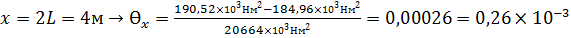 рад
рад
III 2L<x<3L: 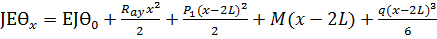
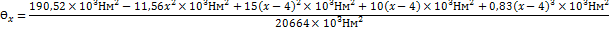
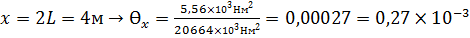 рад
рад
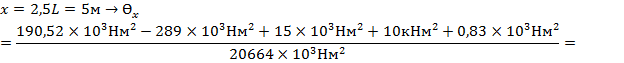
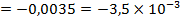 рад
рад
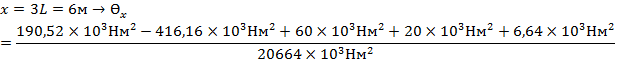
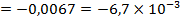 рад
рад
IV 3L<x<4L: 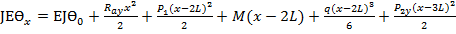
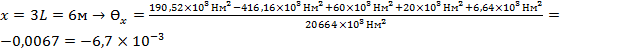 рад
рад
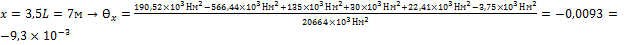 рад
рад
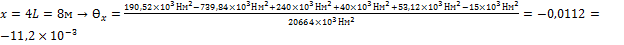 рад
рад
6)Эпюра стрелы прогиба
При x=4L значение прогиба равно 0 ( Vx=0, V0=0)
EJVx=EJV0+EJ 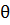 0x+∑
0x+∑ 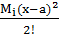 +∑
+∑ 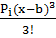 +∑
+∑ 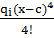
Составляем уравнение для четвертого участка:
0=0+ EJ 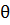 0x+
0x+ 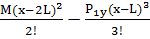 +
+ 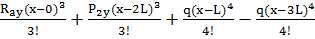
EJ 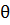 0x=
0x= 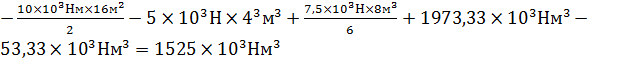
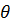 0=
0= 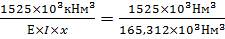 =9,22×
=9,22× 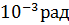
Полное уравнение для 4го участка приравниваем 0 и находим (х), при котором стрела прогиба (f)
EJ 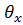 = EJ
= EJ 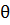 0+∑
0+∑ 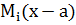 +∑
+∑ 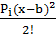 +∑
+∑ 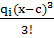
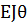 0+
0+ 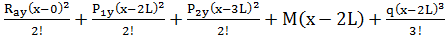 =0
=0
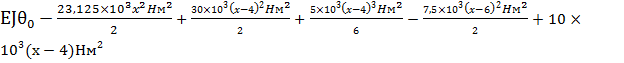 =0
=0
Выберем каждое слагаемое по отдельности
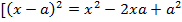 ;
; 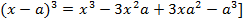
1) 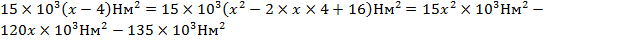
2) 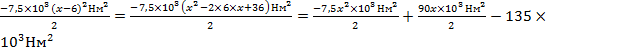
3) 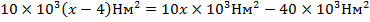
4) 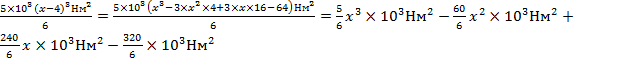
5) 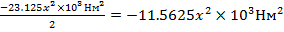
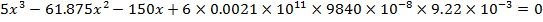
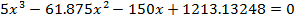
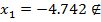
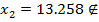
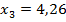
0<x3<8, 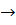 в точке х=4,26 значение
в точке х=4,26 значение  . В этом месте находится стрела прогиба.
. В этом месте находится стрела прогиба.
V0= 0
Vx= 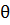 0x+
0x+ 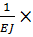 [∑
[∑ 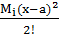 +∑
+∑ 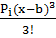 +∑
+∑ 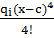 ]
]
Vx= 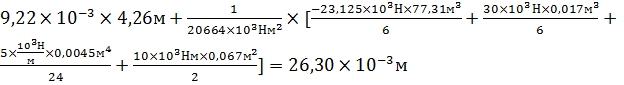
I. 0<x<L : Vx= 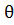 0x +
0x + 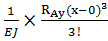
x=0 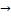 : Vx=0;
: Vx=0;
x=0.5L 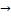 Vx=
Vx= 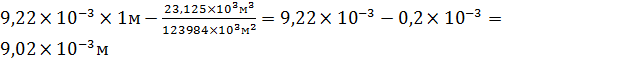 ;
;
x=L 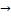 Vx=
Vx= 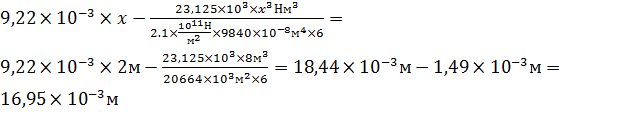 .
.
II. L<x<2L : Vx= 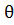 0x +
0x + 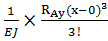
x=L 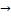 Vx=
Vx= 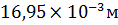 ;
;
x=1,5L 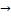 Vx=
Vx= 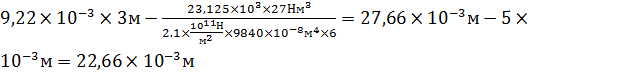 ;
;
x=2L 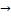 Vx=
Vx= 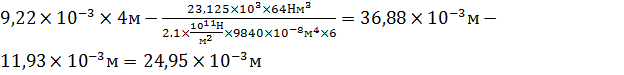 .
.
III. 2L<x<3L : Vx= 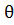 0x +
0x + 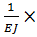 [
[ 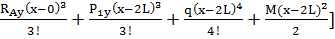
x=2L 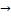 Vx=
Vx= 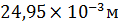 ;
;
x=2,5L 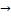 Vx=
Vx= 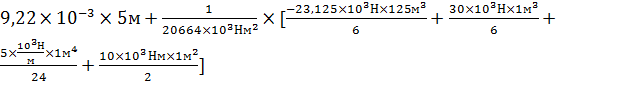
Vx= 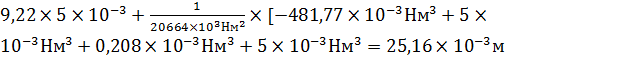 ;
;
x=3L 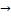 Vx=
Vx= 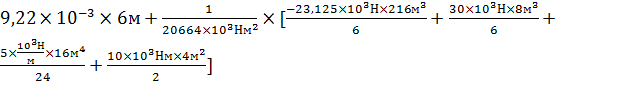
Vx= 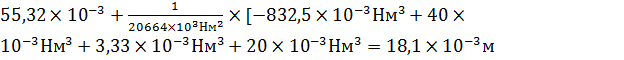 .
.
IV. 3L<x<4L : Vx= 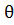 0x +
0x + 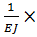 [
[ 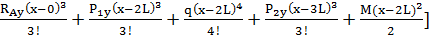
x=3L 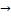 Vx=
Vx= 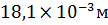 ;
;
x=3,5L 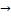 Vx=
Vx= 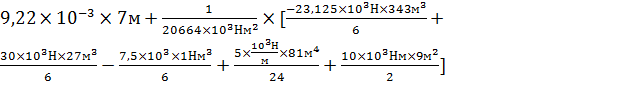
Vx= 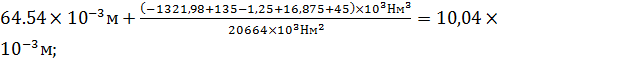
X=4L 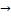 Vx=
Vx= 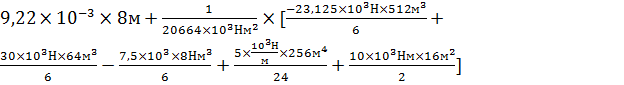
Vx= 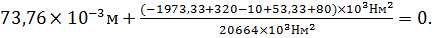
7)Эпюра кривизны
kz = 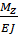
I 0<x<L
x=0  kz = 0
kz = 0 
x=L  kz =
kz = 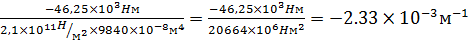
II L<x<2L
x=L 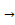 kx =
kx = 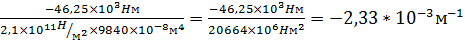
x=2L 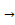 kx =
kx = 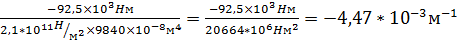
III 2L<x<3L
x=2L 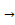 kx =
kx = 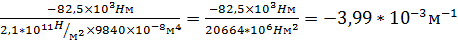
x=2,5L 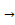 kx=
kx= 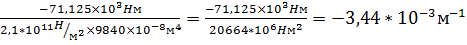
x=3L 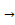 kx =
kx = 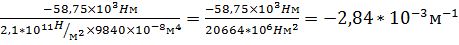
IV 3L<x<4L
x=3L 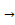 kx =
kx = 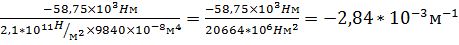
x=3,5L 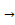 kx =
kx = 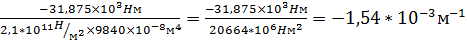
x=4L 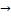 kx =
kx = 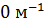
Вывод
Проверили балку на прочность:
по ГОСТу выбрали двутавровую балку №33
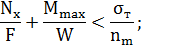
157,86×106Па < 158×106 Па;
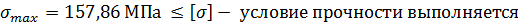 .
.
Проверили балку на жесткость:
на эпюре прогиба определили координату (х) максимального прогиба балки. В точке х=4,26м значение угла поворота сечения  , значит в этом месте находится стрела прогиба
, значит в этом месте находится стрела прогиба  .
.
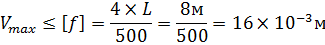
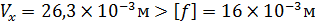 – откуда следует, что условия жесткости балки не выполняются.
– откуда следует, что условия жесткости балки не выполняются.








