Федеральное государственное бюджетное образовательное учреждение
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Тульский государственный университет»
Механико-математический факультет
Кафедра математического моделирования
Комплексный анализ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
К выполнению типового расчета
Направление подготовки: 010800
Механика и математическое моделирование
Квалификация: 62 бакалавр
Форма обучения – очная
Тула – 2012 г.
Комплексный анализ является одной из основных дисциплин для студентов, обучающихся по направлению " Механика, прикладная математика ".
В соответствии с учебным планом данная дисциплина изучается в течение 5-6 семестров. В пятом семестре предусмотрено выполнение типового расчета, в шестом – курсовой работы. Целью данных работ является закрепление общих положений теории в процессе решения конкретных задач. Самостоятельное выполнение этих работ способствует овладению методами комплексного анализа, выработке необходимой интуиции и способности количественно описывать основные механические процессы. В данных методических указаниях приведены примеры заданий к типовому расчету, выполняемому в 5-ом семестре. Необходимые теоретические положения содержатся в курсе лекций по комплексному анализу, а также могут быть почерпнуты из учебников по теории функций комплексного переменного (см. список литературы). Отметим, что наряду с типовыми заданиями могут выполняться и задания, содержащие элементы исследования.
1. Основные задачи ТР
§ изучить основные элементарные функции комплексного переменного;
§ научиться дифференцировать и интегрировать функции комплексного переменного;
§ понимать смысл условий Коши-Римана, уметь восстановить аналитическую функцию по заданной действительной или мнимой части;
§ уметь находить особые точки аналитической функции и определять их тип.
2. Содержание ТР
2.1. Задание на ТР выдается преподавателем.
2.3. ТР оформляется в виде пояснительной записки в соответствии с общепринятыми требованиями. Введение, заключение и список литературы не нужны. Условия задач не приводятся. Текстовые пояснения должны быть сведены к минимуму, а вот все математические выкладки необходимо привести полностью: пропуски в решении недопустимы! Каждая задача оформляется следующим образом: в начале – номер задачи, далее – решение, и в конце – ответ, обведенный в рамку (или подчеркнутый). В ряде задач необходимо, помимо текстового ответа, привести графический (см. раздел 3).
3. Пояснения к задачам, составляющим ТР
Пояснения даются на типичных примерах.
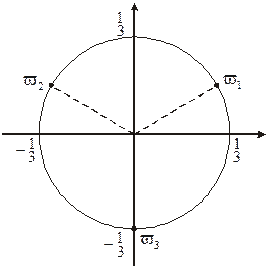
3.1. Найти все значения корня
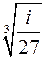
Используется формула
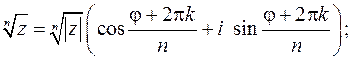
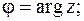
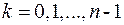
В данном случае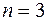 
. Найдем модуль и аргумент 
:
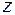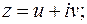
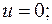
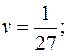
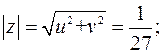
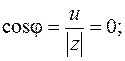
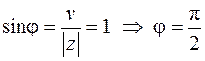
Получим
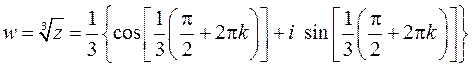
1) 
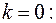
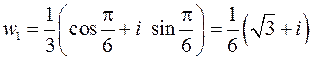
2) 
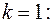
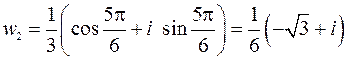
3) 
 |
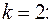
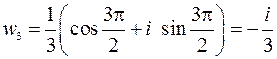
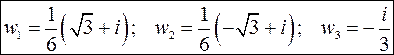
3.2. Представить в алгебраической форме
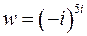
Прологарифмируем
,
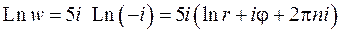где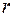 
– модуль числа 
, 
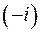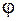– его аргумент, 
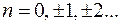Найдем 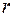и :
.
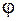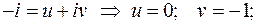
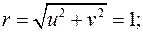
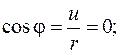
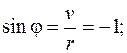
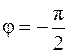Получим
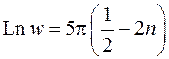
Отсюда
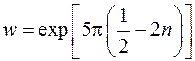– действительное число.
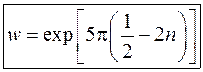
3.3. Представить в алгебраической форме
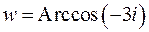
Так как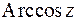 
– функция, обратная косинусу, можно записать
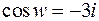
Далее используем формулу
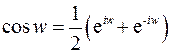
и, вводя обозначение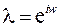 
, получим
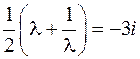
– уравнение относительно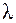 
, которое легко приводится к квадратному
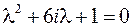
Его решение имеет вид
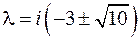
Получим
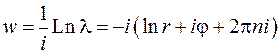
где 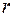и 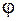– модуль и аргумент числа .
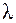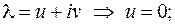
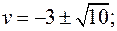
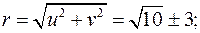
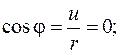
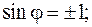
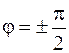
Получим окончательно
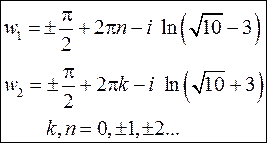
3.4. Вычертить область, заданную неравенствами
, 
, 
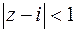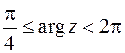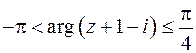
Рассмотрим первое неравенство
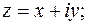
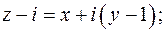
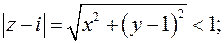
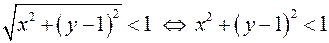
– внутренние точки круга единичного радиуса с центром в точке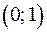 
.
Второе неравенство. Введем полярные координаты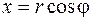 
; 
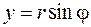. Получим 
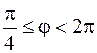– часть плоскости, ограниченную лучам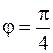и 
и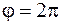 
.
Третье неравенство. Запишем
 |
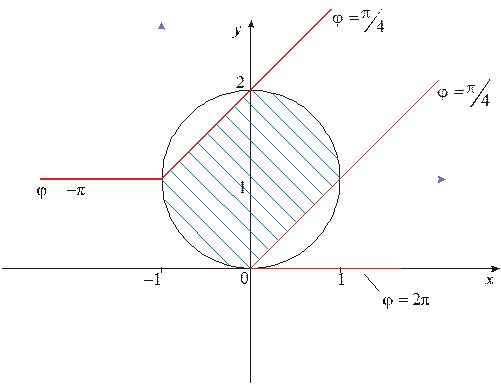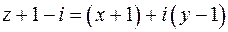. Перенесем начало координат в точку с координатами 
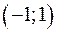, введем в новой системе координат полярные координаты и получим 
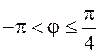– часть плоскости, ограниченную лучам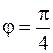и и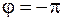 
.
Искомая область заштрихована.
3.5. Определить вид кривой
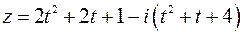
Разделяя действительные и мнимые части, получим параметрические уравнения кривой
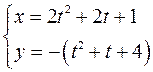
Исключим параметр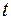 
. Из второго уравнения 
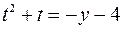. Подставим в первое 
.
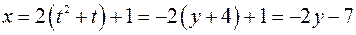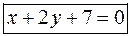- прямая.
3.6. Восстановить аналитическую функцию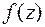 
по известной мнимой части 
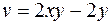и значению 
.
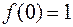Исходными уравнениями служат условия Коши-Римана:
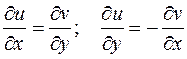
Получим
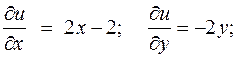
Интегрируем второе уравнение:
,
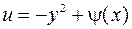где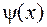 
- некоторая функция 
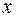. Она определяется из первого уравнения:
,
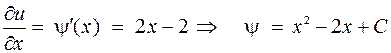где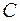 
- постоянная интегрирования. Получим:
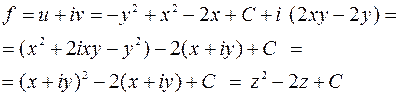
Из условия 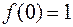следует, что 
.
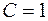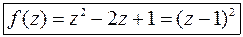
3.7. Вычислить контурный интеграл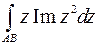 
; 
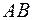- отрезок прямой 
, 
.
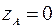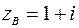Уравнение прямой, проходящей через точки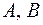 
, имеет, очевидно, вид 
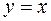. Поэтому на этой прямой 
.
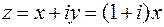Найдем:
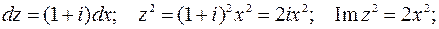
Получим:
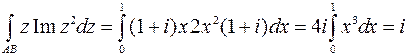
3.8. Найти разложение данной функции по степеням 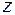в окрестности точки 
:
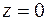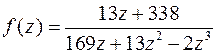
Используем известное разложение:
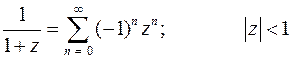
Разложим функцию на элементарные дроби. Найдем корни знаменателя
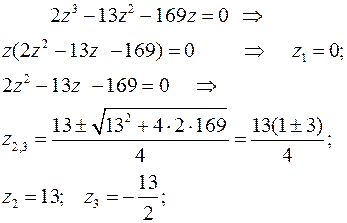
Получим:
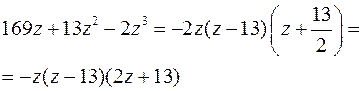
Далее:
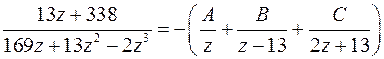
Отсюда следует:
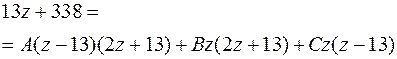
Полагая последовательно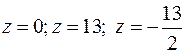 
, определяем константы 
: 
.
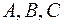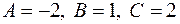Приходим к выражению:
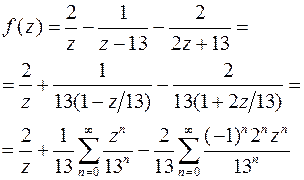
Ряд сходится при:
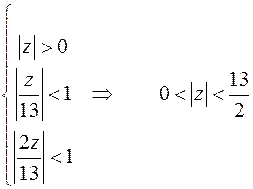
Окончательно получаем:
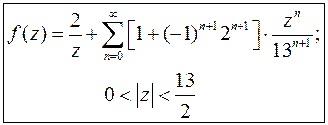
3.9. Найти разложение данной функции по степеням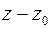 
в окрестности точки 
:
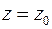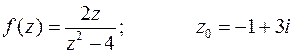
Используем то же разложение, что и в п.3.8. Разложим 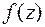на элементарные дроби:
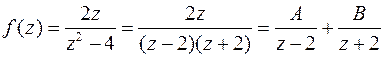
откуда следует:
.
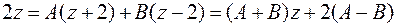Получим:
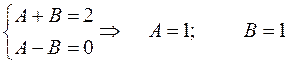
Приходим к выражению:
.
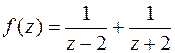Ведем в рассмотрение новую переменную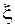 
: 
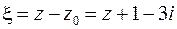
Тогда
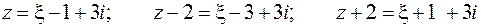
Получим:
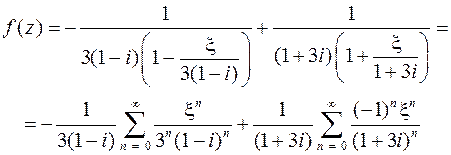
Сходимость обеспечена при выполнении условий:
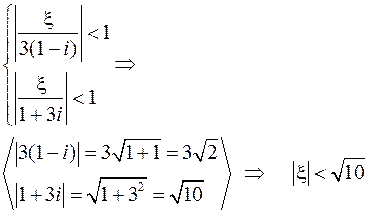
Окончательно:
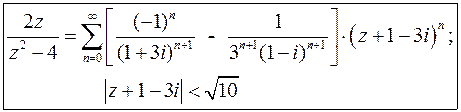
3.10. Данную функцию разложить в ряд Лорана в окрестности точки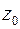 
:
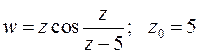
Введем новую переменную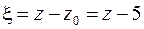 
. Получим:
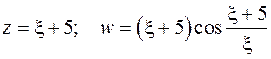
Преобразуем косинус:
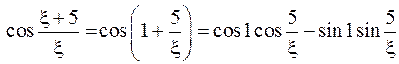
Используем известные разложения для косинуса и синуса:
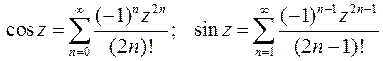
Получим:
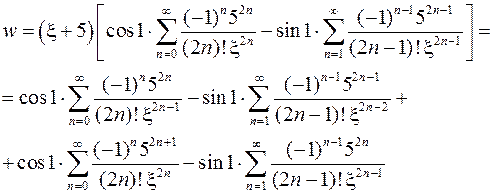
Приведем подобные члены:
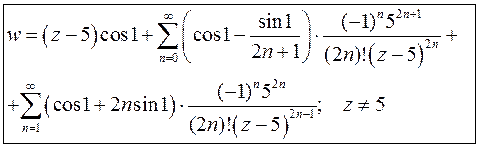
3.11. Определить тип особой точки 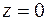для данной функции:
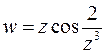
Ищем предел функции:
,
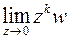где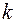 
- некоторое целое число. Если существует 
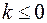, такое, что предел конечен и отличен от нуля, то 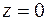- устранимая особая точка; если существует такое конечное 
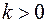, что предел конечен и отличен от нуля, то 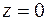- полюс 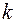-го порядка; если невозможно найти конечное 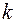, чтобы предел был конечен и отличен от нуля, то 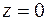- существенно особая точка.
Используем разложение для косинуса (см. 3.10)
Получим:
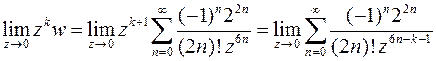
Каким бы большим ни было число 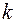, всегда найдется 
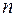, такое, что 
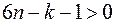. Значит, 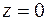- существенно особая точка.
3.12. Для данной функции найти изолированные особые точки и определить их тип:
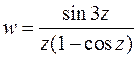
Функция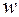 
определена при всех конечных 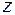за исключением тех, которые обращают в нуль знаменатель. Это 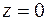и корни уравнения 
.
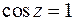Решим это уравнение, используя формулу:
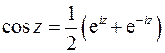
Обозначим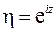 
и получим:
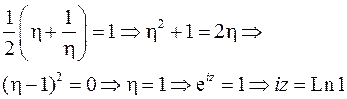
откуда следует:
,
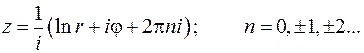где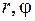 
- модуль и аргумент 
.
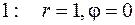Получим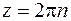 
- уравнение имеет только действительные корни.
Определим тип особых точек:
1)
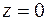
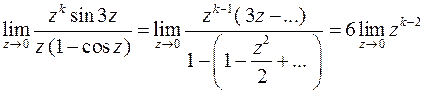
Конечный предел, отличный от нуля, получается при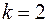 
. Таким образом, точка 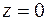- полюс второго порядка.
Основные элементарные функции, входящие в числитель и знаменатель, раскладываются в ряды по степеням 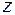(эти разложения известны); бесконечно-малые величины высших порядков малости отбрасываются.
2) 
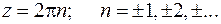
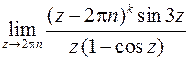
Здесь, как и выше, ищется такое целое 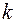, чтобы предел был конечен и отличен от нуля.
Следует выполнить замену переменной: новая переменная должна стремиться к нулю.
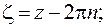
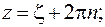
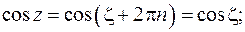
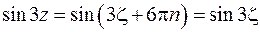
Получим
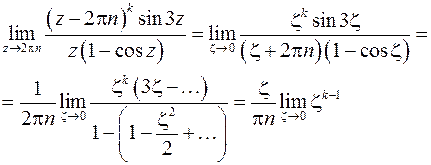
Отличный от нуля конечный предел получается при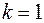 
: точки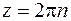 
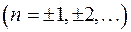– полюсы первого порядка.
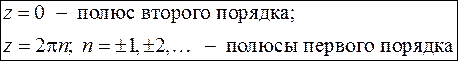
Основная литература
1. Лавит И.М. Конспект лекций дисциплины «Комплексный анализ». 2012. (ресурс кафедры).
Дополнительная литература
1. Привалов И.И. Введение в теорию функций комплексного переменного: учебник / И.И. Привалов .— 15-е изд., стер .— СПб. ; М. ; Краснодар : Лань, 2009 .— 432 с. (1 экз.)
2. Рудкевич, Е.А. Методические указания к решению задач по теме "Функции комплексного переменного" / Е.А.Рудкевич; ТулГУ .— Тула, 2003 .— 49 с. (1 экз.)
3. Рудкевич, Е.А. Функции комплексного переменного и операционное исчисление (методы решения задач : учебное пособие / Е.А.Рудкевич;ТулГУ .— Тула, 2004 .— 64 с. (1 экз.)
4. Лунц Г.Л. Функции комплексного переменного с элементами операционного исчисления: учебник для вузов / Г.Л.Лунц, Л.Э.Эльсгольц. — 3-е изд. — СПб.: Лань, 2006. — 304 с. (5 экз.)
5. Лаврентьев М.А. Методы теории функций комплексного переменного / М.А.Лаврентьев, Б.В.Шабат. — 7-е изд., стер. — М.: Лань, 2007. — 688 с. (10 экз.)
Рассмотрено на заседании кафедры
Протокол №_____ от "___" ______________ 2012 г.
Зав. кафедрой ____________________ А.А. Маркин