Федеральное государственное бюджетное образовательное учреждение
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Тульский государственный университет»
Механико-математический факультет
Кафедра математического моделирования
Комплексный анализ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
К выполнению курсовой работы
Направление подготовки: 010800
Механика и математическое моделирование
Квалификация: 62 бакалавр
Форма обучения – очная
Тула – 2012 г.
Комплексный анализ является одной из основных дисциплин для студентов, обучающихся по направлению " Механика, прикладная математика ".
В соответствии с учебным планом данная дисциплина изучается в течение 5-6 семестров. В пятом семестре предусмотрено выполнение типового расчета, в шестом – курсовой работы. Целью данных работ является закрепление общих положений теории в процессе решения конкретных задач. Самостоятельное выполнение этих работ способствует овладению методами комплексного анализа, выработке необходимой интуиции и способности количественно описывать основные механические процессы. В данных методических указаниях приведены примеры заданий к курсовой работе, выполняемой в 6-ом семестре. Необходимые теоретические положения содержатся в курсе лекций по комплексному анализу, а также могут быть почерпнуты из учебников по теории функций комплексного переменного (см. список литературы). Отметим, что наряду с типовыми заданиями могут выполняться и задания, содержащие элементы исследования.
1. Основные задачи КР
§ использовать теорему о вычетах для нахождения интегралов;
§ уметь находить изображения по заданному оригиналу и оригинал по заданному изображению (для преобразования Лапласа);
§ уметь решать обыкновенные линейные дифференциальные уравнения с постоянными коэффициентами и их системы операционным методом;
§ находить образ заданной области при конформном отображении;
§ использовать конформные отображения для решения краевых задач.
2. Содержание КР
2.1. Задание на КР выдается преподавателем.
2.3. КР оформляется в виде пояснительной записки в соответствии с общепринятыми требованиями. Введение, заключение и список литературы обязательны. Условия задач приводятся. Текстовые пояснения должны быть сведены к минимуму, а вот все математические выкладки необходимо привести полностью: пропуски в решении недопустимы! Каждая задача оформляется следующим образом: в начале – номер задачи, далее – решение, и в конце – ответ, обведенный в рамку (или подчеркнутый). В ряде задач необходимо, помимо текстового ответа, привести графический (см. раздел 3).
3. Пояснения к задачам, составляющим КР
Пояснения даются на типичных примерах.
3.1. Вычислить интеграл
 |
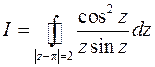
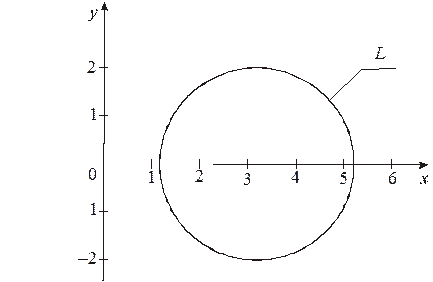Контур интегрирования представляет собой окружность радиусом 2 с центром в точке 
Для вычисления интеграла используем теорему о вычетах. Найдем особые точки подынтегральной функции – в данном случае это точки, в которых знаменатель обращается в нуль. Это, во-первых, точка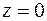 
, и корни уравнения
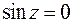
Для решения этого уравнения используем формулу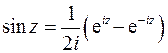 
. Введем обозначение 
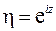и получим
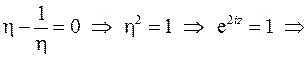
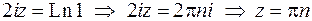
В область, ограниченную контуром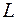 
, попадает только одна особая точка: 
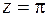. Определим ее тип:
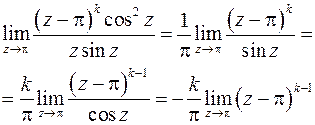
Отличный от нуля конечный предел будет при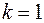 
: точка 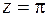– полюс первого порядка. Найдем вычет в этой точке
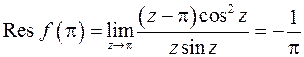
Искомый интеграл равен
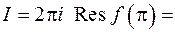
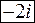
3.2. Вычислить интеграл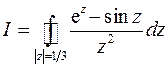 
Контур интегрирования – окружность радиусом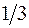 
с центом в начале координат. Используем теорему о вычетах. Подынтегральная функция имеет только одну особую точку – 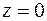, и эта точка находится внутри контура интегрирования. Найдем вычет в этой точке. Вначале определим тип особой точки.
Найдем
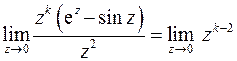
Конечный и отличный от нуля предел достигается при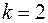 
: точка 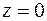– полюс второго порядка. В соответствии с теоремой о вычетах
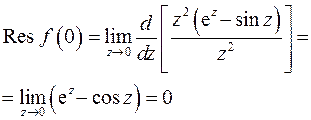
Таким образом,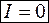 
3.3. Вычислить интеграл
 |
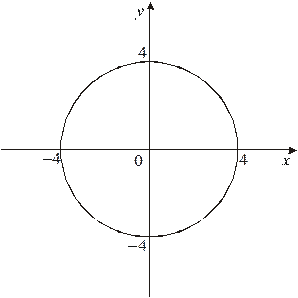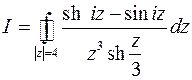
Контур интегрирования – окружность радиусом 4 с центом в начале координат. Подынтегральная функция имеет особую точку 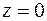и точки, являющиеся корнями уравнения
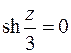
Решение этого уравнения получается с использованием формулы
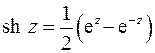
Обозначим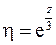 
и получим
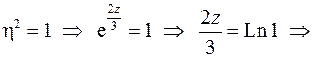
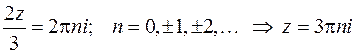
Внутрь контура интегрирования попадает только один корень: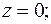 
.
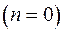Определим тип особой точки :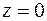
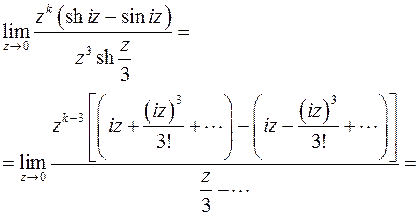
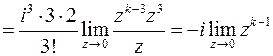
Конечный и отличный от нуля предел получится при 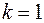: точка 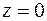– полюс первого порядка. Вычет равен
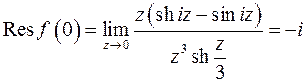
По теореме о вычетах
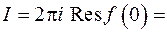
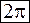
3.4. Вычислить интеграл
 |
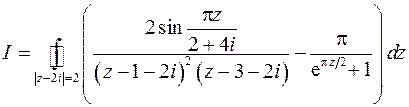
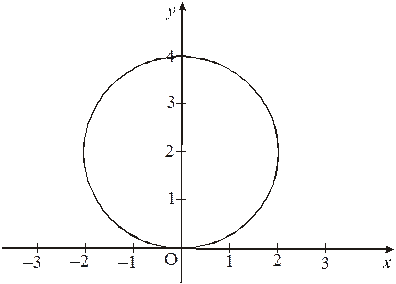Контур интегрирования – окружность радиуса 2 с центром в точке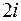 
.
Подынтегральная функция представляет собой сумму двух слагаемых. Удобно представить интеграл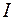 
как сумму двух интегралов 
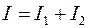, вычисляемых независимо друг от друга.
1) 
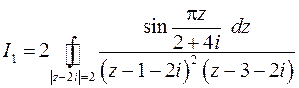
В данном случае удобно перейти к новой переменной (что то же – перенести начало координат в центр окружности):
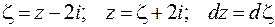
Получим
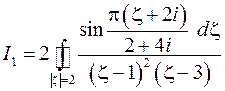
Находим интеграл с помощью теоремы о вычетах. Особые точки подынтегральной функции – нули знаменателя – равны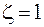 
и 
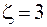. Внутрь контура интегрирования попадает лишь одна точка 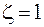. Определим ее тип
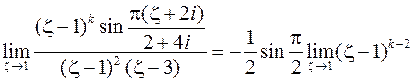
Конечный и отличный от нуля предел получается при 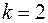: точка 
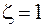- полюс второго порядка. Найдем вычет в точке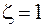
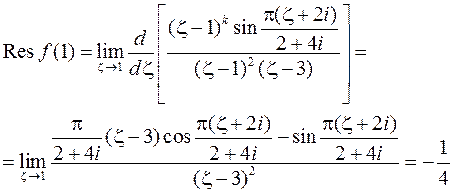
Тогда
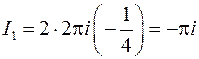
2) 
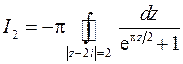
Применяем теорему о вычетах. Находим особые точки подынтегральной функции – корни уравнения:
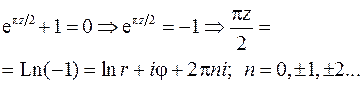
Здесь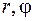 
модуль и аргумент числа 
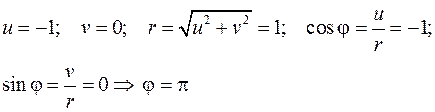
Получим:
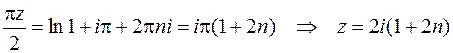
В область, ограниченную контуром интегрирования, попадает только одна особая точка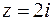 
. Определим ее тип. Удобно, как и в предыдущем случае, перейти к новой переменной 
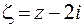. Тогда:
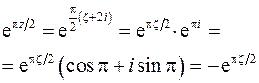
(использована формула Эйлера).
Получим: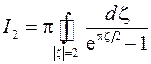 
;
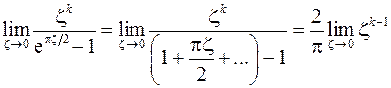
Конечный и отличный от нуля предел будет при 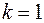, следовательно, точка 
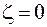- полюс первого порядка. Найдем вычет:
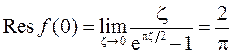
Получим:
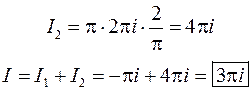
3.5. Вычислить интеграл
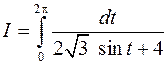
Этот интеграл преобразуется к интегралу от аналитической функции по окружности единичного радиуса. Воспользуемся экспоненциальной формой комплексного числа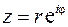 
и отождествим 
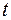с аргументом комплексного числа 
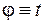. Тогда на окружности единичного радиуса
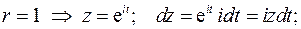
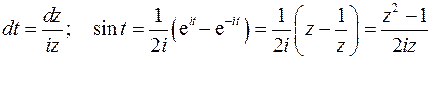
Получим
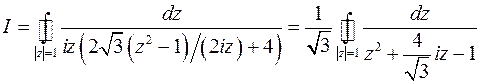
Находим интеграл с использованием теоремы о вычетах. Ищем особые точки подынтегральной функции – корни уравнения
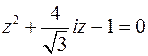
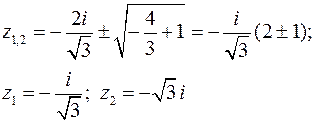
Внутри контура интегрирования оказывается только один корень -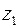 
. Определим тип особой точки :
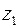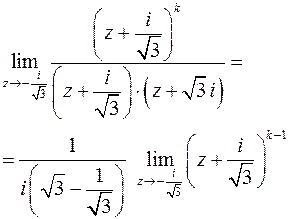
Конечный и отличный от нуля предел будет при 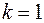. Следовательно, точка 
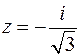- полюс первого порядка. Найдем:
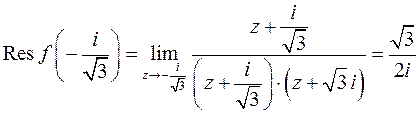
Получим:
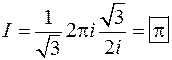
3.6. Вычислить интеграл
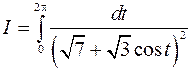
Решаем задачу так же, как задачу 3.17: преобразуем интеграл 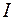в интеграл от аналитической функции по единичной окружности. Используем формулу
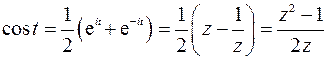
Получим
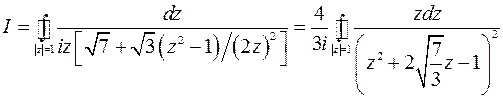
Находим интеграл с помощью теоремы о вычетах. Ищем особые точки подынтегральной функции – корни уравнения
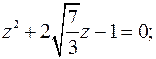
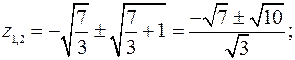
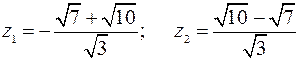
Очевидно, что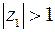 
. Покажем, что 
.
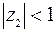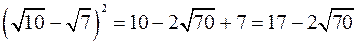
Предположим, что выполняется неравенство
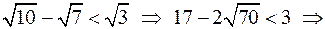
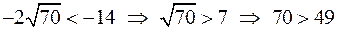
Неравенство доказано.
Таким образом, внутри единичной окружности находится только точка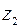 
. Определим тип особой точки :
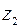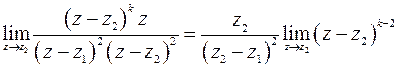
Конечный и отличный от нуля предел получается при 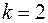– точка 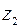является полюсом второго порядка. Найдем вычет в этой точке
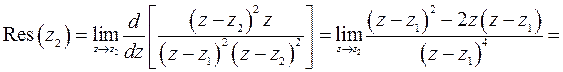
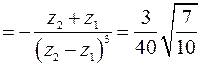
Получим
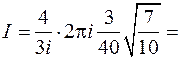
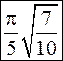
3.7. Вычислить интеграл
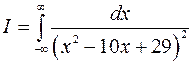
Убедимся в непрерывности подынтегральной функции. Разрывы могут быть только в точках, где знаменатель обращается в нуль. Найдем эти точки:
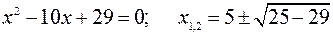– дискриминант отрицательный. Следовательно, подынтегральная функция непрерывна.
Преобразуем интеграл 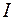к интегралу от функции комплексного переменного.
 |
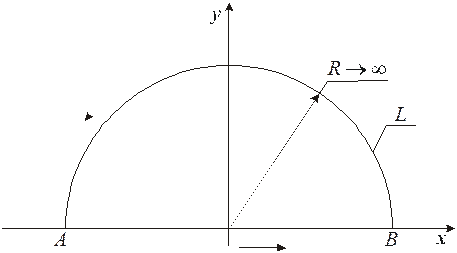Рассмотрим интеграл вдоль контура :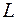
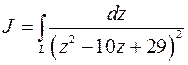
Интеграл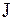 
равен сумме интегралов вдоль участка 
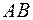(действительная ось) и участка 
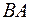(полуокружность). Пусть 
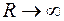. Тогда, очевидно,
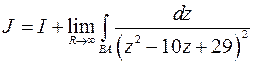
Найдем второе слагаемое. На контуре 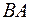получается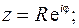 
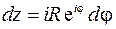. Получаем
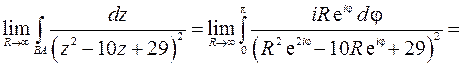
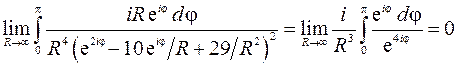
Таким образом,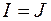 
. Для вычисления интеграла 
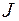применяем теорему о вычетах. Контур 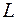при 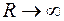охватывает всю верхнюю полуплоскость. Значит, необходимо найти вычеты в особых точках, у которых мнимая часть положительна. Ищем особые точки:
.
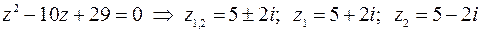Сформулированному условию удовлетворяет только корень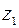 
. Определим тип особой точки
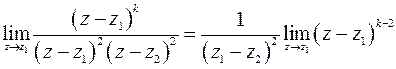
Конечный и отличный от нуля предел получается при 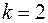. Значит, точка 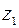является полюсом второго порядка. Найдем вычет
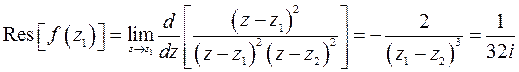
Получим интеграл
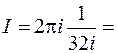
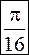
3.8. Вычислить интеграл
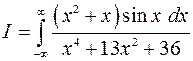
Представим интеграл в виде суммы
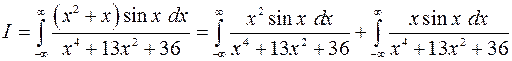
Так как подынтегральная функция первого слагаемого – нечетная, первое слагаемое равно нулю. Получаем
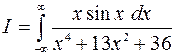
С использованием формулы Эйлера
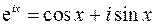
данный интеграл можно представить следующим образом
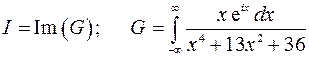
Для вычисления интеграла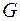 
рассмотрим интеграл от функции комплексного переменного
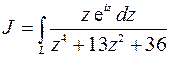
где контур интегрирования – тот же, что и в предыдущей задаче. Запишем (при )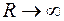
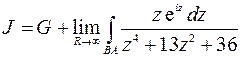
Рассмотрим поведение множителя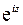 
при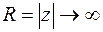 
:
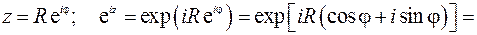
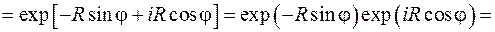
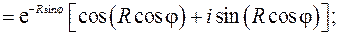
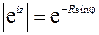
При выводе использовалась формула Эйлера. Пр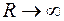и и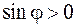 
(а именно этот случай реализуется при движении вдоль контура 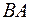) модуль 
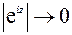. Следовательно, подынтегральная функция также будет стремиться к нулю:
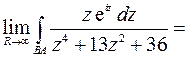
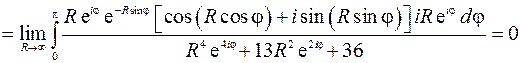
Получаем 
. Последний интеграл находим с помощью теоремы о вычетах. Ищем особые точки подынтегральной функции, лежащие в верхней полуплоскости
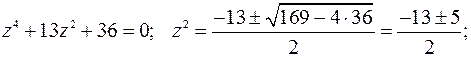
Получим
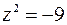и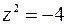 
Особые точки, лежащие в верхней плоскости:
Подынтегральную функцию можно представить в виде
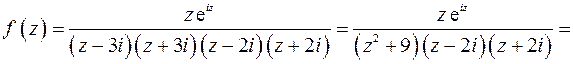
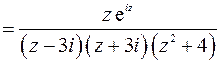
Обе особые точки – полюсы первого порядка. Найдем вычеты в особых точках
1) 
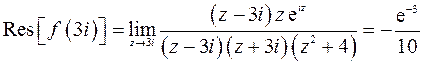
2) 
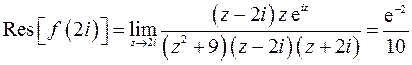
Получим
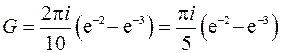
Отделяем мнимую часть
 |
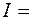
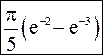
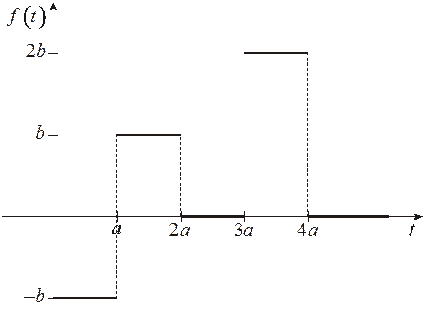3.9. По данному графику оригинала найти изображение
Изображение находится по формуле
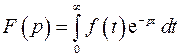
В данном случае
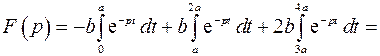
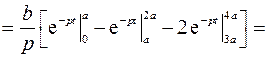
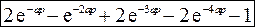
3.10. Найти оригинал по заданному изображению
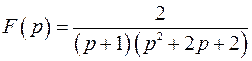
Оригинал находится как сумма вычетов аналитической функции
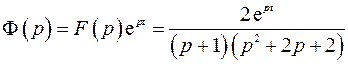
по всем особым точкам. Найдем особые точки – корни знаменателя
.
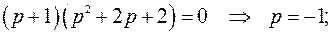
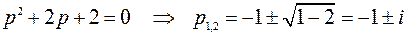Получим особые точки:
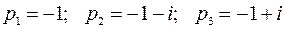
Функцию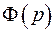 
можно записать в виде
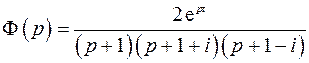
Очевидно, что все особые точки – полюсы первого порядка. Найдем вычеты в особых точках:
1) 
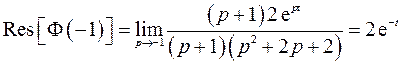
2) 
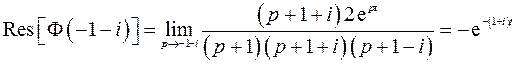
3) 
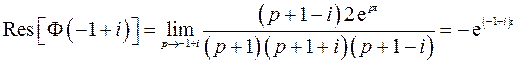
Получим оригинал
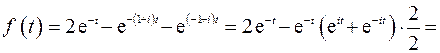
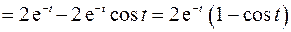
Была использована формула
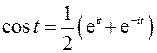
Таким образом, получим
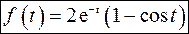
3.11. Найти решение дифференциального уравнения, удовлетворяющее условиям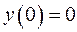 
, 
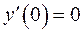
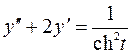
Решение уравнения получаем с использованием операционного метода и формул Дюамеля. Решим вспомогательное уравнение
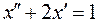
при нулевых начальных условиях: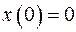 
, 
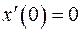. Умножим обе части уравнения на 
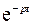и проинтегрируем по 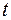в пределах от 0 до 
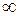, то есть, применим к уравнению преобразование Лапласа. Пусть 
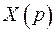– изображение функции 
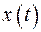; тогда 
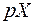будет изображением ее производной 
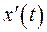. Найдем изображение единичной функции
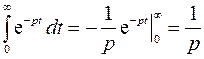
Получим
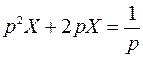
или
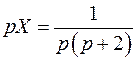
Производная 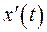найдется как сумма вычетов функции
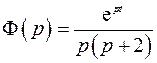
Особые точк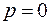и 
и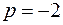 
, очевидно, полюсы первого порядка. Найдем вычеты в этих точках
1) 
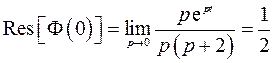
2) 
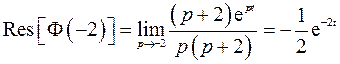
Получим
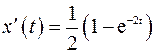
Для нахождения функции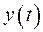 
используем формулу Дюамеля
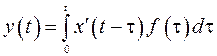
где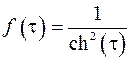 
– функция, стоящая в правой части исходного уравнения. Получим
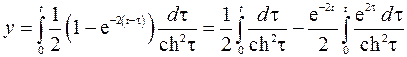
Первый интеграл – табличный
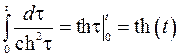
При вычислении второго интеграла используем формулу
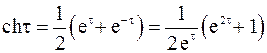
Получим:
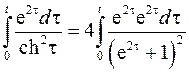
Введем новую переменную:
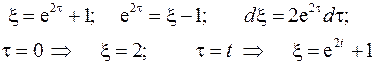
Тогда
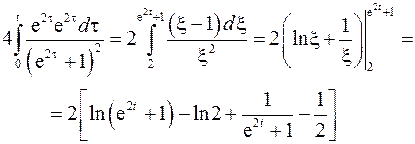
Получим:
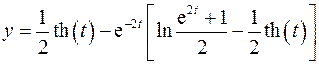
Окончательно:
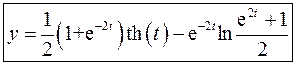
3.12. Операционным методом решить задачу Коши
Это уравнение решается аналогично предыдущему. Предварительно нужно выполнить замену переменной таким образом, чтобы новая зависимая переменная удовлетворяла нулевым начальным условиям. Итак, ищем решение в виде:
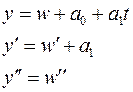
Определяем постоянные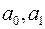 
из условия:
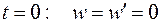
Получим:
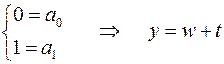
Подставим в уравнение:
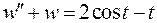
Решим вспомогательное уравнение:
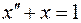
при однородных (нулевых) начальных условиях. Применяя операционный метод, получим:
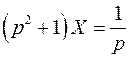
Откуда следует, что
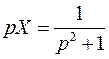
Производная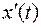 
находится как сумма вычетов функции
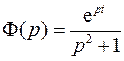
по всем особым точкам. Особые точки – корни уравнения:
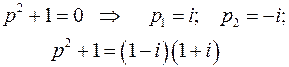
- полюсы первого порядка. Ищем вычеты:
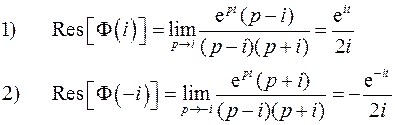
Получим:
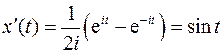
По формуле Дюамеля
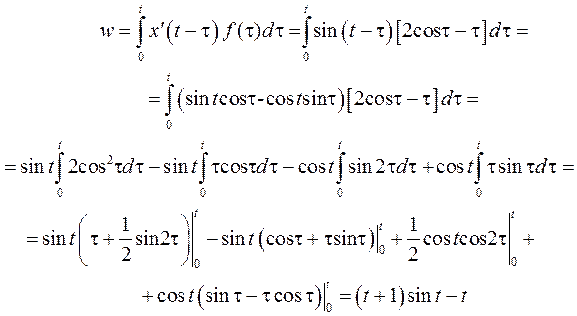
При вычислении интегралов использована формула интегрирования по частям. Получаем ответ
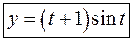
3.13. На материальную точку массы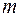 
действует сила сопротивления 
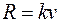, пропорциональная скорости 
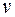. Какое расстояние пройдет точка за неограниченное время, если ей сообщена начальная скорость 
?
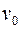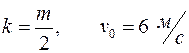
Составим расчетную схему
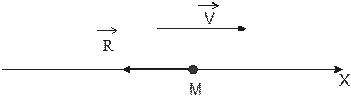
Уравнение движения:
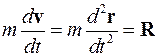
или
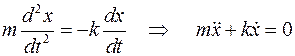
Начальные условия:
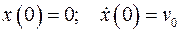
Точка над символом обозначает дифференцирование по времени. Решаем задачу операционным методом:
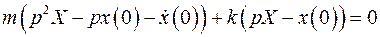
или
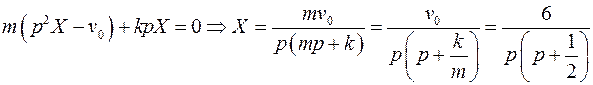
Здесь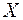 
- изображение функции 
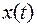. Оригинал находится как сумма вычетов функции
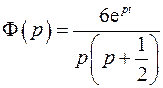
Особые точки – нули знаменателя:
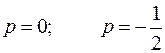
Очевидно, это полюсы первого порядка. Найдем вычеты в особых точках:
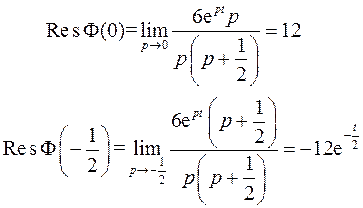
Получим:
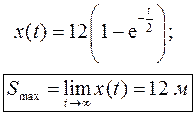
3.14. Решить систему дифференциальных уравнений:
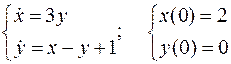
Ищем решение операционным методом.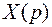 
и 
- и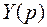зображения функци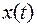й и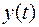 
. Изображение единичной функции найдено выше (см. п. 3.23.) и равно 
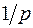. Получим:
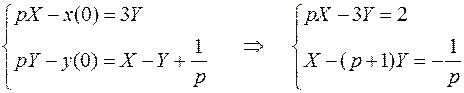
Получена система линейных алгебраических уравнений относительно изображени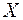й и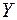 
. Ее определитель:
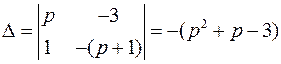
Найдем определител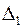и 
и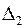 
, а затем - 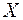и :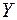
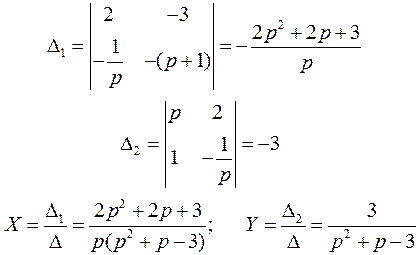
Найдем оригиналы 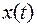и 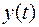как сумму вычетов функций
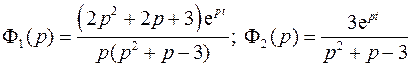
Найдем корни уравнения:
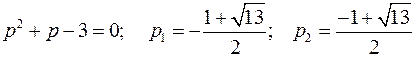
Можно записать
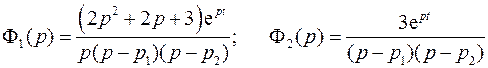
Особые точки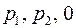 
(последняя – только для функции 
) – полюсы первого порядка. Найдем вычеты и оригиналы:
1).
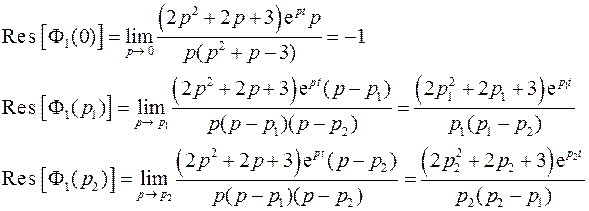
Получим:
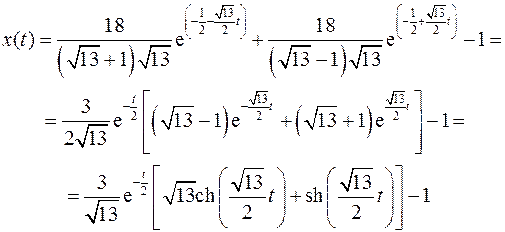
2).
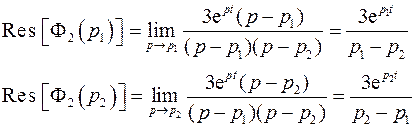
Получим:
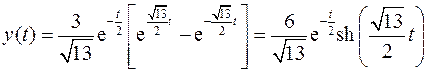
Окончательно:
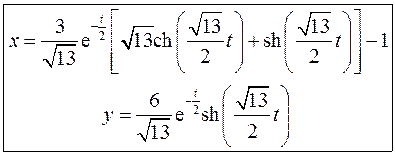
3.15. Выяснить, во что преобразуется геометрическая фигура при отображении функцией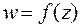 
: 
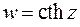; полоса 
.
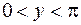Построим исходную фигуру (полосу):
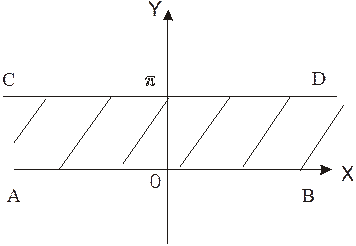
Полоса ограничена прямым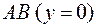и 
и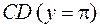 
; абсциссы точек 
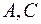определяются как 
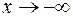, а абсциссы точек 
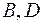- как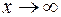 
. Запишем отображение
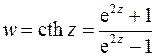
Найдем линию, в которую отображается граничная прямая . На этой прямой 
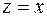. Получим:
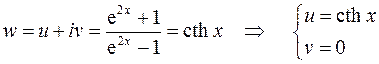
- часть оси абсцисс на плоскости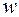 
.
Определим, куда отображаются точки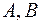 
1) точка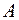 
:
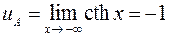
2) точка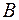 
:
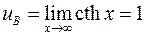
Так как прямая 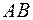непрерывна, то возможны два случая:
1) 
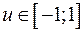
2) 
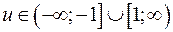
Чтобы выяснить, какая именно возможность реализуется, определим, во что отображается точка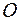 
:
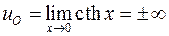
Таким образом,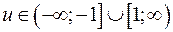
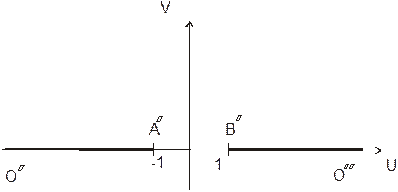
Найдем линию, в которую отображается вторая граничная прямая -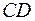 
. Ее уравнение 
.
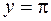Получим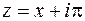 
и далее:
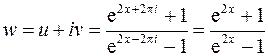
Учтено, что:
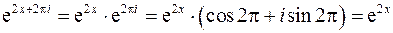
Получили то же самое отображение, что и в предыдущем случае:
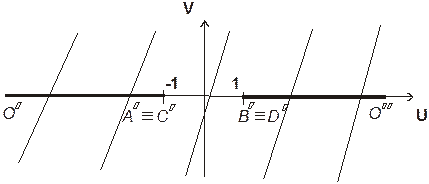
Таким образом, отображение – это вся комплексная плоскость с разрезами вдоль оси абсцисс:
1) 
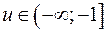2) 
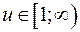
Основная литература
1. Лавит И.М. Конспект лекций дисциплины «Комплексный анализ». 2012. (ресурс кафедры).
Дополнительная литература
1. Привалов И.И. Введение в теорию функций комплексного переменного: учебник / И.И. Привалов .— 15-е изд., стер .— СПб. ; М. ; Краснодар : Лань, 2009 .— 432 с. (1 экз.)
2. Рудкевич, Е.А. Методические указания к решению задач по теме "Функции комплексного переменного" / Е.А.Рудкевич; ТулГУ .— Тула, 2003 .— 49 с. (1 экз.)
3. Рудкевич, Е.А. Функции комплексного переменного и операционное исчисление (методы решения задач : учебное пособие / Е.А.Рудкевич;ТулГУ .— Тула, 2004 .— 64 с. (1 экз.)
4. Лунц Г.Л. Функции комплексного переменного с элементами операционного исчисления: учебник для вузов / Г.Л.Лунц, Л.Э.Эльсгольц. — 3-е изд. — СПб.: Лань, 2006. — 304 с. (5 экз.)
5. Лаврентьев М.А. Методы теории функций комплексного переменного / М.А.Лаврентьев, Б.В.Шабат. — 7-е изд., стер. — М.: Лань, 2007. — 688 с. (10 экз.)
Рассмотрено на заседании кафедры
Протокол №_____ от "___" ______________ 2012 г.
Зав. кафедрой ____________________ А.А. Маркин