Билеты по информатике. Герасимов И.В. I семестр.

Дата: 2025-04-30; Просмотры: 4
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

1. Объекты информации, сообщения, процессы. Объяснить суть

объекта информации (энтропия).

  1. Понятие сигнала (передача символа).
  2. Формализованное представление информации. Слова в двоичном алфавите. (Бит). 1 бит – равновероятность и неопределенность.
  3. Кодирование информации (в ОС) (взаимнооднозначное соответствие), установление в ОС – суть кодирования (ASCII)
  4. Канал передачи данных без помех (кодер, декодер).
  5. Оценка количества информации в сообщении.
  6. Числовая интерпретация двоичного слова
  7. Логическая интерпретация двоичного слова (интерпретация с помощью множества). Представление множеств двоичными словами.
  8. Метод компьютерного моделирования как основной метод информатики. Схема метода.
  9. Знаковые системы: физические, лингвистические, логические, иконические.
  10. Взаимодействующие аспекты знака: синтаксический, семантический, прагматический.
  11. Основное назначение ОС. ОС как модель РС для юзера.
  12. Основные функции операционной системы.
  13. Организация данных и управление ими. Понятие файловой системы (БД).
  14. Архитектура компьютера по фон Нейману.
  15. Модель открытой информационной системы. Общая характеристика корпоративной сети ETUNET.
  16. Сервер сети. Назначение, виды, архитектура, основные функции.
  17. Способы доступа к ресурсам сервера.
  18. Клиент сети. Назначение, основные функции, организация доступа к ресурсам сети.
  19. Задачи поиска информации: цель поиска, формирование задания на поиск, сохранение результатов поиска.
  20. Текстовое представление информации. Двоичные слова и их интерпретация.
  21. Текстовые редакторы.
  22. Нелинейная организация текста (гипертекст).
  23. Алгоритмическое представление информации.
  24. Высказывание. Структура логики высказывания.
  25. Сведение вычислений к физическим процессам. Интерпретация законов логики в предметной области вычислительной техники.
  26. Гипотеза о физической символьной системе.
  27. Абстрактная вычислительная машина Тьюринга.

 

1. Объекты информации, сообщения, процессы. Объяснить суть

объекта информации (энтропия).

 

Термин «информация» настолько дискуссионен, что до сих пор, несмотря на многочисленные научные работы в области информатики и естественных наук, посвящённые информации, не существует общепринятого определения. Методологической платформой для определения сущности информации является многоаспектность этого феномена. Основа для такого подхода – рассмотрение единого информационного процесса, разные стадии которого как раз и порождают множество определений, ибо на каждой отдельной стадии информация проявляет свои специфические черты. В этой связи уместно сопоставить развитие кибернетики и становление синергетики.

Отличительные особенности кибернетики и синергетики:

1. Кибернетика изучает законы управления и связи, оперируя законами управления и информационными взаимодействиями (с помощью обратных связей) на нескольких уровнях одновременно. Синергетика имеет дело с системами неуправляемыми, их развитие можно только направлять, при этом небольшое энергетическое воздействие в нужной пространственно-временной точке оказывается достаточным, чтобы система перестроилась, и возник новый тип структур.

2. Кибернетика использует информацию как нечто данное. Выяснение причин и механизмов её возникновения не входит в её задачи. С позиции синергетики для генерации информации принципиально важны хаотические состояния систем, выход из которых сопровождается созданием информации.

У каждого человека существует интуитивное представление об информации как о совокупности содержательных сведений, заключённых в том или ином сообщении. В качестве сообщения может фигурировать, например, текст учебного пособия, и т. д. Вкладывая в это понятие аналогичный смысл, можно говорить об информации, хранящейся в памяти компьютера, или о генетической информации, закодированной в хромосомах живого организма. Информация – важнейший элемент, без которого невозможен ни один процесс управления в технической системе, живом организме или человеческом обществе.

Но это не означает, что информация присутствует всюду. Представление об информации должно быть связано с понятием процесса.

Необходимо отметить, что процесс генерации информации не имеет аналогов в естественных науках. Это – событие, объединяющее «случай» и «необходимость», поскольку случайный выбор в момент генерации возможен только из числа состояний, разрешённых природой.

Любая информация обрабатывается компами для достижения некоторых целей, и мы оцениваем интеллектуальность системы по её способности достигать заявленных целей в условиях изменчивости, трудности и сложности, порождаемых характером поставленных задач.

Одно из необходимых свойств интеллектуального поведения – способность хранить и передавать символы, а так же манипулировать ими. Информация – потребляемый всеми отраслями народного хозяйства ресурс, имеющий для них такое же значение, как энергетические ресурсы или запасы полезных ископаемых. Причем с развитием общества организация использования информационных ресурсов, в которых обобщаются и концентрируются все имеющиеся сведения (данные, факты, знания) о различных вопросах экономики, науки, техники, технологии, культуры, искусства, медицины и т.д., оказываются все большее влияния на интеллектуальную и экономическую жизнь. Информация – совокупность научно-технических сведений, фактов, знаний о результатах развития науки и техники. Другими словами, информация является продуктом и «сырьем» системы информационного обслуживания научно-технической деятельности. Информация – сумма продуктов, формируемых в системах информационного обслуживания научно-технической деятельности и подготовки кадров различных профилей, т.е. область производства и потребления информационных ресурсов ограничивается лишь интеллектуальной жизнью общества.

2. Понятие сигнала (передача символа).

Для передачи сообщения на далекие расстояния их преобразуют в соответствующий электрический или оптический сигнал. Как говорят, кодируют сообщения. В случае электрического сигнала формируется процесс u(t), характеризуемый определенной зависимостью электрической величины u от времени t. Звуки, например, сравнительно просто кодируются микрофонным устройством. Роль сообщения играет звуковое давление p на мембрану микрофона, изменяющееся во времени по закону p(t). При этом в угольном микрофоне соответствующим образом изменяется сопротивление микрофона и ток в его цепи. В результате на выходе микрофонного устройства напряжение u(t) изменяется во времени по тому же закону, что и звуковое давление p(t).

При изучении сигнала с точки зрения передаваемой информации несущественно, какая именно электрическая (оптическая) величина подразумевается под u – напряжение, ток или заряд. Важно не что изменяется, а как изменяется эта величина во времени. Можно отвлечься от физической природы этой величины и интересоваться характером абстрактной математической зависимости u(t), т.е. функции времени t. В конечном итоге, для нас важно, что независимо орт физической природы сообщения кодирующий его сигнал передается в виде определенной функции времени.

Представление сигнала.

Изучая некоторое событие мы обычно интересуемся тем, где и когда оно произошло, какие перемещения в пространстве и изменения во времени имели место. Поэтому мы привыкли рассматривать большинство величин как функции пространственных координат и времени. Так возникает понятие поля.

При рассмотрении электромагнитных сигналов пространственные координаты источника сигнала (приемника) во внимание как правило, не принимаются (напомним, что в воздухе скорость электромагнитной волны приблизительно 3*108 м/с). Электромагнитные волны распространяются примерно в миллион раз быстрее звуковых именно в зависимости u(t).

Эту зависимость можно записать в виде формулы (аналитически) или представить в виде графика u(t), но можно сигнал охарактеризовать по-другому, с точки зрения его спектрального состава, и тоже представить графически соответствующим образом.

Будем рассматривать, главным образом, такие сигналы, которые являются периодическими, т.е. функция u(t) удовлетворяет соотношению u(t+nT)=u(t), где T – постоянная величина, называемая периодом; n – любое целое число, периодический процесс можно охарактеризовать также частотой v=1/T.

Теоретически предполагается, что такая периодичность длится вечно и не имеет начала и конца во времени. Практически периодическим процессом относят такие процессы, длительность которых намного больше периода.

У них одинаковая частота, но различная форма колебаний. Эти различные формы имеют разный спектральный состав.

Спектры звуков

Звуковые сообщения обычно подразделяются на музыкальные звуки и шумы.

Музыкальный звук представляет собой периодически изменяющийся процесс. В частности если этот процесс гармонический говорят о музыкальном тоне.В спектре соответствующего сигнала наибольшую амплитуду имеет основной тон с ростом номера гармоник амплитуда их заметно падает. Так что практически спектр музыкального тона имеет немного гармоник. Гармоники определяют тембр музыкальных звуков. Одинаковые ноты разных инструментов имеют разное число гармоник и разные соотношения между их амплитудами. Значит и их спектры различны (благодаря этому наше ухо определяет инструмент). Отрывистые звуки (удар барабана) являются шумами. Сигналы шумов отличаются не периодичностью и сложной зависимостью от времени. Спектр шума значительно шире и богаче спектра музыкальных тонов. Качественное отличие различных шумов выражается в том, что спектр одного шума может иметь более интенсивные спектральные компоненты в области низких частот, а другого шума – на более высоких частотах т.е. различных пропорциях между спектральными компонентами. Спектральные представления позволяют создать единый и наглядный язык для написания процессов различной физической природы, использовать подчас неожиданные ассоциации и аналогии. Специалисты иногда используют термин белый шум – это такой шум, в сплошном спектре которого присутствуют все звуковые частоты, причем различные спектральные компоненты отличаются по энергии не очень сильно.

Спектры импульсных сигналов

В современной вычислительной технике и технике связи часто используются сигналы в виде периодически повторяющихся импульсов прямоугольной формы. Такие импульсы имеют богатый спектр, содержащий много спектральных линий, сгруппированных в своеобразные «лепестки», причем частоты, соответствующие «узлам» этих лепестков, равны n/ τ, где n- номер лепестка. Теоретически подобные спектры имеют бесконечную протяженность по частоте, но поскольку после третьего лепестка амплитуды гармоник становятся пренебрежимо малыми практически можно ограничится первыми тремя лепестками. Ширина такого ограниченного спектра ∆v связана с длительностью импульса τ простой зависимостью: ∆v=3/ τ, т.е. ширина спектра прямоугольного импульса обратно пропорциональна его длительности.

Это соотношение имеет большое практическое значение. Оно показывает, что чем меньше длительность импульсов, т. е. Чем меньше занимается линия связи, тем более широким является спектр такого сигнала и тем более широкая полоса частот требуется для достаточно правильного его воспроизведения.

На примере прямоугольных импульсов мы рассмотрели весьма любопытную закономерность, справедливую и для других видов импульсов. Эту закономерность можно выразить математически, переписав приведенное выше соотношение в виде τ∆v=const. Физический смысл этого соотношения состоит в том, что невозможно одновременно сконцентрировать такой сигнал во времени и по частотам.

Из приведенной выше формулы также следует, что ширина спектра ∆v прямоугольных импульсов определяется их длительностью τ и не зависит от частоты повторения импульсов v=1/T. Это важно практически, т.к. позволяет легко определить минимальное значение τ, при котором полоса частот, занимаемая данным сигналом, не превысит допустимую для данной системы передачи и приема импульсных сигналов.

Однако с изменением частоты v изменяется число спектральных линий в каждом лепестке, т.е. их густота. Очевидно, в предельном случае перехода от периодически повторяющихся импульсов к одиночному импульсу (T→ ∞ и v→0) спектр должен стать сплошным.

Спектральные представления универсальны. Спектры самым тесным образом связаны с формой и длительностью соответствующих процессов и сигналов. Спектральные представления позволяют сравнивать разные объекты информации (музыка, речь, изображения и др.) с единых позиций, определять ширину спектра кодирующих их сигналов и на основании этого судить о возможности передачи этих сигналов по тем или иным линиям связи.

 

 

3.Формализованное представление Информ. Слова в |2| алфавите.

Применительно к теории информации во внимание принимается только синтаксическая компонента объекта информации (артефакта), две другие (семантическая и прагматическая) в классической теории информации не рассматриваются. В качестве конкретного объекта информации в данном случае можно рассмотреть число (абстрактный тип данных, который применительно к конкретной машине имеет конкретное представление). Будем рассматривать двоичное представление. <буква>:={1,0}; <слово>:=<буква>|…|<буква>. Т.е. любое слово (число) в двоичном алфавите выглядит как последовательность 0 и 1.

4 . Кодирование информации.

Рассмотрим кодировании информации на примере представления множества положительных чисел . Для представления числа 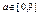необходимо иметь 3хбуквенное слово, тогда возможно взаимно однозначное соответствие м/у числами упомянутого множества и двоичными словами: 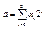, где ai – буква двоичного алфавита. Представленный пример оформления неотрицательных чисел в виде двоичного слова иллюстрирует процедуру кодирования информации. Если рассматривать числа 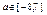необходимо использовать двоичные слова не менее чем из 4х букв. При определении процедуры кодирования для этого случая принципы взаимнооднозначного соответствия учитываются. Требуется использование одного и того же физического устройства для выполнения как операция сложения так для операций вычитания с использованием таблицы:

X1 X2 X1ÅX2
0 0 0
1 0 1
0 1 1
1 1 0

 

5. Канал передачи данных без помех (кодер, декодер).

Передача сообщения от источника к приёмнику всегда связана с некоторым нестационарным процессом, происходящим в материальной среде – это условие является обязательным, поскольку сама информация материальным объектом или формой существования не является. Способов передачи информации существует множество: почта, телефон, комп. сети и пр. Обобщённая схема передачи информации:

Любой реальный канал связи подвержен внешним воздействиям, а так же в нём могут происходить внутренние процессы, в результате которых искажаются передаваемые сигналы и, следовательно, связанное с ними сообщение. Такие воздействия называются шумами (помехами).

Основной характеристикой каналов передачи информации является их пропускная способность (скорость передачи информации). Пропускная способность канала равна количеству информации, которое может передаваться по нему в единицу времени. Применительно к каналу данных без помех возникают 3 главных вопроса:

1. Какова пропускная способность канала? Оценивается кол-во букв из двоичного алфавита, передаваемых в секунду.

2. Можно ли полностью использовать пропускную способность канала при передаче сообщения в алфавите источника?

3. Как осуществить процедуру кодирования так, чтобы получить максимальную пропускную способность канала передачи данных?

Простейшим вариантом протокола передачи данных является синхронный, при котором время, отводимое на 1 символ, является неизменным ( 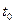). В таком случае пропускная способность канала определяется так: 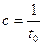. Если же с передачей одного импульса связано кол-во информации 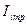, то .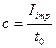

Процедура оптимального кодирования.

А. Вариант установления соответствия.

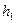
0
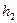
1
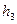
01
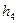
10

В таком случае взаимнооднозначное соответствие для букв есть, но применительно к декодированию возникает проблема: существуют коды (0,1), (1,0), началом которых являются коды для предыдущих букв.

Б. Решение проблемы.

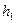
00
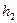
01
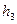
10
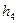
11

Но при таком кодировании не обеспечивается максимальная пропускная способность канала.

Задано исходное множество букв и гистограмма, характеризующая вероятности появления этих букв.

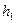
0,5
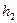
0,25
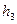
0,125
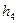
0,125

В основу построения оптимального кода положено требование равной частоты появления букв 0, 1 в двоичном слове, передаваемом по каналу передачи данных. Это требовании обеспечивается в помощью след. процедуры.

Исходное множество распадается на 2 подмножества так, что осуществляется баланс вероятности.

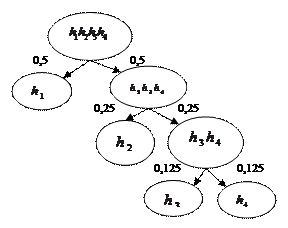Тогда в первой позиции:

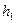
0
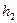
1
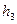
1
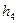
1

 

Во второй позиции:

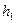
0
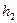
10
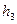
11
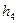
11

В третьей позиции:

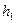
0
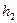
10
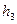
110
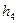
111

Таким образом, баланс вероятности выполняется.

Суть первой теоремы Шеннона состоит только в установлении факта существования кода, наилучшего по пропускной способности канала. Собственно процедура кодирования Шенноном не рассматривается.

 

 

6. Оценка количества информации в сообщении.

Информация – получение информации это снятие неопределенности.

Количество информации в 1 бит мы получаем при проведении опыта в результате опыта с двумя равновероятными исходами.

Количество информации, полученное в результате проведения опыта с N-равновероятными исходами равно:

I=log 2 (N).

[I]=[1 бит]. Бит – это количество информации, снимающее неопределенность в одном опыте с двумя равновероятными исходами.

Пусть имеем множество из М элементов. Это множество может представлять собой ансамбль сигналов или алфавит канала передачи данных. При получении сообщения из N элементов мы получаем количество информации (при условии равновероятности появления каждого элемента):

I=N*log 2(M).

I= - N*log 2(P).

Очевидно, что вероятность появления буквы: Р=1/M.

Эта мера количества информации называется мерой Хартли.

В условиях, когда появление следующего символа неравновероятно, количество информации, несомое одной буквой, больше, если вероятность ее появления меньше. И наоборот. Среднее количество информации, несомое одной буквой:

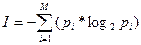
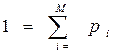
Пример 1:

Рассмотрим крайний случай, когда мы точно знаем, что следующий символ будет именно таким: то есть Р=1:

I~log2 (1)=0.

Пример 2:

Пусть имеем опыт с двумя неравновероятными исходами (взаимоисключающими), то есть: 1=Р1+Р2

I=-P1log2(P1)-(1-P1)log2(1-P1)

График этой функции приведен ниже:

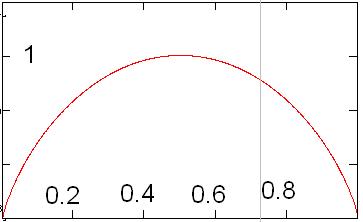
Смысл его в том, что среднее количество информации, приходящееся на одну переданную/полученную букву максимален в том и только том случае, когда появление букв этого алфавита равновероятно. Частный случай, когда вероятность появления одной из букв стремится к нулю (единице), среднее количество информации на принятый символ стремится к нулю, что иллюстрируется примером.

 

7. Числовая интерпретация двоичного слова.

Пусть имеем некоторое множество натуральных чисел (для примера):

Порядок элементов множества не важен. Нам нужно сопоставить каждому элементу этого множества некоторое двоичное слово. Очевидно, что нам понадобится слово длиной не менее 4 букв (двоичных). Также очевидно, что правил соответствия будет N!, где N – количество элементов множества. Одно из правил соответствия называется двоичная позиционная система счисления. Число в любой позиционной системе счисления в десятичную переводится по формуле:

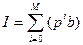
Где р – основание системы счисления, соответственно b – цифра, а i – позиция данной цифры в слове (числе).

Тогда получаем взаимнооднозначное соответствие между элементами исходного множества и двоичными словами.

Но данное правило не единственно!

Существует также так называемый дополнительный код числа.

Разряд слова с наибольшим номером определяет знак числа: реально получаем, что в дополнительном коде вес цифры в этом разряде равен I=-bi, где i – номер позиции, а b – цифра в данной позиции.

Пример 1:

1=0001

7=0111

-7=1001

то есть дополнительный код получается(ДК) по правилу:

1. Инвертирование (то есть замена 1 на 0 и 0 на1) каждого бита прямого кода числа.

2. Добавление к полученному единицы.

Смысл введения ДК заключается в упрощении реализации арифметических операций с положительными и отрицательными числами, так как можно использовать одно устройство (сумматор двоичных чисел) для вычитания и сложения. В самом деле

7 0111
-7 1001
0 0000