6. Какие статистики характеризуют качество построенной модели?
7. Что такое анализ переменной Resid? Зачем он необходим?
8. Что такое гетероскедастичность? Какие тесты позволяют провести проверку и устранить гетероскедастичности?
9. Как в среде EView использовать обобщенный МНК.
Лабораторная работа № 3
В соответствии с данными лабораторной работы № 1, используя программу EViews, необходимо выполнить следующие задания:
1) для характеристики зависимости между выбранными переменными рассчитать параметры следующих функций:
линейной y = a + bx,
степенной y = axb,
показательной y = abx,
логарифмической y = a + blnx,
равносторонней гиперболы y = a + 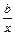 ,
,
квадратичной y = a + bx2,
полиномиальной y = a + b1x + b2x2;
2) оценить каждую модель через показатель детерминации,
F-критерий Фишера и выбрать наилучшую из них.
Контрольные вопросы
1. Что такое нелинейная регрессия?
2. Какие классы нелинейных регрессий вы знаете? Приведите примеры.
3. Метод наименьших квадратов для нелинейных регрессий.
4. Интерпретация коэффициентов регрессии для нелинейных моделей.
5. Оценка адекватности нелинейных моделей.
Лабораторная работа № 4
В соответствии со своим вариантом в работе необходимо выполнить следующие задания:
1) найти описательные статистики переменных и сделать вывод о выборке наблюдений;
2) построить линейное уравнение множественной регрессии и пояснить экономический смысл его параметров;
3) рассчитать частные коэффициенты эластичности, а также стандартизированные коэффициенты регрессии; сделать вывод о силе связи результата и фактора;
4) рассчитать парные, частные коэффициенты корреляции, а также множественный коэффициент корреляции; сделать выводы;
5) проверить значимость уравнения регрессии на 5%-м уровне по
F-критерию, проверить значимость коэффициентов регрессии по
t-статистике;
6) рассчитать прогнозное значение результата, если прогнозное значение факторов составляют 80% от их максимальных значений;
7) проверить остатки на гетероскедастичность с помощью теста Уайта; если необходимо, применить взвешенный метод наименьших квадратов, сделать выводы.
Вариант 1. По данным, представленным в табл. 30, изучается зависимость чистого дохода у (млрд долл.) крупнейших компаний США в 20ХХ г. от оборота капитала х1 (млрд долл.) и использованного капитала х2 (млрд долл.).
Таблица 30
| № п/п | y | x 1 | x 2 | № п/п | y | x 1 | x 2 |
| 1 | 0,9 | 31,3 | 18,9 | 14 | 1,4 | 9,8 | 12,6 |
| 2 | 1,7 | 13,4 | 13,7 | 15 | 0,4 | 19,5 | 12,2 |
| 3 | 0,7 | 4,5 | 18,5 | 16 | 0,8 | 6,8 | 3,2 |
| 4 | 1,7 | 10,0 | 4,8 | 17 | 1,8 | 27,0 | 13,0 |
| 5 | 2,6 | 20,0 | 21,8 | 18 | 0,9 | 12,4 | 6,9 |
| 6 | 1,3 | 15,0 | 5,8 | 19 | 1,1 | 17,7 | 15,0 |
| 7 | 4,1 | 137,0 | 99,0 | 20 | 1,9 | 12,7 | 11,9 |
| 8 | 1,6 | 17,9 | 20,1 | 21 | -0,9 | 21,4 | 1,6 |
| 9 | 6,9 | 165,0 | 60,6 | 22 | 1,3 | 13,5 | 8,6 |
| 10 | 0,4 | 2,0 | 1,4 | 23 | 2,0 | 13,4 | 11,5 |
| 11 | 1,3 | 6,8 | 8,0 | 24 | 0,6 | 4,2 | 1,9 |
| 12 | 1,9 | 27,1 | 18,9 | 25 | 0,7 | 15,5 | 5,8 |
| 13 | 1,9 | 13,4 | 13,2 |
Табличные значения статистик: t0,95; 22 = 2,07; F0,05;2;22 = 3,44.
Вариант 2. По данным, представленным в табл. 31, изучается зависимость чистого дохода у (млрд долл.) крупнейших компаний США в 20ХХ г. от оборота капитала х1 (млрд долл.) и численности служащих х2 (тыс. чел.).
Таблица 31
| № п/п | y | x 1 | x 2 | № п/п | y | x 1 | x 2 |
| 1 | 0,9 | 31,3 | 43,0 | 14 | 1,4 | 9,8 | 212,0 |
| 2 | 1,7 | 13,4 | 64,7 | 15 | 0,4 | 19,5 | 105,0 |
| 3 | 0,7 | 4,5 | 24,0 | 16 | 0,8 | 6,8 | 33,5 |
| 4 | 1,7 | 10,0 | 50,2 | 17 | 1,8 | 27,0 | 142,0 |
| 5 | 2,6 | 20,0 | 106 | 18 | 0,9 | 12,4 | 96,0 |
| 6 | 1,3 | 15,0 | 96,6 | 19 | 1,1 | 17,7 | 140,0 |
| 7 | 4,1 | 137,0 | 347 | 20 | 1,9 | 12,7 | 59,3 |
| 8 | 1,6 | 17,9 | 85,6 | 21 | -0,9 | 21,4 | 131,0 |
| 9 | 6,9 | 165,0 | 745,0 | 22 | 1,3 | 13,5 | 70,7 |
| 10 | 0,4 | 2,0 | 4,1 | 23 | 2,0 | 13,4 | 65,4 |
| 11 | 1,3 | 6,8 | 26,8 | 24 | 0,6 | 4,2 | 23,1 |
| 12 | 1,9 | 27,1 | 42,7 | 25 | 0,7 | 15,5 | 80,8 |
| 13 | 1,9 | 13,4 | 61,8 |
Табличные значения статистик: t0,95; 22 = 2,07; F0,05;2;22 = 3,44.
Вариант 3. По данным, представленным в табл. 32, изучается зависимость чистого дохода у (млрд долл.) крупнейших компаний США в 20ХХ г. от оборота капитала х1 (млрд долл.) и рыночной капитализацией компании х2 (млрд долл.).
Таблица 32
| № п/п | y | x 1 | x 2 | № п/п | y | x 1 | x 2 |
| 1 | 0,9 | 31,3 | 40,9 | 14 | 1,4 | 9,8 | 33,1 |
| 2 | 1,7 | 13,4 | 40,5 | 15 | 0,4 | 19,5 | 32,7 |
| 3 | 0,7 | 4,5 | 38,9 | 16 | 0,8 | 6,8 | 32,1 |
| 4 | 1,7 | 10,0 | 38,5 | 17 | 1,8 | 27,0 | 30,5 |
| 5 | 2,6 | 20,0 | 37,3 | 18 | 0,9 | 12,4 | 29,8 |
| 6 | 1,3 | 15,0 | 26,5 | 19 | 1,1 | 17,7 | 25,4 |
| 7 | 4,1 | 137,0 | 37,0 | 20 | 1,9 | 12,7 | 29,3 |
| 8 | 1,6 | 17,9 | 36,8 | 21 | -0,9 | 21,4 | 29,2 |
| 9 | 6,9 | 165,0 | 36,3 | 22 | 1,3 | 13,5 | 29,2 |
| 10 | 0,4 | 2,0 | 35,3 | 23 | 2,0 | 13,4 | 29,1 |
| 11 | 1,3 | 6,8 | 35,3 | 24 | 0,6 | 4,2 | 27,9 |
| 12 | 1,9 | 27,1 | 35,0 | 25 | 0,7 | 15,5 | 27,2 |
| 13 | 1,9 | 13,4 | 26,2 |
Табличные значения статистик: t0,95; 22 = 2,07; F0,05;2;22 = 3,44.
Вариант 4. По данным, представленным в табл. 33, изучается зависимость чистого дохода у (млрд долл.) крупнейших компаний США в 20ХХ г. от использованного капитала х1 (млрд долл.) и численности служащих х2 (тыс. чел.).
Таблица 33
| № п/п | y | x 1 | x 2 | № п/п | y | x 1 | x 2 |
| 1 | 0,9 | 18,9 | 43,0 | 14 | 1,4 | 12,6 | 212,0 |
| 2 | 1,7 | 13,7 | 64,7 | 15 | 0,4 | 12,2 | 105,0 |
| 3 | 0,7 | 18,5 | 24,0 | 16 | 0,8 | 3,2 | 33,5 |
| 4 | 1,7 | 4,8 | 50,2 | 17 | 1,8 | 13,0 | 142,0 |
| 5 | 2,6 | 21,8 | 106 | 18 | 0,9 | 6,9 | 96,0 |
| 6 | 1,3 | 5,8 | 96,6 | 19 | 1,1 | 15,0 | 140,0 |
| 7 | 4,1 | 99,0 | 347 | 20 | 1,9 | 11,9 | 59,3 |
| 8 | 1,6 | 20,1 | 85,6 | 21 | -0,9 | 1,6 | 131,0 |
| 9 | 6,9 | 60,6 | 745,0 | 22 | 1,3 | 8,6 | 70,7 |
| 10 | 0,4 | 1,4 | 4,1 | 23 | 2,0 | 11,5 | 65,4 |
| 11 | 1,3 | 8,0 | 26,8 | 24 | 0,6 | 1,9 | 23,1 |
| 12 | 1,9 | 18,9 | 42,7 | 25 | 0,7 | 5,8 | 80,8 |
| 13 | 1,9 | 13,2 | 61,8 |
Табличные значения статистик: t0,95; 22 = 2,07; F0,05;2;22 = 3,44.
Вариант 5. По данным, представленным в табл. 34, изучается зависимость чистого дохода у (млрд долл.) крупнейших компаний США в 20ХХ г. от использованного капитала х1 (млрд долл.) и рыночной капитализации компании х2 (млрд долл.).
Таблица 34
| № п/п | y | x 1 | x 2 | № п/п | y | x 1 | x 2 |
| 1 | 0,9 | 18,9 | 40,9 | 14 | 1,4 | 12,6 | 33,1 |
| 2 | 1,7 | 13,7 | 40,5 | 15 | 0,4 | 12,2 | 32,7 |
| 3 | 0,7 | 18,5 | 38,9 | 16 | 0,8 | 3,2 | 32,1 |
| 4 | 1,7 | 4,8 | 38,5 | 17 | 1,8 | 13,0 | 30,5 |
| 5 | 2,6 | 21,8 | 37,3 | 18 | 0,9 | 6,9 | 29,8 |
| 6 | 1,3 | 5,8 | 26,5 | 19 | 1,1 | 15,0 | 25,4 |
| 7 | 4,1 | 99,0 | 37,0 | 20 | 1,9 | 11,9 | 29,3 |
| 8 | 1,6 | 20,1 | 36,8 | 21 | -0,9 | 1,6 | 29,2 |
| 9 | 6,9 | 60,6 | 36,3 | 22 | 1,3 | 8,6 | 29,2 |
| 10 | 0,4 | 1,4 | 35,3 | 23 | 2,0 | 11,5 | 29,1 |
| 11 | 1,3 | 8,0 | 35,3 | 24 | 0,6 | 1,9 | 27,9 |
| 12 | 1,9 | 18,9 | 35,0 | 25 | 0,7 | 5,8 | 27,2 |
| 13 | 1,9 | 13,2 | 26,2 |
Табличные значения статистик: t0,95; 22 = 2,07; F0,05;2;22 = 3,44.
Вариант 6. По данным, представленным в табл. 35, изучается зависимость чистого дохода у (млрд долл.) крупнейших компаний США в 20ХХ г. от численности служащих х1 (тыс. чел.) и рыночной капитализации компании х2 (млрд долл.).
Таблица 35
| № п/п | y | x 1 | x 2 | № п/п | y | x 1 | x 2 |
| 1 | 0,9 | 18,9 | 43,0 | 14 | 1,4 | 12,6 | 212,0 |
| 2 | 1,7 | 13,7 | 64,7 | 15 | 0,4 | 12,2 | 105,0 |
| 3 | 0,7 | 18,5 | 24,0 | 16 | 0,8 | 3,2 | 33,5 |
| 4 | 1,7 | 4,8 | 50,2 | 17 | 1,8 | 13,0 | 142,0 |
| 5 | 2,6 | 21,8 | 106 | 18 | 0,9 | 6,9 | 96,0 |
| 6 | 1,3 | 5,8 | 96,6 | 19 | 1,1 | 15,0 | 140,0 |
| 7 | 4,1 | 99,0 | 347 | 20 | 1,9 | 11,9 | 59,3 |
| 8 | 1,6 | 20,1 | 85,6 | 21 | -0,9 | 1,6 | 131,0 |
| 9 | 6,9 | 60,6 | 745,0 | 22 | 1,3 | 8,6 | 70,7 |
| 10 | 0,4 | 1,4 | 4,1 | 23 | 2,0 | 11,5 | 65,4 |
| 11 | 1,3 | 8,0 | 26,8 | 24 | 0,6 | 1,9 | 23,1 |
| 12 | 1,9 | 18,9 | 42,7 | 25 | 0,7 | 5,8 | 80,8 |
| 13 | 1,9 | 13,2 | 61,8 |
Табличные значения статистик: t0,95; 22 = 2,07; F0,05;2;22 = 3,44.
Вариант 7. По данным, представленным в табл. 36, изучается зависимость индекса человеческого развития у 25 стран от расходов на конечное потребление в текущих ценах х1 (% к ВВП) и валового накопления х2 (% к ВВП).
Таблица 36
| № п/п | y | x 1 | x 2 | № п/п | y | x 1 | x 2 |
| 1 | 0,904 | 75,5 | 25,2 | 14 | 0,744 | 90,2 | 23,0 |
| 2 | 0,922 | 78,5 | 21,8 | 15 | 0,921 | 72,8 | 20,2 |
| 3 | 0,763 | 78,4 | 25,7 | 16 | 0,927 | 67,7 | 25,2 |
| 4 | 0,923 | 77,7 | 17,8 | 17 | 0,802 | 82,6 | 22,4 |
| 5 | 0,918 | 84,4 | 15,9 | 18 | 0,747 | 74,4 | 22,7 |
| 6 | 0,906 | 75,9 | 22,4 | 19 | 0,927 | 83,3 | 18,1 |
| 7 | 0,905 | 76,0 | 20,6 | 20 | 0,721 | 83,7 | 20,1 |
| 8 | 0,545 | 67,5 | 25,2 | 21 | 0,913 | 73,8 | 17,3 |
| 9 | 0,894 | 78,2 | 20,7 | 22 | 0,918 | 79,2 | 16,8 |
| 10 | 0,900 | 78,1 | 17,5 | 23 | 0,833 | 71,5 | 29,9 |
| 11 | 0,932 | 78,6 | 19,7 | 24 | 0,914 | 75,3 | 20,3 |
| 12 | 0,740 | 84,0 | 18,5 | 25 | 0,923 | 79,0 | 14,1 |
| 13 | 0,701 | 56,2 | 42,4 |
Табличные значения статистик: t0,95; 22 = 2,07; F0,05;2;22 = 3,44.
Вариант 8. По данным, представленным в табл. 37, изучается зависимость индекса человеческого развития у 25 стран от ВВП 20ХХ г. х1 (% к 20ХХ г.) и валового накопления х2 (% к ВВП).
Таблица 37
| № п/п | y | x 1 | x 2 | № п/п | y | x 1 | x 2 |
| 1 | 0,904 | 115 | 25,2 | 14 | 0,744 | 94 | 23,0 |
| 2 | 0,922 | 123 | 21,8 | 15 | 0,921 | 118 | 20,2 |
| 3 | 0,763 | 74 | 25,7 | 16 | 0,927 | 130 | 25,2 |
| 4 | 0,923 | 111 | 17,8 | 17 | 0,802 | 127 | 22,4 |
| 5 | 0,918 | 113 | 15,9 | 18 | 0,747 | 61 | 22,7 |
| 6 | 0,906 | 110 | 22,4 | 19 | 0,927 | 117 | 18,1 |
| 7 | 0,905 | 119 | 20,6 | 20 | 0,721 | 46 | 20,1 |
| 8 | 0,545 | 146 | 25,2 | 21 | 0,913 | 107 | 17,3 |
| 9 | 0,894 | 113 | 20,7 | 22 | 0,918 | 110 | 16,8 |
| 10 | 0,900 | 108 | 17,5 | 23 | 0,833 | 99,2 | 29,9 |
| 11 | 0,932 | 113 | 19,7 | 24 | 0,914 | 101 | 20,3 |
| 12 | 0,740 | 71 | 18,5 | 25 | 0,923 | 105 | 14,1 |
| 13 | 0,701 | 210 | 42,4 |
Табличные значения статистик: t0,95; 22 = 2,07; F0,05;2;22 = 3,44.
Вариант 9. По данным, представленным в табл. 38, изучается зависимость чистого дохода у (млрд долл.) крупнейших компаний США в 20ХХ г. от оборота капитала х1 (млрд долл.) и использованного капитала х2 (млрд долл.).
Таблица 38
| № п/п | y | x 1 | x 2 | № п/п | y | x 1 | x 2 |
| 1 | 6,6 | 6,9 | 83,6 | 11 | 4,2 | 71,9 | 32,5 |
| 2 | 3,0 | 18,0 | 6,5 | 12 | 2,7 | 93,6 | 25,4 |
| 3 | 6,5 | 107,9 | 50,4 | 13 | 1,6 | 10,0 | 6,4 |
| 4 | 3,3 | 16,7 | 15,4 | 14 | 2,4 | 31,5 | 12,5 |
| 5 | 0,1 | 79,6 | 29,6 | 15 | 3,3 | 36,7 | 14,3 |
| 6 | 3,6 | 16,2 | 13,3 | 16 | 1,8 | 13,8 | 6,5 |
| 7 | 1,5 | 5,9 | 5,9 | 17 | 2,4 | 64,8 | 22,7 |
| 8 | 5,5 | 53,1 | 27,1 | 18 | 1,6 | 30,4 | 15,8 |
| 9 | 2,4 | 18,8 | 11,2 | 19 | 1,4 | 12,1 | 9,3 |
| 10 | 3,0 | 35,3 | 16,4 | 20 | 0,9 | 31,3 | 18,9 |
Табличные значения статистик: t0,95; 17 = 2,11; F0,05;2;17 = 3,59.
Вариант 10. По данным, представленным в табл. 39, изучается зависимость чистого дохода у (млрд долл.) крупнейших компаний США в 20ХХ г. от использованного капитала х1 (млрд долл.) и численности служащих х2 (тыс. чел.).
Таблица 39
| № п/п | y | x 1 | x 2 | № п/п | y | x 1 | x 2 |
| 1 | 6,6 | 83,6 | 222,0 | 11 | 4,2 | 32,5 | 225,4 |
| 2 | 3,0 | 6,5 | 32,0 | 12 | 2,7 | 25,4 | 675,0 |
| 3 | 6,5 | 50,4 | 82,0 | 13 | 1,6 | 6,4 | 43,8 |
| 4 | 3,3 | 15,4 | 45,2 | 14 | 2,4 | 12,5 | 102,3 |
| 5 | 0,1 | 29,6 | 299,3 | 15 | 3,3 | 14,3 | 105,0 |
| 6 | 3,6 | 13,3 | 41,6 | 16 | 1,8 | 6,5 | 49,1 |
| 7 | 1,5 | 5,9 | 17,8 | 17 | 2,4 | 22,7 | 50,4 |
| 8 | 5,5 | 27,1 | 151,0 | 18 | 1,6 | 15,8 | 480,0 |
| 9 | 2,4 | 11,2 | 82,3 | 19 | 1,4 | 9,3 | 71,0 |
| 10 | 3,0 | 16,4 | 103,0 | 20 | 0,9 | 18,9 | 43,0 |
Табличные значения статистик: t0,95; 17 = 2,11; F0,05;2;17 = 3,59.
Контрольные вопросы
1. Метод наименьших квадратов для множественных моделей.
2. Интерпретация коэффициентов множественной линейной регрессии. В чем особенность и отличия от парного анализа?
3. Множественная корреляция. Что такое корреляционная матрица? Как построить корреляционную матрицу в среде EViews? Парные, частные и множественный коэффициенты корреляции.
4. Для чего необходимы частный коэффициент эластичности и стандартизированные коэффициенты регрессии?
5. В чем особенности оценки адекватности множественных моделей?
6. Гетероскедастичность множественных моделей. Как проверить остатки множественной регрессии на гетероскедастичность в среде Eviews?
7. В чем особенность использования обобщенного МНК для множественных моделей?








