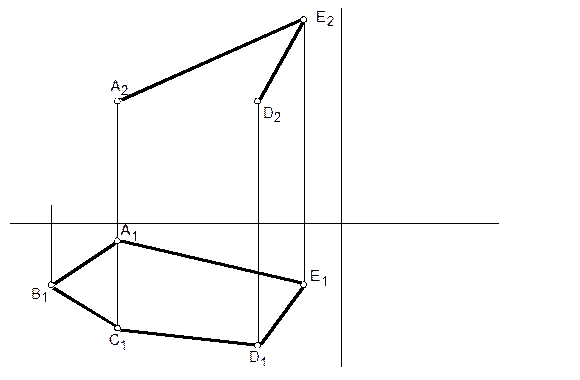Раздел 1. Основы образования чертежа .
ГТУ МОСКОВСКИЙ ИНСТИТУТ СТАЛИ И СПЛАВОВ
( МИСиС)
Кафедра Инженерной графики

Л.О.Мокрецова, В.Б.Головкина, О.Н.Чиченева, М.В.Лейкова
РАБОЧАЯ ТЕТРАДЬ
ЗАДАЧИ
к практическим занятиям по курсу
«Начертательная геометрия»
Раздаточный материал для студентов
дневной и вечерней форм обучения технических направлений
Москва, 2009
Раздел 1. Основы образования чертежа .
Подраздел 1.1. Точка. Прямая. Взаимное расположение прямых.
1. Построить три проекции треугольника по их координатам: его вершин:
А (55, 10 15), В (0, 10, 15), С (50, 0, 40) В полученном ∆АВС записать, как расположены относительно плоскостей проекций отрезки АВ, АС, ВС.
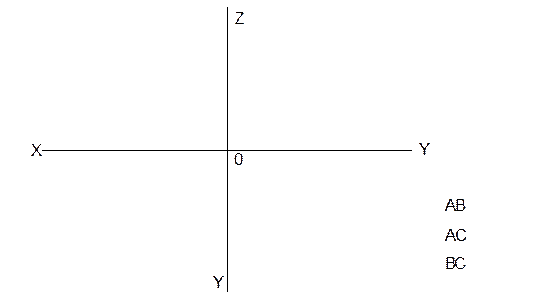
2.
а) Построить недостающие проекции точек. Записать, в каких плоскостях проекций находятся точки A, N, F. Определить видимость конкурирующих точек.
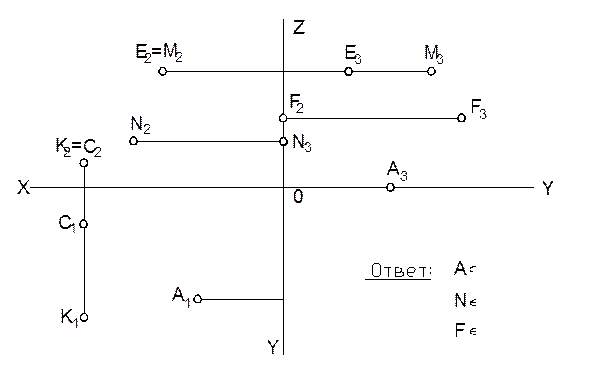
б) На безосном чертеже точка А задана тремя проекциями, остальные – двумя. Определить недостающие проекции точек. Определить видимость конкурирующих точек.
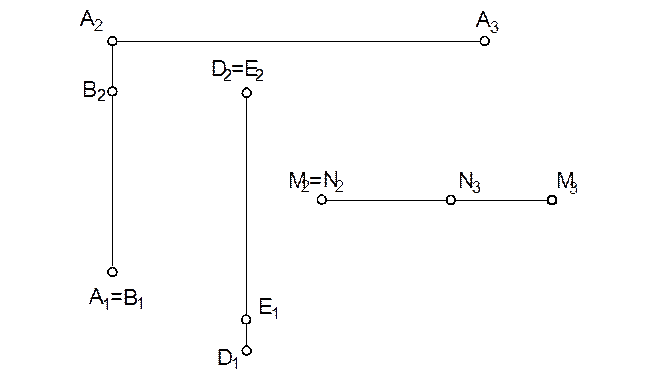
3. Построить три проекции прямых параллельных а) – фронтальной, б) – профильной плоскости проекций, проходящих через точку А. Отложить отрезки АВ = 30 мм.
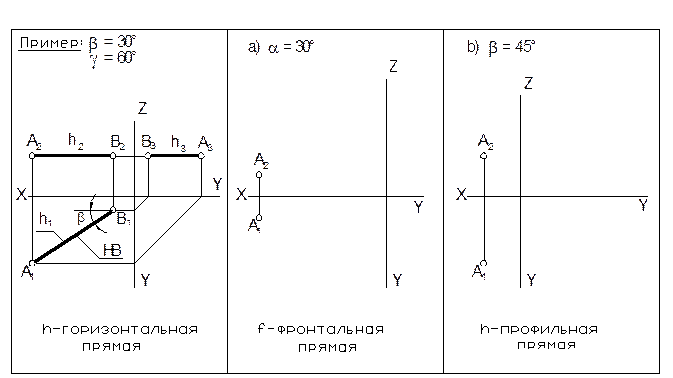
4. Через точку А провести:
1) прямую, параллельную отрезку прямой MN;
2) прямую, пересекающую отрезок MN и параллельную горизонтальной плоскости проекций.
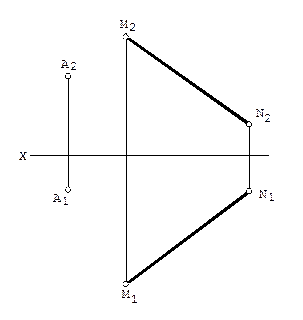
5. Через точку С провести фронтальную прямую, пересекающую отрезок АВ в точке, удаленной от П2 на 20 мм.
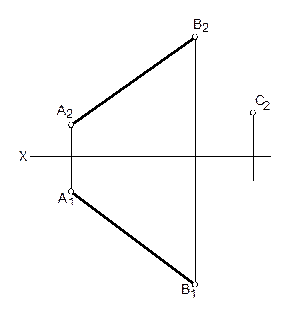
6. Построить недостающие проекции точек А и В, равноудаленных от плоскостей проекций П1 и П2.

7. Построить недостающие проекции точек А и В, если ZA = 2YA, YB = XB.
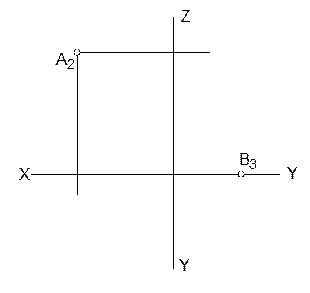
8. Определить взаимное расположение прямых. Результаты записать условными символами.
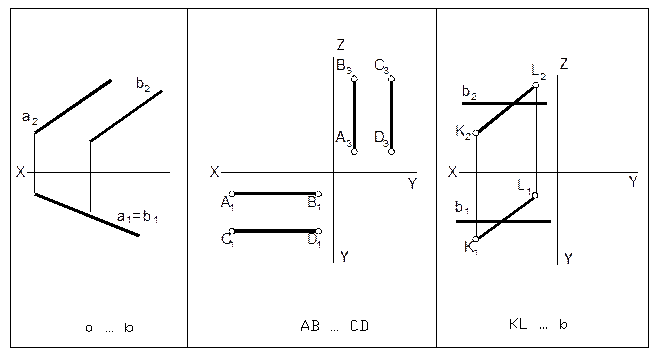
9. Провести через точку С прямую, пересекающую прямую ℓ в точке, равноудаленной от плоскостей проекций П1 и П2.
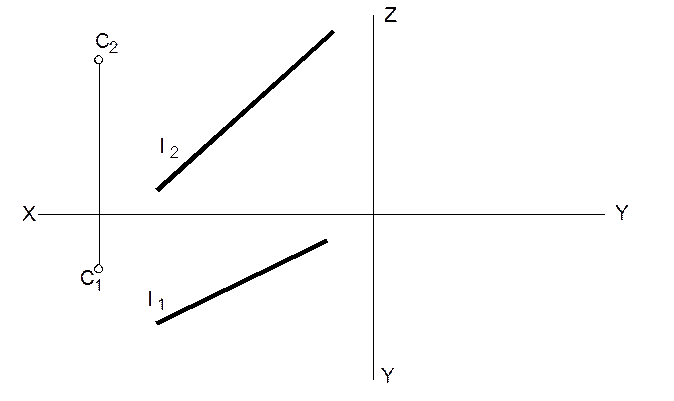
10. Как расположены прямые показанные на чертеже? На прямых с и d показать и обозначить проекции конкурирующих точек. Определить их видимость.
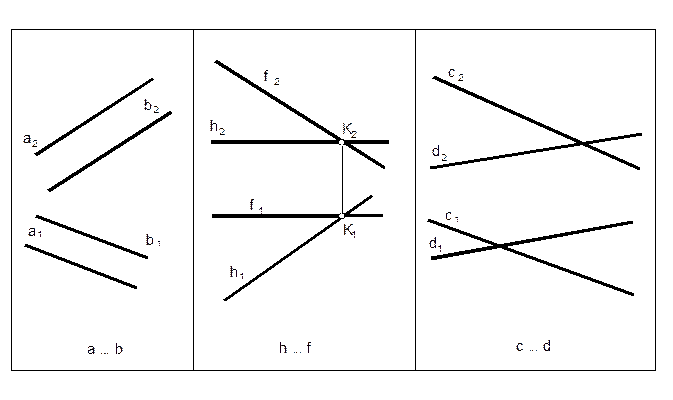
11. Через точку С провести горизонтальную прямую, пересекающую отрезок АВ в точке, удаленной от П1 на 20 мм.
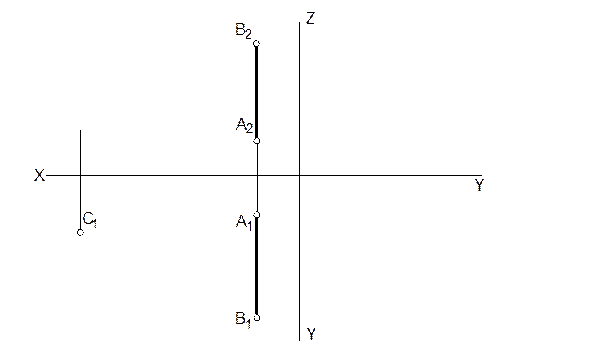
Подраздел 1.2. ПЛОСКОСТЬ. МЕТРИЧЕСКИЕ ЗАДАЧИ.
1. Определить НВ прямой АВ и угол β
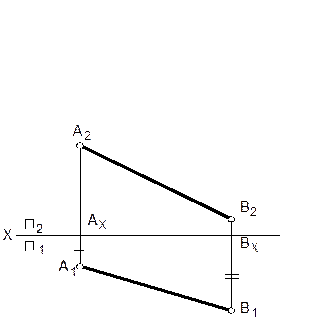
2. Построить недостающие проекции точек, лежащих в плоскости Г(a // b) и Θ (a ∩ b). Записать, как расположены Г и Θ относительно плоскостей проекций.
а)
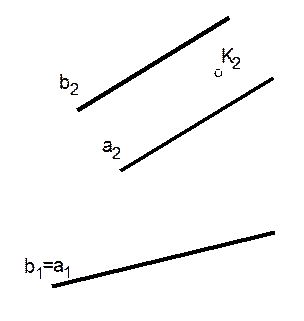
б)
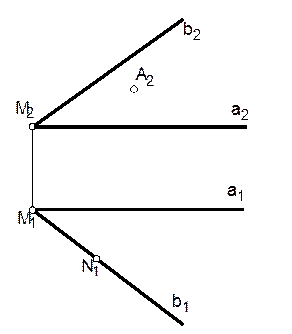
3. Построить недостающие проекции:
а) прямой а, лежащей в плоскости Г (m // n)
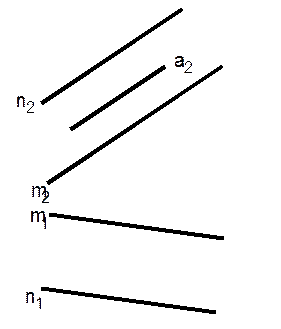
б) отрезка DK, лежащего в плоскости (AB∩AC)
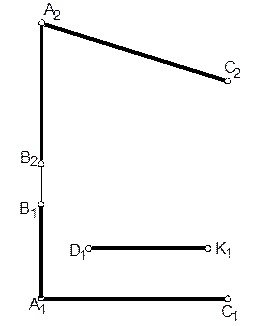
4. Через точку К провести плоскость параллельную плоскости ∆АВС. Искомую плоскость задать горизонталью и фронталью.
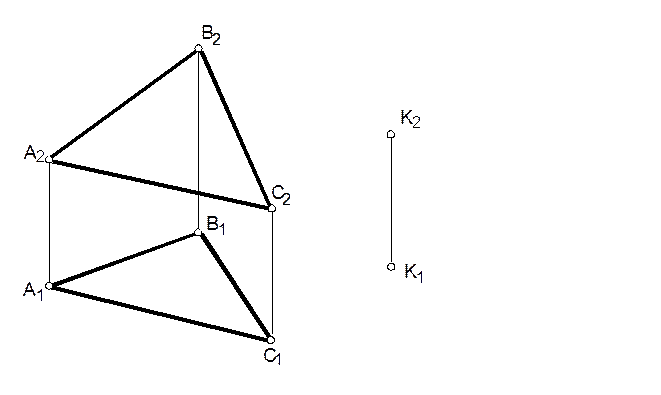
5. Определить натуральную величину угла при вершине С и построить биссектрису угла АСВ.
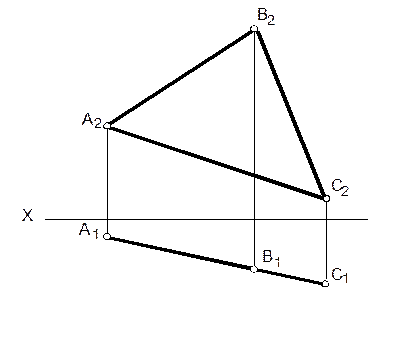
6. Построить горизонтальную проекцию треугольника АВС. Угол наклона плоскости треугольника к фронтальной плоскости равен 30°, а сторона АВ параллельна фронтальной плоскости проекций.
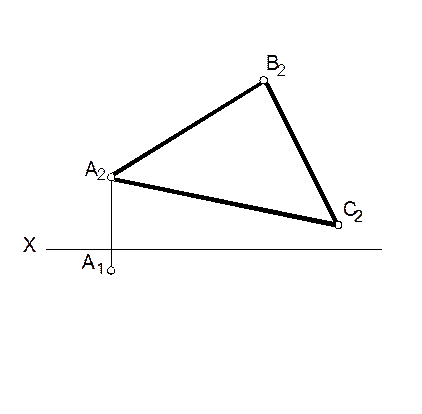
7. Определить натуральную величину плоскости ABCD и углы ее наклона к горизонтальной (Ðα) и фронтальной (Ðβ) плоскостям проекций.
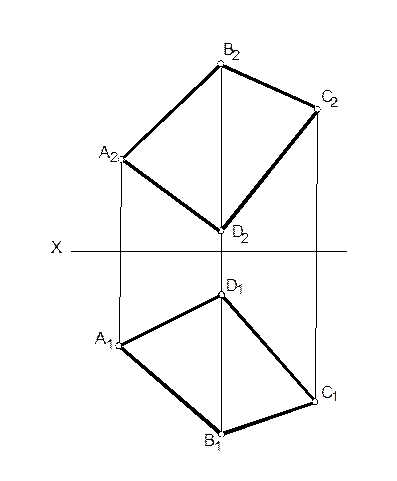
8. Построить недостающие проекции точек в системах плоскостей 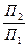 ,
, 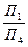 ,
, 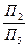
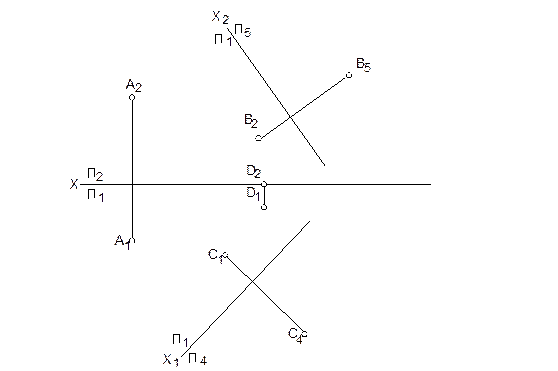
9. Определить какая из точек К или D принадлежит заданной плоскости.
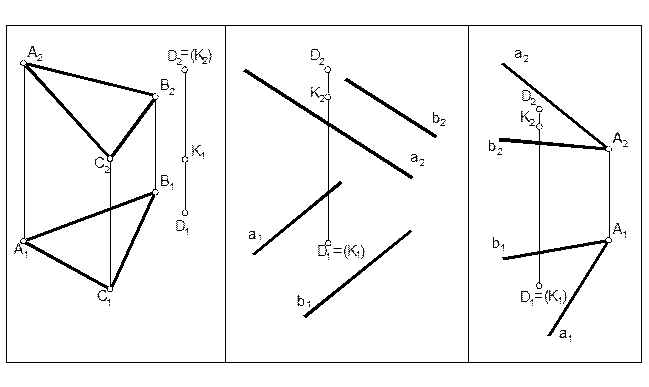
10. На отрезке АВ найти точку, отстоящую от точки А на 30 мм.
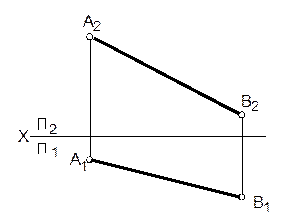
11. Построить горизонтальную проекцию отрезка DK, если угол его наклона (β) к фронтальной плоскости проекций равен 30°.
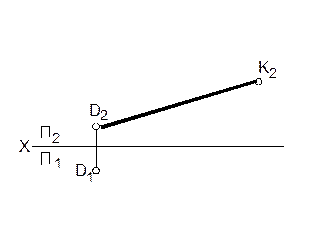
12. Построить проекции точки В, если В Î а и |АВ| = 30 мм.
а)
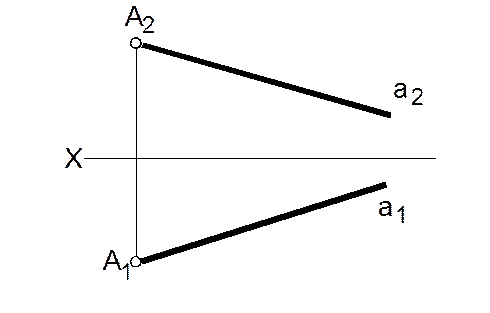
б)
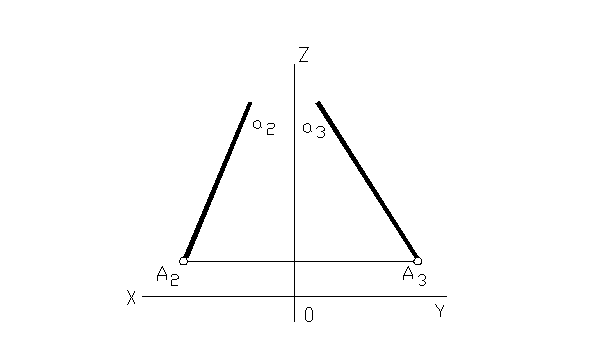
13. Достроить проекции треугольника BDE, лежащего в плоскости ∑ (ℓ×k).

14. Построить недостающие проекции плоского пятиугольника. В плоскости пятиугольника провести диагонали и определить их положение относительно плоскостей проекций.