31. Вычислить длину окружности и площадь круга одного и того же заданного радиуса R.
Линейные алгоритмы
1. Водяной паук строит в воде воздушный домик, перенося на лапках и на брюшке
пузырьки атмосферного воздуха и помещая их под купол паутины. Сколько рейсов на
до сделать пауку, чтобы построить домик объемом 1 кубический сантиметр, если
каждым раз он берет 5 кубических миллиметров воздуха?
результат: 200
2. Сложить 2 вектора, заданных своими координатами.
контрольный пример:
данные: (3,5);(6,9)
результат: (9,14)
3. Какой процент составляет число А от числа В?
контрольный пример
данные: А=5, В=10
результат: 50
4. Найти длину окружности, если известна площадь круга.
контрольный пример:
данные 6
результат: 8.681
5. Найти площадь и периметр треугольника по двум сторонам а, b и углу a между ними.
контрольный пример:
данные: а=3, b=5, a=0.5
результат: 3.5957, 10.77
6. Найти сумму арифметической прогрессии. Даны: первый член прогрессии, ее знаменатель и число членов прогрессии.
контрольный пример:
данные: a1=1,q=2,n=4
результат: 16
данные: a1=3, q=3, n=8
результат: 9840
7. Ввести первый член геометрической прогрессии а и ее знаменатель q. Вычислить
сумму ее первых 10 членов.
контрольный пример:
данные: a=3, q=2
результат: 3069
8. Каменный уголь погрузили в вагон высотой 0.76 м., длиной 6.43 м., шириной 2.74 м.
Сколько тонн угля погрузили, если удельный вес угля 1.3 т/куб.м.?
Результат: 17.407 (т.)
9. Расстояние между параллельными гранями шестигранной головки болта равно
63 мм., толщина головки равна 6.5 мм. Найти объем головки болта.
Результат: 22342,156 (кв. мм.)
10. Найти разность векторов, заданных своими координатами.
контрольный пример:
данные: (2,0), (0,2)
результат. (2,-2)
11. Написать программу нахождения р% от данного числа A.
Контрольный пример:
данные p=10, A=50
результат: 5
12. На участке длиной S1 автобус двигался со скоростью V1, на участке длиной S2 - со
скоростью V2. Найти среднюю скорость движения автобуса на всем участке длиной S=S1+S2.
контрольный пример:
данные: V1=50,V2=60,S1=10,S2=18
результат: 56
13. Найти площадь треугольника с помощью формулы Герона.
контрольный пример:
данные: 8,4,5 результат: 8.1814
14. Найти площадь кольца, если его толщина - t см, диаметр внутреннего круга - d
см.
контрольный пример:
данные: t=3, d=4
результат: 65.939
15. Вычислить длины сторон треугольника по заданным координатам его вершин.
контрольный пример:
данные: (1,4),(4,1),(4,2)
результат: 4.24,1,3.6
16. Найти сумму n первых членов геометрической прогрессии.
контрольный пример:
данные 2, 3, 5
результат: 242
17. Корова съедает в сутки около 70 кг травы, пастбищный сезон в нашей области
длится в среднем 150 суток, примерная урожайность пастбищных культур 250 ц/га.
Какова площадь культурного пастбища, необходимая для одной коровы на пастбищный
сезон ?
Результат: 0.42 (га)
18. В озеро, имеющее среднюю глубину 10 м. и площадь поверхности 20 кв. км. бросили кристалл поваренной соли массой 0.05 г. Сколько молекул этой соли оказалось
бы в наперстке воды объемом 2 куб. см,, зачерпнутой из озера, если полагать, что
соль растворилась равномерно во всем объеме воды?
Результат: 5150337.6 (мол.)
19. Зал кинотеатра вмещает 35 рядов кресел по 40 мест в ряду. Стоимость билетов: с 1 по 10 ряд - 25 копеек, 11 по 20 ряд - 40 копеек, 21 по 35 ряд - 50 копеек. Составьте алгоритм вычисления общей стоимости билетов, если зал заполнен.
результат: 560 (руб)
20. В первом сосуде содержится V1 литров воды температуры t1, во втором - V2
литров воды температуры t2, в третьем - V3 литров воды температуры t3. Воду слили в
один сосуд. Найдите объем и температуру воды а этом сосуде.
контрольный пример:
данные: v1=1, v2=2, v3=6, t1=20, t2=30, t3=100
результат: V=9, t=75.556
21. Подсчитайте сколько секунд в одном столетии. Полагая условно одну секунду одним битом информации, определите приближенно искомую величину в килобайтах.
Результат; 3153600000 (сек.), 384960,94 (Кбайт)
22. Составьте алгоритм, вычисляющий по заданным вещественным числам a, b, c, d величины ac+bd и ad-bc. Этот алгоритм может использовать промежуточные величины, операции сложения, вычитания и умножения, причем умножение должно выполняться не более трех раз.
контрольный пример:
данные: a,b,c,d=l,2,3,4
результат: 11,-2
23. На птицефермах продукцию от кур-несушек получают в течении одного года. За
год от каждой несушки получают по 253 яйца, масса яиц - 58 г. Живая масса курицы
около 1.9 кг. Во сколько раз продукция несушки превосходит ее массу.
Результат: 7.723 (раз)
24. Треугольник ABC - равносторонний, длина его стороны - а см. Треугольник DEF-
вписанный равносторонний. Найти разность площадей этих треугольников.
контрольный пример:
данные: а=9
результат: 26.305
25. Вычислить площадь треугольника, заданного координатами вершин.
контрольный пример:
данные (3,6),(2,1),(8,9)
результат: 15.499
26. Найти радиус окружности, описанной около треугольника со сторонами а,b,с.
контрольный пример:
данные: а, b,с =5, 4, 3 результат: 2.5
27. Первый член геометрической прогрессии равен 3, а ее знаменатель равен 2. Найти сумму членов этой прогрессии с 20-го по 25-й.
результат 9.9090Е+О7
28. Вычислить значения выражений по формулам № 1-12 (все переменные имеют действительный тип):
1) 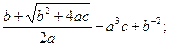 2)
2) 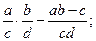
3) 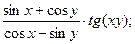 4)
4) 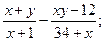

5) 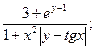 6)
6) 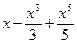 ;
;
7) 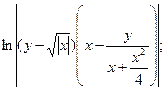 8)
8) 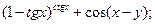
9) 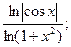 10)
10) 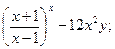
11) 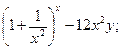 12)
12) 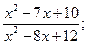
29. Вычислить периметр и площадь прямоугольного треугольника по заданным длинам двух катетов а и b.
30. Заданы координаты трех вершин треугольника (х1, у1), (х2, у2), (х3, y3). Найти его периметр и площадь.
31. Вычислить длину окружности и площадь круга одного и того же заданного радиуса R.
32. Найти произведение цифр заданного четырехзначного числа.
33. Даны два числа. Найти среднее арифметическое кубов этих чисел и среднее геометрическое модулей этих чисел.
34. Вычислить расстояние между двумя точками с данными координатами (x1, у1) и (х2, у2).
35. Даны два действительных числа х и у. Вычислить их сумму, разность, произведение и частное.
36. Дана длина ребра куба. Найти площадь грани, площадь полной поверхности и объем этого куба.
37. Дана сторона равностороннего треугольника. Найти площадь этого треугольника, его высоты, радиусы вписанной и описанной окружностей.
38. Найти площадь кольца, внутренний радиус которого равен r, а внешний — заданному числу R (R > r).
39. Треугольник задан величинами своих углов и радиусом описанной окружности. Найти стороны треугольника.
40. Найти площадь равнобедренной трапеции с основаниями а и b и углом α при большем основании а.
41. Вычислить корни квадратного уравнения ах2 + bх + с = 0, заданного коэффициентами a, b и с (предполагается, что 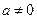 и что дискриминант уравнения неотрицателен).
и что дискриминант уравнения неотрицателен).
42. Дано действительное число х. Не пользуясь никакими другими арифметическими операциями, кроме умножения, сложения и вычитания, вычислить за минимальное число операций
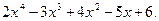
43. Дано х. Получить значения -2х+3х2 - 4х3 и 1 + 2х + Зх2 + 4х3. Позаботиться об экономии операций.
44. Найти площадь треугольника, две стороны которого равны а и b, а угол между этими сторонами равен у.
45. Дано a. Не используя никаких функций и никаких операций, кроме умножения, получить a8 за три операции; a10 и a16 за четыре операции.
46. Найти сумму членов арифметической прогрессии, если известны ее первый член, знаменатель и число членов прогрессии.
47. Найти все углы треугольника со сторонами а, b, с. Предусмотреть в программе перевод радианной меры угла в градусы, минуты и секунды.
48. Три сопротивления Rl, R2, R3 соединены параллельно. Найдите сопротивление соединения.
49. Составить программу для вычисления пути, пройденного лодкой, если ее скорость в стоячей воде v км/ч, скорость течения реки и км/ч, время движения по озеру t1 ч, а против течения реки — t2 ч.
50. Текущее показание электронных часов: t часов (0 < t < 23), m мин (0 < m < 59), k с (0 < k < 59). Какое время будут показывать часы через р ч q мин r с?
51. Полторы кошки за полтора часа съедают полторы мышки. Сколько мышек съедят X кошек за Y часов?
52. Составить программу вычисления объема цилиндра и конуса, которые имеют одинаковую высоту Н и одинаковый радиус основания R.
53. Дана величина A, выражающая объем информации в байтах. Перевести А в более крупные единицы измерения информации.
54. Составить программу, печатающую значение true, если указанное высказывание является истинным, и false в противном случае:
1) сумма двух первых цифр заданного четырехзначного числа равна сумме двух его последних цифр;
2) сумма цифр данного трехзначного числа N является четным числом;
3) квадрат заданного трехзначного числа равен кубу суммы цифр этого числа;
4) целое число N является четным двузначным числом;
5) треугольник со сторонами а, b, c является равносторонним;
6) треугольник со сторонами a, b, c является равнобедренным;
8) среди чисел а, b, с есть хотя бы одна пара взаимно противоположных чисел;
9) числа с и b выражают длины катетов одного прямоугольного треугольника, а с и d — другого. Эти треугольники являются подобными;
10) даны три стороны одного и три стороны другого треугольника. Эти треугольники равновеликие, т. е. имеют равные площади;
11) данная тройка натуральных чисел а, b, с является тройкой Пифагора, т. е. с2 = а2 + b2;
12) все цифры данного четырехзначного числа N различны;








