3.Куб описан около сферы радиуса 9,5. Найдите объем куба.

Куб описан около сферы радиуса 9. Найдите объем куба.

Куб описан около сферы радиуса 6. Найдите объем куба.

Куб описан около сферы радиуса 6,5. Найдите объем куба.

4.В цилиндрический сосуд налили 6 куб.см воды. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде увеличился в 1,8 раза. Найдите объем детали. Ответ выразите в куб.см.

4.В цилиндрический сосуд налили 4 куб.см воды. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде увеличился в 1,5 раза. Найдите объем детали. Ответ выразите в куб.см.

4.В цилиндрический сосуд налили 10 куб.см воды. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде увеличился в 1,9 раза. Найдите объем детали. Ответ выразите в куб.см.

4.В цилиндрический сосуд налили 6 куб.см воды. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде увеличился в 1,2 раза. Найдите объем детали. Ответ выразите в куб.см.

5.На расстоянии 12 см от центра шара проведено сечение, радиус которого равен 9см. Найдите объем шара и площадь его поверхности
5.Через точку, лежащую на сфере, проведено сечение радиуса 3 см под углом 600к радиусу сферы, проведенному в данную точку. Найдите площадь сферы и объем шара.
5.Все боковые ребра пирамиды равны по 2 в основании лежит равнобедренный треугольник с боковой стороной 4 и углом при основании 300.Найдите объем пирамиды.
5.Все боковые ребра пирамиды наклонены к основанию под углом 600, в основании лежит равнобедренный треугольник с боковой стороной 6 и углом при вершине 1200. Найдите объем пирамиды.
КР.Объемы тел
КР.Объемы тел
КР.Объемы тел
КР.Объемы тел
Вариант 17
Вариант 18
Вариант 19
Вариант 20
1.Найдите объем правильной шестиугольной призмы, стороны основания которой равна 12, а боковые ребра равны .
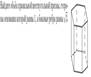
1.Найдите объем правильной шестиугольной призмы, стороны основания которой равна 9, а боковые ребра равны .
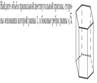
1.Найдите объем правильной шестиугольной призмы, стороны основания которой равна 1, а боковые ребра равны .
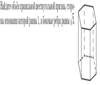
1.Найдите объем правильной шестиугольной призмы, стороны основания которой равна 7, а боковые ребра равны .
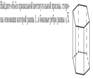
2.В правильной четырехугольной пирамиде SABCD с основанием ABCD боковое ребро SA равно 5, сторона основание равна 3. Найдите объем пирамиды.
2.В правильной четырехугольной пирамиде SABCD с основанием ABCD боковое ребро SA равно 39, сторона основание равна 15. Найдите объем пирамиды.
2.В правильной четырехугольной пирамиде SABCD с основанием ABCD боковое ребро SA равно 25, сторона основание равна 24. Найдите объем пирамиды.
2.В правильной четырехугольной пирамиде SABCD с основанием ABCD боковое ребро SA равно 30, сторона основание равна 24. Найдите объем пирамиды.
3. В основании прямой призмы лежит квадрат со стороной 4. Боковые ребра призмы равны . Найдите объем цилиндра, описанного около этой призмы.

3.Цилиндр вписан в прямоугольный параллелепипед. Радиус основания и высота цилиндра равна 13. Найдите объем параллелепипеда.

3.Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 14,5. Объем параллелепипеда равен 168,2. Найдите высоту цилиндра.

3.Куб описан около сферы радиуса 16. Найдите объем куба.
4.В сосуде, имеющем форму конуса, уровень жидкости достигает высоты. Объем жидкости равен 64 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?

4.В сосуде, имеющем форму конуса, уровень жидкости достигает высоты. Объем жидкости равен 49 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?

4.В сосуде, имеющем форму конуса, уровень жидкости достигает высоты. Объем жидкости равен 14 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?

4В сосуде, имеющем форму конуса, уровень жидкости достигает высоты. Объем жидкости равен 4 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?

5.Найдите объем пирамиды, если её основанием служит прямоугольный треугольник с гипотенузой 3 и углом 300, а боковые ребра наклонены к основанию под углом 600.
5.В конус вписана треугольная пирамида с высотой 9 и сторонами 6,8 и 10. Найдите объем конуса.
5.Около конуса описана треугольная пирамида с высотой 6 и сторонами основания 3,4 и 5. Найдите объем конуса.
5. Основание пирамиды –треугольник со сторонами 13,14 и15. Все двугранные углы при основании пирамиды равны 450. Найдите объем пирамиды.








