Полученная матрица имеет размер m ´ n и называется матрицей игры, или платежной матрицей (отсюда и название игры — матричная).
ЗАНЯТИЕ 6. МАТРИЧНЫЕ ИГРЫ
Рассмотрим игру, в которой участвуют два игрока, причем каждый из игроков имеет конечное число стратегий. Обозначим для удобства одного из игроков через A, в другого — через В. Предположим, что игрок A имеет m стратегий — А1, А2, ..., Ат, а игрок B имеет n стратегий В1, В2, ..., Вn.
Пусть игрок A выбрал стратегию Аi, а игрок B стратегию Вk. Будем считать, что выбор игроками стратегий Аi и Вk однозначно определяет исход игры — выигрыш aik игрока A и выигрыш bik игрока B, причем эти выигрыши связаны равенством
bik = - aik
(отрицательный выигрыш на бытовом языке обычно называют проигрышем).
Значения aik выигрыша при каждой паре стратегий (в каждой ситуации) {Ai, Вk}, i = 1, 2 ,..., т, k = 1, 2, ..., n (если они конечно нам известны), удобно записывать или в виде прямоугольной таблицы, строки которой соответствуют стратегиям игрока A, а столбцы — стратегиям игрока В:

или в виде матрицы

Полученная матрица имеет размер m ´ n и называется матрицей игры, или платежной матрицей (отсюда и название игры — матричная).
Рассматриваемую игру часто называют игрой m ´ n или m ´ n игрой.
Пример 1. Каждый из двух игроков A и B одновременно и независимо друг от друга записывает на листе бумаги любое целое число. Если выписанные числа имеют одинаковую четность, то игрок A получает от игрока B 1 рубль, а если разную, то наоборот — игрок A платит 1 рубль игроку В.
У игрока A две стратегии: A1 — записать четное число и A2 — записать нечетное число. У игрока B такие же две стратегии: B1 — записать четное число и B2 — записать нечетное число. Выбор игроками соответственно стратегий Ai и Bk однозначно определяет исход игры — выигрыш игрока A.
Матрица этой 2 × 2 игры имеет следующий вид
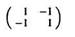
(здесь строки соответствуют стратегиям игрока A, а столбцы — стратегиям игрока В).
Пример 2. Два игрока A и B, не глядя друг на друга, кладут на стол по картонному кружку красного (r), зеленого (g) или синего (b) цветов, сравнивают цвета кружков и расплачиваются друг с другом так, как показано в матрице игры
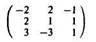
(напомним, что у этой 3 × 3-матрицы строки соответствуют стратегиям игрока A, а столбцы — стратегиям игрока B).
Считая, что эта 3 × 3 игра повторяется многократно, попробуем определить оптимальные стратегии каждого из игроков.
Начнем с последовательного анализа стратегий игрока A, не забывая о том, что, выбирая стратегию игрока A, должно принимать в расчет, что его противник B может ответить на нее той из своих стратегий, при которой выигрыш игрока A будет минимальным.
Так, на стратегию A1 он ответит стратегией В1 (минимальный выигрыш равен -2, что на самом деле означает проигрыш игрока A, равный 2), на стратегию A2 — стратегией B2 или В3 (минимальный выигрыш игрока A равен 1), а на стратегию А3 — стратегией B2 (минимальный выигрыш игрока А равен -3).
Запишем эти минимальные выигрыши в правом столбце таблицы:

Maxmin. Неудивительно, что игрок A останавливает свой выбор на стратегии A2, при которой его минимальный выигрыш максимален (из трех чисел -2, 1 и -3 максимальным является 1):

Если игрок A будет придерживаться этой стратегии, то ему гарантирован выигрыш, не меньший 1, при любом поведении противника в игре.
Аналогичные рассуждения можно провести и за игрока B. Так как игрок B заинтересован в том, чтобы обратить выигрыш игрока A в минимум, то ему нужно проанализировать каждую свою стратегию с точки зрения максимального выигрыша игрока A.
Выбирая свою стратегию, игрок B должен учитывать, что при этом стратегией его противника A может оказаться та, при которой выигрыш игрока A будет максимальным. Так, на стратегию В1 он ответит стратегией А3 (максимальный выигрыш игрока A равен 3), на стратегию B2 — стратегией А1 (максимальный выигрыш игрока A равен 2), а на стратегию В3 — стратегией A2 или А3 (максимальный выигрыш игрока A равен 1). Эти максимальные выигрыши записаны в нижней строке таблицы

Minmax. Неудивительно, если игрок B остановит свой выбор на стратегии В3, при которой максимальный выигрыш игрока A минимален (из трех чисел 3, 2 и 1 минимальным является 1):

Если игрок B будет придерживаться этой стратегии, то при любом поведении противника он проиграет не больше 1.
В рассматриваемой игре числа maxmin и minmax совпали maxmin = minmax = 1

Выделенные стратегии A2 и В3 являются оптимальными стратегиями игроков A и B,
A2 = Aopt, B3 = Bopt,
в следующем смысле:
при многократном повторении игры отказ от выбранной стратегии любым из игроков уменьшает его шансы на выигрыш (увеличивает шансы на проигрыш).
Пример 3. Рассмотрим 3 × 3 игру, заданную матрицей

Применив предложенный алгоритм находим нижнюю цену игры a = -2 и соответствующую ей стратегию A2, и верхнюю цену игры β = 2 и соответствующую ей стратегию В2.
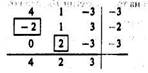
Нетрудно убедиться в том, что пока игроки придерживаются этих стратегий, средний выигрыш при многократном повторении игры равен 1. Он больше нижней цены игры, но меньше верхней цены.
Однако если игроку B станет известно, что игрок A придерживается стратегии А2, он немедленно ответит стратегией В1 и сведет его выигрыш к проигрышу -2. В свою очередь, на стратегию В1 у игрока А имеется ответная стратегия А1, дающая ему выигрыш 4. Тем самым, ситуация {A2, B2} равновесной не является.








