Рассмотрим равновесие твердое тело ⇄ жидкость на примере плавления льда (рис. 2, б)
Н2О(т) ⇄ Н2О(ж).
Функцию внешней среды выполняют нагреватель или холодильник, обменивающиеся с системой лед – жидкая вода энергией в форме теплоты.
При плавлении льда энергия нагревателя расходуется на разрушение кристаллической решетки (Q = DНпл.). Из однофазной системы (рис. 2, а) возникает равновесная двухфазная система (рис. 2, б). До завершения плавления последнего кристалла льда температура остается постоянной (Тпл. = const), если сохраняется постоянное давление. Только после превращения двухфазной системы в однофазную (рис. 2, в) температура будет повышаться в результате нагревания жидкой воды.
Рис. 2. Расчет числа степеней свободы при равновесном фазовом переходе лед⇄ вода (плавление льда и его кристаллизация)
Обратимся к равновесной системе жидкость ⇄ пар, представленной на рис. 3, б.
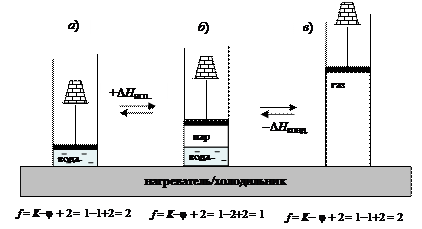
Рис. 3. Расчет числа степеней свободы при равновесном фазовом переходе вода ⇄ пар (испарение воды и конденсация пара)
Фазовые равновесия:
твердое тело ⇄ жидкость,
жидкость ⇄ пар,
твердое тело ⇄ пар
описываются уравнением Клаузиуса – Клапейрона:
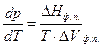, (1.1)
где DНф.п. – энтальпия фазового перехода 1 моль вещества из фазы (II) в фазу (I); DVф.п. = V(I) – V(II) – изменение объема 1 моль вещества при фазовом переходе; Т – температура фазового перехода (температура плавления, кипения или возгонки).
Отступление. Зависимость давления от температуры для фазовых равновесий в однокомпонентных системах:
твердое тело ⇄ жидкость,
жидкость ⇄ пар,
твердое тело ⇄ пар,
можно вывести, рассматривая термодинамическое равновесие фаз (I) и (II).
Условию равновесия отвечает равенство: △G = 0 или G(I) = G(II) при постоянстве давления р и температуры Т. Изменение давления и температуры от р до р + dp и от Т до Т + dT приведет к изменению функции Гиббса:
dG(I) = dG(II). (1.2)
Вспоминаем, что G = U + pV - TS и
dG = dU + pdV + Vdp - TdS – SdT.
Из первого закона термодинамики следует dU + pdV - TdS = 0, следовательно,
dG = Vdp – SdT . (1.3)
Из уравнений (1.2) и (1.3) получаем:
V(I)dp – S(I)dT = V(II)dp – S(II)dT,
[V(I) – V(II)]dp = [S(I) – S(II)] dT,
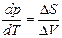или 
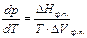
уравнение Клаузиуса – Клапейрона
Применим уравнение Клаузиуса – Клапейрона к фазовому равновесию твердое тело – жидкость.
Пример. Удельный объем льда при 0 оС (273.15 К) равен 1.091 см3/г; удельный объем жидкой воды при той же температуре равен 1.000 см3/г. Удельная энтальпия плавления льда равна DНпл.= 317.8 Дж/г. Вычислим изменение температуры плавления льда DТ при увеличении внешнего давления от 1 до 2 атм. (1 атм = 1.013×105 Па).
Решение. В соответствии с уравнением Клаузиуса – Клапейрона
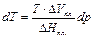
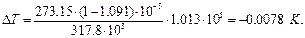
При увеличении внешнего давления на 1 атм температура плавления льда уменьшится на 0.0079 градуса.
Решение уравнения Клаузиуса – Клапейрона для фазовых переходов жидкость ⇄ пар и твердое тело ⇄ пар опирается на положение о том, что объем конденсированной фазы пренебрежимо мал по сравнению с объемом газовой фазы:
DVф.п. = V пар – Vжидк. » Vпар и
DVф.п. = Vпар – Vтв. » Vпар.
В этом легко убедиться, сравнивая, например, объем 1 моль жидкой воды (18 см3) и пара (22 400 см3) при нормальных условиях.
Принимая во внимание, что △Vф.п. @ Vпар, запишем уравнение (1.1):
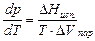. (1.4)
Будем считать, что газообразная фаза при невысоких давлениях ведет себя как идеальный газ: pV = nRT или
V = RT/p, если n =1 (1.5)
Комбинация уравнений (1.4) и (1.5) позволяет установить зависимость равновесного давления пара над жидкостью (или твердым телом) от температуры:
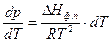
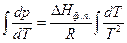+ lnA
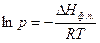+ lnA, отсюда
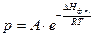, (1.6)
где р – равновесное давление пара над жидким или твердым индивидуальным соединением; А – постоянный множитель, зависящий от природы соединения; Т – температура, отвечающая состоянию равновесия; D Hф.п. – энтальпия фазового перехода (DHисп. или DHвозг.).
Отступление. Одним из примеров преобразования энергии фазовых переходов в механическую работу служит паровая турбина. В качестве энергоносителя (рабочего тела) используется вода. Водяной пар получают в процессе испарения воды в паровом котле высокого давления. Давление пара над жидкостью при повышении температуры в закрытом паровом котле достигает десятков и сотен атмосфер. При высоких давлениях свойства водяного пара отличаются от свойств идеального газа. В этом легко убедиться, сравнивая экспериментальные значения давления водяного пара (рис. 4) и давления пара, вычисленные по уравнению (1.6)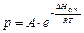 
, где р [Па]; А = 14.8×1010; △Нисп. = 44010 [кДж/моль]; R = 8.314 [Дж/(моль×К)]; Т [К]. В паровых котлах применяется, как правило, так называемый «перегретый пар» – газообразное состояние воды в отсутствии жидкой фазы. В паровую турбину поступает перегретый пар при температуре 550 оС и давлении 255 атм. На рис. 5. представлена область равновесия жидкая вода – пар, для которой характерно экспоненциальное нарастание давления с ростом температуры. После превращения всей воды в пар увеличение давления с ростом температуры носит линейный характер. Перегретый пар при высоких давлениях не подчиняется уравнению состояния идеального газа (р V = nRT), но тенденция линейной зависимости давления от температуры приближенно сохраняется.
Рис. 4. Равновесная система вода ⇄ пар. Зависимость давления пара от температуры при V = const и расчет числа степеней свободы в системе.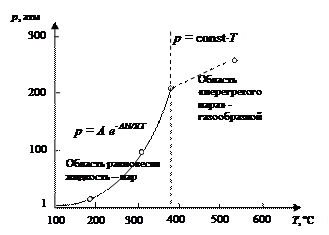 
Рис. 5. Зависимость давления от температуры в системе вода – пар
Кинетическая энергия молекул пара в паровом котле преобразуется в механическую энергию вращения вала паровой турбины. Струя пара «бьет» по лопаткам вала и вращает турбину со скоростью 3000 об/мин. Вал турбины непосредственно соединен с электрогенератором, в котором механическая энергия вращения вала преобразуется в электрическую. В современных паровых турбинах используют перегретый пар и при более высоких температурах и давлениях, например, при 650 оС, р = 350 атм. Принципиальная схема установки, преобразующей тепловую энергию в электрическую энергию, представлена на рис. 6.
 |
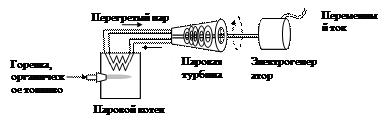Рис. 6. Модель, демонстрирующая превращение энергии фазового перехода жидкость – пар в механическую энергию движения и затем в электрическую
При температуре ниже 0 оС и давлении ниже 0.006 атм существует равновесие лед⇄пар: Н2О(т) ⇄ Н2О(пар)
Отступление. Давление насыщенного пара воды надо льдом не превышает нескольких миллиметров ртутного столба (рис. 7).
 |
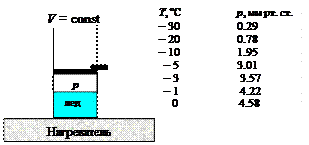Рис. 7. Равновесная система лед ⇄ пар (V = const)
Но этого количества пара достаточно, чтобы покрыть инеем ветви деревьев и провода высоковольтной линии электроснабжения в зимнее время года при резком понижении температуры воздуха.
На рис. 8 в координатах р – Т приведена фазовая диаграмма воды.
 |
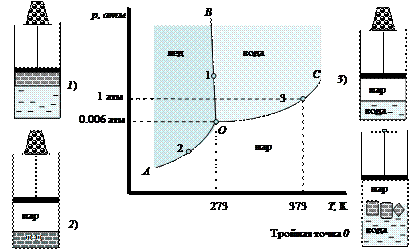Рис. 8. Фазовая диаграмма состояния воды
Фазовая диаграмма представляет графическую форму фазового равновесия твердое тело – жидкость – пар. На диаграмме выделяются три области: лед, вода, пар. Каждой области соответствует одна фаза (j = 1). Применив правило фаз, получаем число степеней свободы для однофазных систем:
f = К – j +2 = 1 – 1 + 2 = 2
Любая точка однофазной системы обладает двумя степенями свободы. Можно без изменения числа фаз произвольно изменять р и Т в пределах, ограниченных кривыми АОВ для льда, ВОС для воды или АОС для пара.
Кривые ОВ, ОС и ОА соответствуют двухфазным системам лед ⇄ вода, вода ⇄ пар и лед ⇄ пар.
Согласно правилу фаз:
f = K -j + 2 = 1 – 2 + 2 = 1
Однокомпонентные двухфазные системы имеют одну степень свободы. Например, можно менять произвольно температуру, но при этом для сохранения числа фаз давление должно определяться ходом кривых ОА, ОВ или ОС. Можно менять произвольно давление, тогда температура будет определяться ходом все тех же кривых ОА, ОВ или ОС.
Точка О отвечает трехфазной системе (лед – жидкость – пар). Это единственное состояние, для которого число степеней свободы равно нулю f = K -j + 2 = 1-3+2 = 0. Система инвариантна.
1.2. Двухкомпонентные системы
В двухкомпонентной системе (К=2), в которую входят соединения А и В, число переменных равно четырем: р, Т, сА, сВ. При постоянном давлении (р = const) состояние двухкомпонентной системы можно рассматривать на плоской диаграмме температура – состав и правило фаз принимает вид:
f = K - j +1 или f = 3 - j .
Рассмотрим случай двухкомпонентной системы, в которой компоненты неограниченно растворимы в расплаве и практически нерастворимы в твердой фазе. Такой тип фазовой диаграммы, называемой диаграммой плавкости, представляет система Cd – Bi (рис. 9).
Диаграмма плавкости строится по кривым охлаждения. Чтобы получить кривые охлаждения, готовят расплавы различного состава. Затем наблюдают процесс охлаждения и кристаллизации расплавов во времени. Кривые 1 и 6 отвечают охлаждению и кристаллизации расплава чистых Cd (кривая 1) и Bi (кривая 6). При кристаллизации расплавов индивидуальных Cd и Bi наблюдаются четко выраженные температурные остановки (горизонтальные участки). Температура не изменяется до тех пор, пока не закристаллизуется последняя капля расплава индивидуального вещества.
 |
Рис. 9. Диаграмма плавкости двухкомпонентной системы Cd – Bi (правая часть), построенная по кривым охлаждения расплава Cd – Bi (левая часть рисунка)
При охлаждении двухкомпонентного расплава процесс кристаллизации начинается с выпадения кристаллов одного из компонентов. Так из расплава, содержащего 70% Сd и 30% Bi (кривая охлаждения 2, точка а), происходит выпадение кристаллов Cd. Процесс кристаллизации Cd изменяет состав расплава, он обогащается Bi, поэтому температура кристаллизации плавно уменьшается по мере выпадения кристаллов Cd. Так происходит до температуры, соответствующей точке б на кривой 2. Температура расплава, соответствующая точке б, остается некоторое время постоянной. Из расплава одновременно выпадают кристаллы Cd и Bi в том соотношении, которое соответствует составу расплава. Температура расплава остается постоянной до тех пор, пока не завершится выпадение смеси кристаллов Cd и Bi постоянного состава (плато б – с на кривой 2). Эта температурная остановка (плато б – с на кривой 2) соответствует точке 4 на диаграмме плавкости. Данная точка называется эвтектической. Расплав, находящийся в равновесии с кристаллами обоих компонентов, называется эвтектической смесью или эвтектикой, а температура кристаллизации жидкой эвтектики – эвтектической точкой.
Кривая охлаждения 3 повторяют процесс, описанный для кривой 2, с той лишь разницей, что исходный состав расплава 60% Cd + 40% Bi и начало кристаллизации Сd отвечает точке 3 на диаграмме плавкости. Аналогично возникает точка 5 на диаграмме состояния при охлаждении жидкого расплава 20% Cd + 80% Bi, а при кристаллизации происходит выпадение кристаллов Bi (кривая охлаждения 5). Кривой охлаждения 4 соответствует кристаллизация эвтектической смеси.
В расплаве число степеней свободы f = K – j + 1 =2 – 1+1 = 2, т.е.система остается однофазной при произвольном изменении Т и состава.
На линиях 1 – 4 и 4 – 6 (рис. 9, правая часть), отвечающих равновесию бинарного расплава и кристаллов Cd или Bi, число степеней свободы равно: f = K – j + 1 =2 – 2+1 = 1. Это значит, что для сохранения двух фаз можно менять либо Т, либо состав. В эвтектической точке 4 в равновесии находятся 3 фазы: расплав, кристаллы Bi и кристаллы Cd. Система инвариантна, так как f = K – j + 1 =2 – 3+1 =0
Многие водные растворы солей представляют собой подобные двухкомпонентные системы. На рис. 10 показана диаграмма состояния двухкомпонентной системы Н2О -NaCl. Выше линий bc и сdf существует раствор NaCl в воде. Область, охваченная кривыми abc, представляет собой гетерогенную смесь раствора соли с плавающими в нем кристаллами льда. Область, охваченная кривыми cdf, – гетерогенная смесь кристаллов NaCl в растворе. Поле ниже линии acg – кристаллы льда и соли.
 |
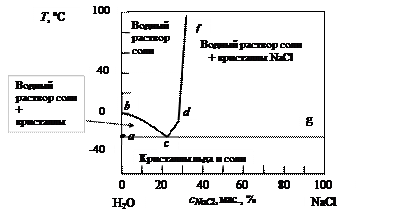Рис. 10. Диаграмма состояния двухкомпонентной системы Н2О -NaCl:
Краткий итог темы
1. Каждая фаза является гомогенной (однородной) системой. Если существует несколько фаз, находящихся в термодинамическом равновесии, система становится гетерогенной (неоднородной). Внешним признаком гетерогенной системы является наличие поверхности раздела фаз. Под фазой подразумевается гомогенная часть равновесной гетерогенной системы, характеризующаяся одинаковыми физическими и химическими свойствами во всех ее частях.
2. В зависимости от числа фаз (j), которые находятся в термодинамическом равновесии, и числа компонентов (К) гетерогенной системы, число степеней свободы (f), т.е. число переменных, которое можно изменять, не изменяя число фаз, вычисляется в соответствии с правилом фаз Гиббса по уравнению:
f = К - j + 2,
если переменными являются давление р и температура Т,
или по уравнению:
f = К - j + 1
если переменными являются р, с1, с2 или Т, с1, с2.
3. Для любой однокомпонентной системы (К=1) максимальное число фаз – три: твердая, жидкая и газообразная. В этих системах фазы обладают одинаковыми химическими свойствами, но различаются физическими свойствами.
4. Фазовая диаграмма позволяет представить в графической форме фазовые равновесия для однокомпонентных систем: твердое тело ⇄ жидкость, жидкость ⇄ пар, твердое тело ⇄ пар, как функцию температуры и давления. Она базируется на приложении правила фаз.
5. Зависимость давления пара от температуры описывается уравнением Клаузиуса – Клапейрона.
р = А е- D Н/ RT ,
где р – равновесное давление пара над жидким или твердым индивидуальным соединением; А – постоянный множитель, зависящий от природы соединения; Т – температура, отвечающая состоянию равновесия; D H – энтальпия фазового перехода (DHисп. или DHвозг.).
Термины для запоминания
Компонент – вещество, входящее в состав системы, которое может быть выделено и способно существовать вне ее в качестве индивидуального соединения.
Фаза – гомогенная часть равновесной гетерогенной системы, характеризующаяся одинаковыми физическими и химическими свойствами во всех ее частях.
Фазовая диаграмма для однокомпонентной системы представляет графическую форму фазового равновесия твердое тело – жидкость – пар.
Фазовые равновесия – сосуществование термодинамически равновесных фаз, образующих гетерогенную систему.
Число степеней свободы ( f ) указывает количество переменных, изменение которых не приведет к изменению числа фаз системы.
Эвтектической смесью или жидкой эвтектикой называются расплавы, находящиеся в равновесии с кристаллами обоих компонентов, а температура ее кристаллизации - эвтектической точкой.