Общее условие химического равновесия
В случае смеси веществ, а таковой является, например, смесь исходных веществ и продуктов химической реакции
nАА + nВВ ⇄ nСС + nDD,
функция Гиббса будет зависеть не только от давления и температуры, но и от количества веществ nA, nВ, nС, nD участников реакции
G = f(p, T, nA, nВ, nС, nD). (4.46)
Полный дифференциал функции Гиббса
|
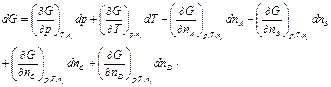
Знак (-) в уравнении (4.47) означает, что количество nA и nВ моль исходных веществ в процессе достижения химического равновесия уменьшается, а продуктов реакции nС и nD увеличивается.
При постоянном составе системы, согласно уравнениям (4.43) и (4.44), частные производные равны энтропии и объему системы в целом
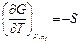 ,
,
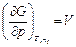 ,
,
а частные производные функции Гиббса
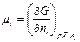
есть химические потенциалы компонентов смеси (символ i обозначает компоненты А, В, С и D, а символ j обозначает компоненты, концентрация которых не меняется при изменении концентрации компонента i).
Выражение (4.47) можно представить в виде:
dG = Vdp - SdT - mAdnA - mBdnB + mCdnC + mDdnD.
Если химическое равновесие устанавливается при постоянной температуре и давлении (р,Т = const), то
dG = - mAdnA - mBdnB + mCdnC + mDdnD. (4.48)
Условимся считать, что химические потенциалы m i не зависят от количества моль компонентов смеси. Тогда интегрирование функции Гиббса от G 1 до G 2 , а количества моль реагентов и продуктов реакции от 0 до n i дает:
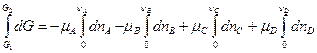 ,
,
DG = - nАmA - nВmB + nСmC + nDmD,
DG = Snimi. (4.49)
При достижении равновесия DG = 0, и уравнение (4.49) примет вид:
Snimi = 0. (4.50)
Уравнение (4.50) в общей форме выражает условие химического равновесия. Зная, что m i = m i 0 + RT lnpi ,, получаем
Snimi = - nАm0A- nАRT lnpA - nВm0B - nВ RT lnpB
+ nСm0C + nСRT lnpC + nDm0D + nDRT lnpD = 0
или
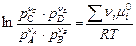 . (4.51)
. (4.51)
В правую часть уравнения (4.51) входят постоянные параметры, если принять во внимание, что процесс проводят при постоянной температуре (Т = const). Тогда из уравнения (4.51) следует
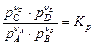 . (4.52)
. (4.52)
Кр – константа равновесия химической реакции, pA , pB , pC , pD – парциальные давления компонентов смеси.
Уравнение (4.52) является одной из форм выражения закона действующих масс.
В случае неравновесного состояния системы следует пользоваться уравнением (4.49). Если подставить в уравнение DG = Snimi химические потенциалы участников реакции, то получим уравнение изотермы реакции Вант-Гоффа:
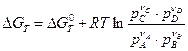 . (4.53)
. (4.53)
В уравнении изотермы реакции (4.53) даны произвольные неравновесные парциальные давления участников реакции. В случае равенства всех неравновесных давлений единице (стандартное условие) уравнение изотермы приобретает вид:
- 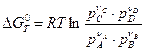 или
или 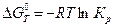 . (4.54)
. (4.54)
Рассмотрим выражения константы равновесия гомогенной и гетерогенной реакций. Для гомогенной реакции образования аммиака, протекающей в газовой фазе,
N2(г) + 3H2(г) ⇄ 2NH3(г)
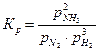 .
.
В случае гетерогенной реакции, наряду с газообразными веществами, участвуют конденсированные фазы, каждая из которых состоит только из одного компонента (чистого вещества). Например,
СаСО3(т) ⇄ СаО(т) + СО2(г)
в газовой фазе отсутствуют пары твердых веществ СаСО3 и СаО. Тогда, согласно уравнению (4.50), условие химического равновесия запишется следующим образом:
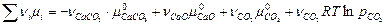 = 0
= 0
или
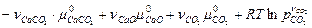 = 0,
= 0,
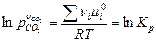 или
или
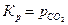
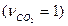 .
.
Аналогично для равновесной реакции
С(т) + СО2(г) ⇄ 2СО(г),
выражение константы химического равновесия примет вид:
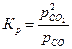 .
.
Таким образом, в случае гетерогенной реакции в выражение константы равновесия входят парциальные давления только газообразных участников реакции.








