Приближенное вычисление функции Гиббса.
Третий закон термодинамики
В зависимости от требуемой точности вычисление изменения функции Гиббса (в дальнейшем будем это изменение называть просто функцией Гиббса) по уравнению 4.35 может быть сделано в трех классических приближениях. Мы ограничимся приближенным расчетом. Будем считать, что 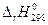 и
и 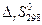 не зависят от температуры, т.е. сохраняют свои значения, определенные при 298 К, и при других значениях температуры Т, тогда
не зависят от температуры, т.е. сохраняют свои значения, определенные при 298 К, и при других значениях температуры Т, тогда
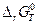 =
= 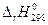 – Т ×
– Т × 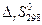 . (4.36)
. (4.36)
Для вычисления 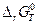 используют термодинамические данные (табл. 4).
используют термодинамические данные (табл. 4).
Обратим внимание на абсолютные значения энтропии химических соединений 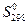 , приведенные в табл. 4.
, приведенные в табл. 4.
Согласно уравнению второго закона термодинамики
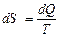 или
или 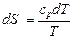 . (4.37)
. (4.37)
Интегрируем уравнение (4.37) в пределах от 0 до Т
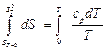 ,
,
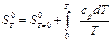 . (4.38)
. (4.38)
Т а б л и ц а 4
Стандартные энтальпии образования и абсолютные энтропии
некоторых веществ
| Вещество | 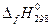 , кДж/моль , кДж/моль
| 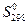 ,Дж/моль К ,Дж/моль К
|
| С(графит) | 0 | 5.74 |
| С(алмаз) | 1.897 | 2.38 |
| СО2(г.) | - 393.51 | 213.6 |
| СаСО3(кальцит) | - 1206 | 92.9 |
| СаО(кр.) | - 635.1 | 39.7 |
| Са(ОН)2(кр) | - 986.2 | 83.4 |
| Н2О(г.) | - 241.84 | 188.74 |
| Н2О(ж.) | - 285.84 | 69.96 |
| Н2О(кр.) | - 291.84 | 39.33 |
Согласно статистической термодинамике, энтропия является мерой беспорядка. М. Планк предложил постулат: энтропия правильно сформированного твердого тела при абсолютном нуле равна нулю.
Это формулировка третьего закона термодинамики. При температуре Т =0 К все вещества находятся в твердом состоянии, а кристалл с идеальной упорядоченностью должен иметь 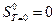 .
.
В соответствии с третьим законом термодинамики абсолютная энтропия индивидуального вещества при температуре Т К определяется по формуле:
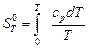 . (4.39)
. (4.39)
На пути перехода кристаллического вещества от 0 до Т встречаются фазовые переходы кристалл – жидкость и жидкость – газ. Энтропия фазовых переходов учитывается при вычислении абсолютного значения энтропий.
Пример. Для получения негашеной извести используют минерал СаСО3. Определим температуру разложения карбоната кальция. Считаем, что процесс идет про постоянном давлении р = 1 атм (давление углекислого газа).
СаСО3(т) ® СаО(т) + СО2(г); 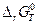 = ?
= ?
Для расчета температуры разложения СаСО3 воспользуемся функцией Гиббса Dr G0 = Dr Н0 – ТDr S0 и рассчитаем
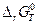 =
= 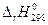 – Т ×
– Т × 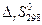 ,
,
делая допущение, что DrН0 и Dr S0 не зависят от температуры. Величины 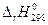 и
и 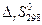 для вышеуказанной реакции найдем, используя закон Гесса и данные табл. 4.
для вышеуказанной реакции найдем, используя закон Гесса и данные табл. 4.
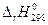 = – 635,1 – 393,51 – [–1206] = 177,4 кДж.
= – 635,1 – 393,51 – [–1206] = 177,4 кДж.
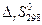 = 39,7 + 213,6 – 92,9 =160,4 Дж = 0,1604 кДж/моль.
= 39,7 + 213,6 – 92,9 =160,4 Дж = 0,1604 кДж/моль.
Находим температуру разложения СаСО3, при которой достигается термодинамическое равновесие, т. е. 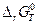 = 0.
= 0.
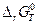 = 177.4 – Т×0,1604 =0,
= 177.4 – Т×0,1604 =0,
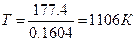 или » 833 0С.
или » 833 0С.
Выше 833 0С реакция разложения карбоната кальция с образованием углекислого газа и оксида кальция (негашеной извести) термодинамически разрешена.
4.6. Термодинамический взгляд на химическое равновесие. Химический потенциал индивидуального соединения
Рассмотрим обратимую химическую реакцию
nАА + nВВ ⇄ nСС + nDD,
где ni – стехиометрические коэффициенты.
Общее условие химического равновесия можно получить, используя химические потенциалы mА, mВ, mС, mD участников процесса.
Выведем уравнение, выражающее химический потенциал индивидуального соединения. В основном химические процессы проводят в условиях, определяемых внешним давлением и температурой. В этом случае критерием направления процесса является функция Гиббса.
G = f(p , T)
или G = U + pV – TS .
Полный дифференциал функции Гиббса
dG = dU + pdV +Vdp – TdS – SdT. (4.40)
Согласно первому и второму законам термодинамики d Q= dU + pdV и d Q = TdS . Отсюда следует обобщенное уравнение:
dU + pdV = TdS или dU + pdV – TdS = 0. (4.41)
Подставляя уравнение (4.41) в (4.40), получаем:
dG = Vdp – SdT. (4.42)
При р = const уравнение (4.42) преобразуется в
dG = – SdT или 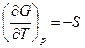 , (4.43)
, (4.43)
а при Т = const
dG = Vdp или 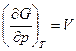 . (4.44)
. (4.44)
Для одного моль (n = 1) чистого газообразного вещества, проявляющего свойства идеального газа,
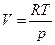 . (4.45)
. (4.45)
Комбинируя уравнения (4.44) и (4.45), получим при T = const
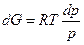 .
.
Интегрирование последнего уравнения в пределах от р = 1 атм до р приводит к уравнению, выражающему зависимость химического потенциала от температуры и давления.
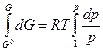
G = G0 + RT lnp или
m = m0 + RT lnp .
Функция Гиббса, рассчитанная на моль индивидуального вещества, есть мольный химический потенциал индивидуального вещества.








