Работа А – это форма обмена энергией системы с окружающей средой посредством направленного движения макросистемы как целого.
Например, газ в цилиндре под поршнем расширяется и совершает работу, поднимает груз на некоторую высоту. (рис. 35). Работа совершается за счет энергии нагревателя, передаваемой в форме теплоты. Газ совершает направленное движение, перемещая поршень с грузом, поэтому работа является макрофизической формой обмена энергией системы и окружающей среды.
Рассмотрим работу расширения (или сжатия), совершаемую идеальным газом.
Работа изобарного расширения (р = const )
Работа изобарного расширения n моль идеального газа (работа подъема груза на некоторую высоту) осуществляется за счет внешнего источника энергии (нагревателя) в соответствии с уравнением
d Qр = dU + р dV.
Газ, находящийся в цилиндре под поршнем, изменяет внутреннюю энергию (нагревается) и совершает работу. При р = const нагревание газа сопровождается изменением объема от V1 до V2. Модель такого процесса представлена на рис. 35. Интегрируем уравнение dA = p dV
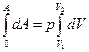
А = р (V2 – V1). (4.18)
Графически в координатах р – V работа изобарного расширения представлена площадью (рис. 38).
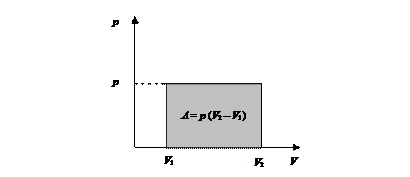
Рис. 38. Работа изобарного расширения
Для n моль исходное и конечное состояния идеального газа выражаются уравнениями.
PV1 = nRT1 и PV2 = nRT2.
Заменим объемы в уравнении (4.18), тогда
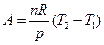. (4.19)
Из уравнений (4.18) и (4.19) следует, что работа расширения идеального газа при постоянном давлении есть функция состояния. Она определяется только начальным и конечным состояниями системы. В данном случае начальное и конечное состояния определяются значениями V и T .
Работа изотермического расширения (Т = const )
Работа изотермического расширения n моль идеального газа также осуществляется за счет внешнего источника энергии (нагревателя, или термостата), но при этом изменяется давление в системе так, как это представлено на рис. 39. Внутренняя энергия идеального газа является функцией температуры. При Т = const dU = 0, и уравнение первого закона термодинамики принимает вид:
d Q = р dV
 |
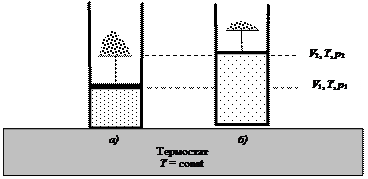Рис. 39. Расширение газа по мере уменьшения груза (количества песчинок) на поршне: а) исходное состояние; б) конечное состояние системы
Интегрируем уравнение dA = p dV
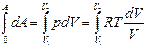
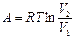(4.20)
Графически в координатах р – V работа изотермического расширения представлена площадью, показанной на рис. 40.
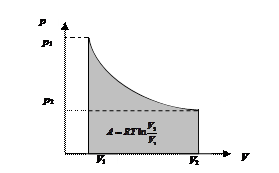
Рис. 40. Работа изотермического расширения
Работа адиабатического расширения ( d Q = 0)
В адиабатическом процессе система обменивается с окружающей средой энергией только в форме работы (d Q = 0), поэтому работа адиабатического расширения осуществляется за счет внутренней энергии n моль идеального газа (рис. 41).
 |
Рис. 41. Адиабатическое расширение (сжатие) идеального газа
При d Q = const уравнение первого закона термодинамики принимает вид:
0 = dU + d А.
Так как работа расширения в адиабатическом процессе происходит за счет уменьшения внутренней энергии системы, то при расширении газ охлаждается, при сжатии – разогревается.
Из уравнения (4.13) dU = n CVdT, тогда
d А = - nCVdT
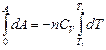
А = n С V(Т1 – Т2) (4.21)
В координатах p – V уравнения изотермы и адиабаты имеют вид р V = const и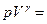 
const соответственно, где 
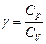. Графически в координатах р – V работа адиабатического расширения представлена площадью, изображенной на рис. 42.
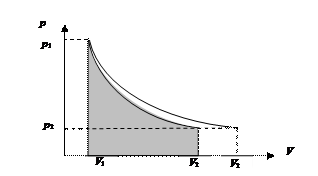
Рис. 42. Работа адиабатического расширения (закрашенная область) меньше, чем работа изотермического расширения в одной и той же области изменений давления
Для изохорного процесса (V = const) работа расширения равна А = 0.
4.4. Применение первого закона термодинамики
к химическим процессам
Любая химическая реакция сопровождается выделением или поглощением энергии. Потенциальная энергия, скрытая в химических связях, и кинетическая энергия (поступательного и других видов движения атомов и молекул) изменяются в ходе химической реакции.
Химическая реакция как система получает энергию извне на разрыв химических связей исходных реагентов и выделяет энергию в окружающую среду при образовании новых химических связей в молекулах – продуктах реакции (табл. 3).
Представим энергетические изменения на примере горения водорода в кислороде (рис. 43).
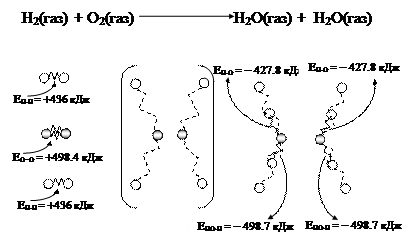Рис. 43. Модель превращения потенциальной энергии, скрытой в химических связях, в кинетическую энергию на примере появления интенсивного колебательного движения молекул – продуктов реакции
При образовании новых химических связей энергия выделяется. Это кинетическая энергия движения молекул – продуктов реакции. Часть внутренней энергии, которая была скрыта в химических связях молекул водорода и кислорода, превратилась в энергию поступательного и других видов движения молекул воды:
D Н =2×(+436)+498.4 + 2×(-427,8) +2×(-498.7) = -482,6 кДж.
Величина D Н = -482,6 кДж эквивалентна энергии движущихся молекул воды. Именно эта кинетическая энергия определяет рост температуры в процессе горения водорода в среде кислорода.
Т а б л и ц а 3