Теплота Q есть форма передачи энергии от одного тела другому посредством соударения микрочастиц, составляющих тела (рис. 37).
Интенсивное движение микрочастиц от горячего к холодному телу распространяется через границу прижатых друг к другу тел. Теплота является микрофизической характеристикой процесса передачи энергии. Если контакта между телами нет и нет никакого посредника для передачи кинетической энергии, следовательно нет соударений между микрочастицами тел и Q = 0.
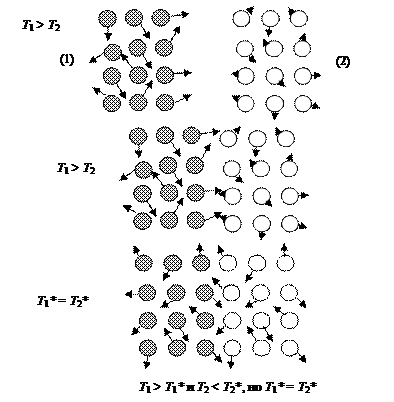
Рис. 37. Модель обмена энергией в форме теплоты (соударения микрочастиц) горячего (система 1) и холодного (система 2) тел
Несложно вычислить теплоту Q, которая необходима для нагревания тела от температуры Т1 до температуры Т2 Для этого необходимо иметь сведения о средней теплоемкости тела. Средняя теплоемкость С – это количество энергии в форме теплоты, затраченное на нагревание одного моля или одного грамма вещества на 1 К. Из определения следует
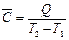или Q = 
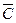(T2 – Т1)
Теплоемкость
Запишем уравнение первого закона термодинамики для бесконечно малого изменения состояния системы
d Q = dU + d А (4.9)
dU является функцией состояния, а d Q и d А не являются функциями состояния системы. Они являются характеристиками процесса. Если нет процесса, то работа и теплота равны нулю.
В термодинамике большую роль играют круговые процессы - циклы. В двигателе внутреннего сгорания, в паровой машине совершаются такие циклы, позволяющие получить работу в тепловом процессе сжигания топлива.
Если единственной работой является работа расширения идеального газа, вычисляемая по уравнению
dA = p dV , (4.10)
то уравнение первого закона термодинамики примет вид
d Q = dU + р dV . (4.11)
Введем понятие истинная теплоемкость при постоянном объеме и постоянном давлении.
При постоянном объеме (V = const) dV=0 и
d Q V = dU , (4.12)
и мы получим выражение теплоемкости при постоянном объеме
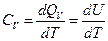. (4.13)
Запишем уравнение первого закона термодинамики при р = const
dQp = dU + р dV (4.14)
dQp = d ( U + р V)
dQp = d Н, (4.15)
где H – энтальпия химической реакции H = (U + pV). Из уравнения (4.15) выражение теплоемкости при постоянном давлении
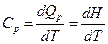. (4.16)
Отметим, что единственный случай, когда теплота физико-химического процесса является функцией состояния, то есть определяется начальным и конечным состояниями системы, отражена в уравнениях (4.12) и (4.15).
Величины удельной и мольной теплоемкости индивидуальных соединений имеют размерности [Дж/г×К] и [Дж/моль×К] соответственно. Между мольными теплоемкостями идеального газа при постоянном давлении и объеме существует связь. Её можно получить из уравнения (4.16):
.
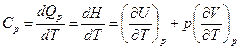Поскольку внутренняя энергия идеального газа не зависит от давления и объема,
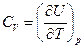и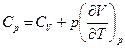 
.
Используя уравнение состояния идеального газа, найдем, что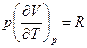 
, тогда
Ср = С V + R . (4.17)
Газовая постоянная R = 8.314 Дж/моль К имеет ту же размерность, что и мольная теплоемкость.
Пример. Вычислим количество энергии, которое необходимо для нагревания 1 г воды (Ср = 4.18 Дж/г К) и 1 г железа (Ср = 0.448 Дж/г К) – от 25 до 100 0С.
Решение
dQ = Ср×dT
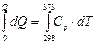
Q = Ср (Т2 – Т1 )
Q (Н2О) = 4.18 (373 – 298) = 313.5 [Дж/г×К]
Q (Fe) = 0.448 (373 – 298) = 33.6 [Дж/г×К].
Не случайно в жаркий солнечный день одинаковые по площади и массе водные и металлические поверхности по-разному нагреваются.
Работа