Под состоянием термодинамического равновесия следует понимать такое состояние системы, свойства которой не обнаруживают заметных изменений в течение времени.
Окружающая среда есть то, что находится вне границ системы и взаимодействует с нею.
Три закона или начала термодинамики лежат в основе всех расчетов свойств систем. К ним добавляют так называемый нулевой закон или закон термического равновесия, опирающийся на понятие «температура» системы. Понятие «температура» господствует над всем учением о теплоте, поэтому, прежде чем давать формулировку закона термического равновесия, рассмотрим физический смысл понятия «температура». Для этого обратимся к разработке метода, позволившего характеризовать термодинамическую температуру числом.
4.1. Закон термического равновесия
Для одноатомных газов кинетическая энергия есть энергия поступательного движения. Из классической механики известно, что энергия поступательного движения частицы определяется её скоростью и массой.
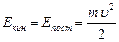, (4.1)
где m – усредненная масса и u – средняя скорость движения атомов.
Из статистической физики следует, что средняя кинетическая энергия частицы, обладающей только поступательным движением, прямо пропорциональна свойству системы – температуре Т.
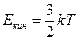, (4.2)
где k – постоянная Больцмана; T – абсолютная температура.
Совместное решение уравнений (4.1) и (4.2) приводит к выражению абсолютной температуры как величины, прямо пропорциональной средней кинетической энергии микрочастиц системы
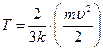. (4.3)
Для таких объектов, как атомы, например атомы инертных (благородных) газов, температура определяется энергией поступательного движения. В случае многоатомных молекул кинетическая энергия включает энергию различных видов движения. Представим модель трехатомной молекулы в виде шариков, связанных пружинками. Для такой молекулы характерна энергия поступательного, колебательного движения атомов в молекуле, а также вращательного и деформационного движения (рис. 33).
Екин. = Епост. + Еколеб. + Евращ. + Едеформ.
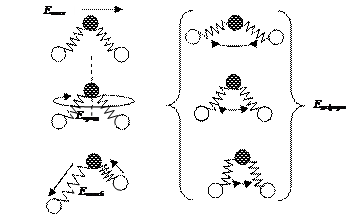
Рис. 33. Формы движения трехатомной молекулы
Для системы, состоящей из громадного числа микрочастиц разной массы и совершающих разнообразные движения, а не только поступательное движение, температура системы является отражением всех форм движения частиц и абсолютная температура системы Т определяется средней кинетической энергией микрочастиц.
Рассмотрим построение термометрической шкалы на примере расширения – сжатия газа. Для идеального газа характерны два свойства: 1) объем молекул газа, много меньше объема, занятого всем газом; 2) радиус взаимодействия двух молекул значительно меньше среднего расстояния между ними.
Идеальных газов как таковых не существует, но можно взять инертный газ или молекулярный азот. Они с успехом выполняют функцию идеального газа.
Заполним газом сосуд постоянного объема (V = const). Измерим давление газа (р2) в сосуде при температуре кипящей воды (Т2) и давление газа (р1) при температуре таящего льда (Т1). При постоянном атмосферном давлении
(р = 1 атм) эксперимент всегда дает одно и то же отношение давлений газа в кипящей воде и плавящемся льду:
.
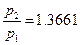Сделаем первое допущение, примем, что отношение давлений прямо пропорционально отношению температур
,
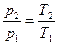тогда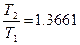 
. (4.4)
Введем второе допущение, примем, что разность температур Т1 и Т2 равна 100
Т2 – Т1 = 100. (4.5)
Совместное решение уравнений (4.4) и (4.5) позволяет установить численное значение температуры кипения воды и плавления льда по так называемой абсолютной шкале температур. Температура кипения воды Т2 = 373.15 К, а температура плавления льда Т1 = 273.15 К. Абсолютная шкала температур всегда положительна. Она введена английским физиком У. Томсоном (лордом Кельвином).