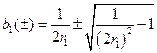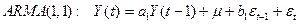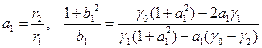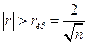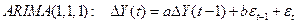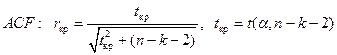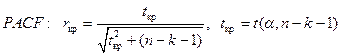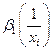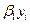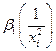Кузнецов Е.Н. Вопросы к экзамену по курсу «ЭКОНОМЕТРИКА» ВАВТ. 2012 (1/4)
(для студентов ФЭМ д/о 3 курс)
I. Теоретические вопросы.
1. Эконометрика и ее типовые задачи. Эконометрическая модель. Случайные возмущения. Типы моделей и типы данных в эконометрике.
2. Суть задачи линейного регрессионного анализа. Парная линейная регрессия. Метод наименьших квадратов. Вывод формул коэффициентов. Интерпретация коэффициентов.
3. Коэффициент ковариации. Коэффициент корреляции. Их свойства. Выборочные оценки и свойства основных числовых характеристик случайных величин. Проверка значимости коэффициента корреляции.
4. Основные свойства точечных оценок. Теорема Гаусса-Маркова (классические условия регрессионного анализа) для одномерной модели (без доказательства).
5. Качество регрессионной модели. Характеристики точности модели. Суммы квадратов. Коэффициент детерминации. Его свойства. Оценка дисперсии случайных возмущений и стандартные ошибки.
6. Проверка гипотез в одномерной модели. Значимость коэффициентов и модели «в целом». Доверительные интервалы. Проверка гипотезы о произвольном значении коэффициента регрессии.
7. Интервальные оценки в эконометрике. Доверительные интервалы математического ожидания, дисперсии, коэффициентов регрессии, прогноза зависимой переменной.
8. Множественная линейная регрессия (КНЛММР). Формы записи модели множественной регрессии (включая матричную). Метод наименьших квадратов. Интерпретация коэффициентов.
9. Множественная регрессия (КНЛММР). Метод наименьших квадратов. Теорема Гаусса-Маркова (классические условия регрессионного анализа) для многомерной модели (без доказательства).
10. Характеристики точности многомерной модели. Суммы квадратов. Коэффициент детерминации. Его свойства. Нормированный коэффициент детерминации. Выбор лучшей модели по R2adj. Оценка дисперсии случайных возмущений и стандартные ошибки.
11. Исследование многомерной регрессионной модели. Гипотеза «Длинная–короткая» модель. Спецификация модели. Исключение существенной переменной. Включение несущественной переменной. Пошаговая регрессия.
12. Исследование многомерной регрессионной модели. Спецификация модели. Выбор из двух линейных моделей. J-тест. Пошаговая регрессия.
13. Исследование многомерной регрессионной модели. Проверка однородности данных – тест Чоу на наличие структурного сдвига. Отличия двух моделей. Примеры. Двойные графики.
14. Качественные переменные в регрессионном анализе. Индикаторные (фиктивные) переменные сдвига и наклона. Интерпретация коэффициентов. Применение фиктивных переменных для учета сезонности.
15. Стохастические регрессоры. Обобщенный метод наименьших квадратов. Теорема Айткена.
16. Гетероскедастичность: природа, последствия, способы обнаружения, средства преодоления.
17. Гетероскедастичность. Метод взвешенных наименьших квадратов. Коррекция моделей на гетероскедастичность (3 случая).
18. Проверка на гетероскедастичность (тесты Гольфельда-Куандта, Бреуша-Пагана и Уайта – три вопроса).
19. Мультиколлинеарность: природа, последствия, способы обнаружения, средства преодоления. Тест Фаррара-Глобера.
20. Частный коэффициент корреляции. Его свойства. Процедура вычисления. Значимость.
21. Автокорреляция остатков: последствия, способы обнаружения, средства преодоления.
22. Обнаружение автокорреляции (Тесты Дарбина-Уотсона и Бреуша-Годфри – два вопроса).
23. Оценивание моделей с автокорреляцией
(2 случая). Процедура Кохрейна-Оркатта.
24. Нелинейные модели регрессии (различные виды моделей и способы их линеаризации). Примеры нелинейных моделей. Роль свободного члена в модели. Интерпретация коэффициентов.
25. Наклон и эластичность. Двойная и полулогариф-мические формы. Интерпретация коэффициентов нелинейной модели. Функция Кобба-Дугласа.
26. Сравнение и выбор нелинейной модели. Тест Зарембки или MWD. Метод Бокса-Кокса.
27. Временные ряды. Факторы, влияющие на формирование значений временного ряда. Структура временного ряда. Основные задачи анализа временных рядов. Роль графического анализа. Исследование временного ряда.
28. Стационарные временные ряды. Их характеристики. «Белый шум». Проверка стационарности временного ряда при помощи критерия серий.
29. Выравнивание временного ряда (аналитическое – выделение тренда регрессией от номера наблюдения, механические – метод последовательных разностей, метод скользящего среднего). Тест Аббе-Линника.
30. Коэффициенты автоковариации и автокорреляции. Способ вычисления. Автокорреляционная функция. Коррелограмма. «Доверительная трубка».
31. Линейные модели стационарных временных рядов (авторегрессии и скользящего среднего).
32. Модель авторегрессии AR(1). Расчет параметров. Прогноз по модели.
33. Модель авторегрессии AR(2). Расчет параметров.
34. Модель авторегрессии AR(p). Уравнения Юла-Уокера.
35. Модель скользящего среднего MA(1). Расчет параметров. Прогноз по модели.
36. Частная автокорреляционная функция. Модели ARMA(p,q). Свойства ACF и PACF.
37. Модели ARIMA(p,d,q). Методология Бокса–Дженкинса. Интерпретация функций АКФ и ЧАКФ.
II. Вопросы для практического анализа и анализа на компьютере.
1. Ручной (табличный) расчет точечных оценок основных числовых характеристик случайных величин (математического ожидания, дисперсии, стандартного отклонения, ковариации, коэффициента корреляции).
2. Ручной (табличный) расчет интервальных оценок основных числовых характеристик случайных величин (математического ожидания, дисперсии) – доверительные интервалы.
3. Ручной (табличный) расчет коэффициентов парной регрессии.
4. Ручной (табличный) расчет коэффициента детерминации парной регрессии.
5. Ручной (табличный) расчет выборочной остаточной дисперсии и стандартных ошибок коэффициентов парной регрессии.
6. Точечный и интервальный прогноз значений зависимой переменной. Прогноз среднего и индивидуального расчетных значений.
7. Вариабельность переменных в регрессионном анализе (расчет коэффициентов вариации).
8. Диаграммы рассеяния в регрессионном анализе.
9. Доказать, что средний остаток в парной регрессии равен нулю.
10. Доказать, что среднее наблюдаемых значений и среднее расчетных значений зависимой переменной в парной регрессии равны между собой.
11. Доказать, что ковариация между столбцом расчетных значений зависимой переменной и столбцом остатков равна нулю.
12. Доказать основное соотношение дисперсионного анализа.
13. Проверка гипотезы равенства нулю отдельных коэффициентов регрессионной модели (значимость коэффициентов).
14. Доверительные интервалы для коэффициентов регрессии (в том числе, ручной расчет). Проверка гипотезы о произвольном значении коэффициента регрессии.
15. Проверка гипотезы равенства нулю всех коэффициентов множественной линейной регрессии, кроме константы (значимость «в целом»).
16. Проверка гипотезы равенства нулю последних 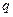 коэффициентов регрессии (гипотеза «длинная–короткая» модель).
коэффициентов регрессии (гипотеза «длинная–короткая» модель).
17. Коэффициент детерминации. Определение спецификации модели по нормированному коэффициенту детерминации.
18. Тест Чоу на однородность данных.
19. Качественные переменные в модели множественной регрессии (индикаторные, фиктивные – dummy переменные). Двойные графики. Интерпретация коэффициентов.
20. Фиктивные переменные наклона (взаимодействия). Двойные графики. Интерпретация коэффициентов. Выбор модели.
21. Тест Гольдфельдта-Куандта.
22. Тест Бреуша-Пагана.
23. Тест Уайта.
24. Тест Дарбина-Уотсона.
25. Тест Бреуша-Годфри.
26. Тест Фаррара-Глобера.
27. Частный коэффициент корреляции.
28. Нелинейная регрессия. Выбор лучшей модели.
29. Тест Зарембки или MWD.
30. Критерий серий для проверки гипотезы о неизменности среднего значения временного ряда.
31. Выделение неслучайной составляющей временного ряда (аналитическое выравнивание). Выбор модели.
32. Выравнивание временного ряда методом последовательных разностей. Тест Аббе-Линника.
33. Автокорреляционная функция.
34. Частная автокорреляционная функция.
35. Модель AR(1).
36. Модель AR(2).
37. Модель МA(1).
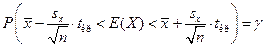
| 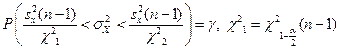
|
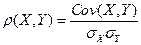
| 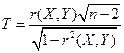 , , 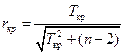
|
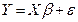 , , 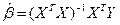
| 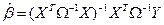
|
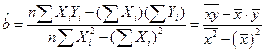
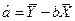
| 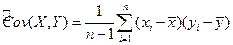
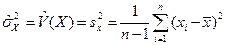
|
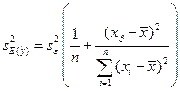
| 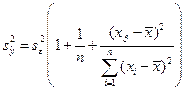
|
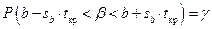
| 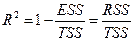 , , 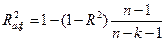
|
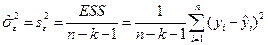
| 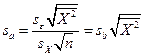 , , 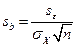 , , 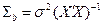
|
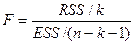 ~ ~ 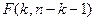
| 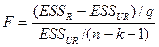 ~ ~ 
|
 ~ ~ 
| 
|
 , ,  ~ ~ 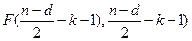
| 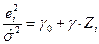 , , 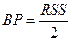 ~ ~ 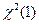
|
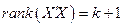 , , 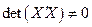
| 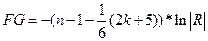 ~ ~ 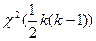
|
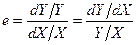
| 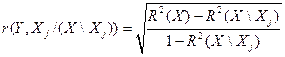
|
|
| |
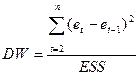 , , 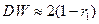
| 
|
|
|
| ||
|
|
| ||
|
|
| ||
|
|
| ||
|
|
| ||
|
|
| ||
|
|
| ||
|
|
| ||
|
| 
| |
|
| 
| |
|
| 
| |
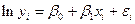
|
| 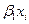
| |
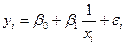
|
| 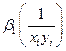
| |









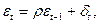
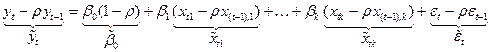
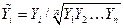 ,
, 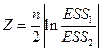 ~
~ 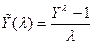
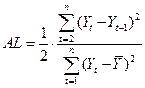
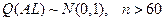
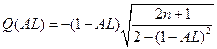
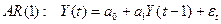
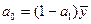 ,
, 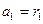 ,
, 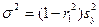
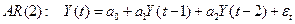
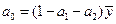 ,
, 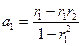 ,
, 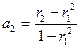
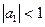
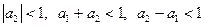
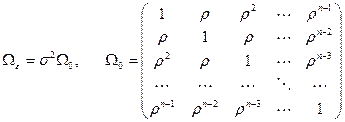
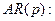
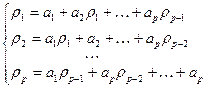
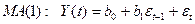 ,
, 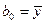 ,
, 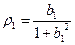 ,
, 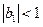 :
: 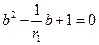 :
: