2. Теорема о дифференцируемости сложной и скалярной функциях нескольких переменных.
Модуль 1. Интегралы
- Вывести формулу объёма тела, образованного вращением вокруг оси Ох фигуры, ограниченной графиками…
- Абсолютная и условная сходимость несобственных интегралов I рода. Критерий Коши сходимости несобственных интегралов I рода. Признак сравнения.
- Доказать аддитивность определённого интеграла.
- Определённый интеграл Римана. Доказать интегрируемость кусочно-непрерывной функции на отрезке.
- Вывести формулу объёма тела, полученного вращением вокруг оси Ох криволинейного сектора, заданного в полярных координатах.
- Верхняя и нижняя суммы Дарбу и их свойства. Верхние и нижние интегралы Дарбу.
- Первообразная. Доказать теорему о множестве первообразных для непрерывной функции. Неберущиеся интегралы.
- Вывести формулу площади фигуры, ограниченной графиками и вертикальными прямыми.
- Длинна плоской кривой. Вывести формулу длинны гладкой кривой, заданной в декартовой и полярной системах координат.
- Доказать теорему о замене переменной в неопределённом интеграле.
- Вывести формулу интегрирования по частям для неопределённого и определённого интегралов.
- Вывести формулы площадей плоских фигур, ограниченных кривыми, заданными в декартовой системе координат.
- Интеграл с переменным верхним пределом. Теорема о производной от интеграла по его верхнему пределу. Формула Ньютона-Лейбница.
- Абсолютная и условная сходимости несобственных интегралов II рода. Критерий Коши сходимости несобственных интегралов II рода. Признаки сравнения.
- Основные свойства определённого интеграла. Доказать линейность и аддитивность определённого интеграла.
- Вывести формулу площади петли, самопересекающейся гладкой кривой на плоскости.
- Несобственный интеграл II рода от неограниченной функции на конечном промежутке. Сходимость и расходимость. Рассмотреть интеграл степенной функции на отрезке [0;1].
- Основные свойства определённого интеграла. Доказать теорему об оценке модуля определённого интеграла.
- Вывести формулу объёма тела, образованного вращением вокруг оси Оу фигуры, ограниченной графиком и вертикальными прямыми.
- Свойство определённого интеграла. Доказать свойство монотонности определённого интеграла. Оценка сверху и снизу и теорема “О среднем”.
- Верхний и нижний интегралы Дарбу. Критерий Дарбу интегрируемости функции.
- Вывести формулу площади поверхности, образованной вращением плоской кривой, заданной в полярной системе координат.
- Вывести формулу площади криволинейного сектора, заданного в полярной системе координат.
- Несобственный интеграл I рода от непрерывной функции на бесконечном промежутке. Сходимость и расходимость. Рассмотреть интеграл степенной функции на промежутке [1;
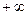 ].
].
Модуль 2. Функции Нескольких переменных
1. Дифференцируемость скалярной функции векторного аргумента. Доказать достаточное условие дифференцируемости.
2. Теорема о дифференцируемости сложной и скалярной функциях нескольких переменных.
3. Полный дифференциал скалярной функции нескольких переменных. Свойства инвариантности.
4. Экстремум скалярной функции векторного аргумента. Доказать теорему о достаточном условии экстремума для дважды дифференцируемой функции.
5. Формула Тейлора для скалярной функции векторного аргумента с остаточным членом в форме Пеано.
6. Касательная плоскость и нормаль к поверхности. Уравнение касательной плоскости и нормали к поверхности, заданной уравнением F(x,y,z)=С.
7. Условный экстремум скалярной функции векторного аргумента. Доказать теорему о достаточном условии условного экстремума для дважды дифференцируемой функции.
8. Доказать теорему о непрерывности сложной функции нескольких переменных.
9. Производная по направлению скалярной функции векторного аргумента (как же он уёбищно говорит слово “функции”, не могу больше это держать в себе). Доказать достаточное условие существования производной по всем направлениям.
10. Окрестности. Внутренние и граничные точки. Открытые и замкнутые множества. Сходимость последовательностей в n-мерном пространстве.
11. Свойство непрерывной функции на компактном множестве.
12. Частные производные высших порядков от скалярной функции. Доказать теорему о независимости смешанных производных от порядка дифференцирования.
13. Экстремум скалярной функции векторного аргумента. Доказать теорему о необходимом условии существования экстремума.
14. Теорема о существовании неявно заданной скалярной функции. Формулы для производных от неявно заданной скалярной функции.
15. Условный экстремум скалярной функции векторного аргумента. Доказать теорему о необходимом существовании условного экстремума.
16. Касательная плоскость и нормаль к поверхности. Уравнение касательной плоскости и нормали к поверхности, заданной уравнением F(x,y,z)=0.
17. Теорема о дифференцируемости сложной векторной функции многих переменных.
18. Предел векторной функции векторного аргумента. Доказать теорему о связи пределов векторной функции векторного аргумента и её координатных функций.
19. Дифференцируемость векторных функций векторного аргумента. Связь с дифференцируемостью координатных функций.
20. Доказать, что для дважды дифференцируемой функции вторые частные производные, которые непрерывны в точке А выполнено: 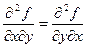 .
.
21. Дифференциал k-го порядка скалярной функции многих переменных. Получить матричную форму записи дифференциала второго порядка (матрица Гессе).
22. Связные множества в n-мерном пространстве. Теорема о промежуточных значениях непрерывной функции.
23. Дифференцируемость скалярной функции нескольких переменных. Доказать, что из дифференцируемости следует непрерывность.
24. Формула Тейлора для скалярной функции векторного аргумента с остаточным членом в форме Лагранжа.
Лекции по Интегралам: http://baumo.narod.ru/MA2.pdf
Лекции по ФНП: http://baumo.narod.ru/Fxyz.pdf








