Вопросы к билетам по материалу III -го семестра для студентов ФИБС
1. Законы геометрической оптики.
2. Уравнение волны. Плоская и сферическая волны.
3. Энергия плоской волны. Объемная плотность энергии. Поток энергии. Плотность потока энергии волн. Вектор Умова.
4. Групповая скорость пакета волн. Принцип суперпозиции волн.
5. Волновое уравнение для векторов электромагнитного поля.
6. Скорость распространения волны.
7. Поляризация электромагнитных волн.
8. Вектор Пойнтинга.
9. Движущиеся источники колебаний и эффект Доплера. Эффект Доплера в оптике.
10. Интерференция от двух когерентных источников.
11. Методы получения когерентных источников.
12. Интерференция в тонких пленках.
13. Полосы равной толщины и равного наклона.
14. Просветление оптики.
15. Дифракция. Принцип Гюйгенса-Френеля.
16. Зоны Френеля.
17. Дифракция от щели.
18. Дифракциооная решетка.
19. Разрешающая способность оптических приборов.
20. Поляризация света. Поляризаторы.
21. Поляризация при отражении и преломлении. Закон Брюстера.
22. Анизотропные среды. Двойное лучепреломление.
23. Искусственное двойное лучепреломление. Эффект Керра.
24. Естественная оптическая активность. Эффект Фарадея.
25. Тепловое излучение. Равновесное тепловое излучение. Закон Кирхгофа.
26. Закон Стефана-Больцмана.
27. Закон Вина.
28. Спектральное распределение для равновесного теплового излучения.
29. Формула Рэлея-Джинса.
30. «Ультрафиолетовая катастрофа».
31. Формула Планка.
32. Понятие об оптической пирометрии. Поток излучения. Энергетическая освещенность. Энергетическая сила света. Энергетическая яркость. Спектральная плотность энергетической яркости. Радиационная , яркостная, цветовая температуры.
33. Квантовая природа света. Фотоэффект.
34. Законы Столетова. Основное уравнение внешнего фотоэффекта.
35. Взаимодействие света с веществом. Давление света. Опыты Лебедева.
36. Элементы квантовой механики. Постулаты Бора.
37. Волны де-Бройля. Дифракция электронов.
38. Опыты Дэвиссона и Джермера.
39. Волновая функция.
40. Соотношение неопределенностей Гейзенберга.
41. Уравнение Шредингера. Движение свободной частицы.
42. Частица в потенциальной яме.
43. Прохождение частицы сквозь потенциальный барьер. Коэффициенты отражения и прохождения (прозрачности). Туннельный эффект.
44. Атом водорода. Квантовые числа.
45. Правило отбора.
46. Опыты Штерна и Герлаха. Спиновое квантовое число.
47. Магнетон Бора.
48. Орбитальное и спиновое гиромагнитные отношения.
49. Эффект Зеемана. Теорема Лармора.
50. Магнитный резонанс.
51. Вынужденное и самопроизвольное излучение.
52. Термоядерные реакции.
53. Энергия связи и ядерные силы.
54. Модели ядра.
55. Радиоактивность. Радиоактивное излучение.
56. Закон радиоактивного распада. Альфа- распад. Бета –распад. Гамма-излучение.
57. Ядерные реакции.
58. Деление ядер.
Задачи
Волны в упругой среде
1. Определить разность фаз Dj колебаний источника волн, находящегося в упругой среде, и точки этой среды, отстоящей на 2 см от источника. Частота колебаний n = 5 Гц, скорость распространения волн v = 40м/с.
2. Волны распространяются в упругой среде со скоростью V = 100 м/с. Наименьшее расстояние между точками среды, фазы Dj колебаний которых противоположны, равно 1 м. Определить частоту n колебаний.
3. Определить скорость распространения волны в упругой среде, если разность фаз Dj колебаний двух точек среды, отстоящих друг от друга на Dx = 10 см, равна 600. Частота колебаний n = 25 Гц.
4. От источника колебаний распространяются волны вдоль прямой линии. Амплитуда колебаний А = 10 см. Как велико смещение ξ точки, удаленной от источника на ¾ длины волны в момент, когда от начала колебаний источника прошло время t = 0,9 периода колебаний?
5. Волны с периодом Т = 1,2 с и амплитудой А = 2 см распространяется со скоростью v = 15м/с. Чему равно ξ смещение точки, находящейся на расстоянии x = 45 см от источника волн в тот момент, когда от начала колебаний источника прошло время t = 4 с?
6. Две точки находятся на одной прямой, вдоль которой распространяются волны со скоростью v = 50 м/с. Период колебаний Т = 0,05 с. Расстояние между точками x = 50 см. Найти разность фаз Dj колебаний в этих точках.
Интерференция
1. Два точечных когерентных источника света находятся в спирте (n=1,36) на расстоянии 1 см друг от друга. Определить оптическую разность хода для точки, лежащей на расстоянии 20 см от одного источника по направлению нормали к прямой, соединяющей источники.
2. Вычислить длину световой волны в опыте с зеркалами Френеля, если расстояние между мнимыми источниками света равно 1,37 мм, расстояние источников до экрана равно 2 м. На экране получаются темные и светлые полосы, расстояние между соседними темными полосами равно 0,8 мм.
3. Найти расстояние между интерференционными полосами в опыте с зеркалами Френеля, если экран находится на расстоянии а = 2 м от линии пересечения зеркал. Угол между зеркалами a = 179040’ и расстояние от источника до линии пересечения зеркал r = 10 см. длина световой волны l = 569 нм.
4. Вычислить наименьшую толщину мыльной пленки с показателем преломления n = 1,33, при которой станет видна интерференционная картина. На пленку падает свет с длиной волны l = 0,6 мкм, а наблюдение ведется в отраженном свете.
5. Найти показатель преломления жидкости, заполняющей пространство между стеклянной пластинкой и лежащей на ней плосковыпуклой линзой, если при наблюдении в отраженном свете l = 0,6 мкм радиус десятого темного кольца Ньютона оказался равным 2,1 мм. Радиус кривизны линзы R = 1м.
6. Тонкая проволочка лежит между двумя стеклянными плоскопараллельными пластинками параллельно линии их соприкосновения, вследствие чего в отраженном свете наблюдается интерференционная картина с расстоянием между соседними полосами Dx = 1,5 мм. Проволочка расположена на расстоянии L = 7,5 см от линии соприкосновения пластин и имеет диаметр D = 0,01 мм. Определить длину волны падающего света.
7. Найти фокусное расстояние плосковыпуклой линзы, примененной для наблюдения колец Ньютона, если радиус третьего светлого кольца равен 1,1 мм, показатель преломления стекла линзы 1,6, длина световой волны l = 589 нм. Наблюдение ведется в отраженном свете.
8. На стеклянный клин с показателем преломления n = 1,5 нормально к его грани падает монохроматический свет с длиной волны l = 600 нм. Число интерференционных полос, наблюдаемых на 1 см, равно 10. Найти преломляющий угол клина.
Дифракция
1. На круглое отверстие диаметром 4 мм нормально падает параллельный пучок монохроматического света с длиной волны l = 500 нм. Точка наблюдения находится на расстоянии 1 м от отверстия на его оси. Сколько зон Френеля укладывается в отверстии?
2. Пучок монохроматического света с длиной волны l = 546 нм падает нормально на щель. Определите ширину щели, если первый дифракционный максимум наблюдается под углом 20.
3. На плоскую дифракционную решетку, постоянная которой (a+b)= 4*10-4 см, нормально падает пучок белого света. Определить протяженность видмого участка спектра 1-го порядка, спроектированного на экран линзой с фокусным расстоянием F = 50 см. Принять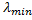 
=380 нм и 
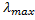=760 нм.
4. На плоскую дифракционную решетку, имеющую 200 штрихов на 1 мм, нормально падает параллельный пучок света от разрядной трубки с криптоном. Под каким углом в поле зрения совпадут линии криптон с длинами волн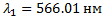 
и 
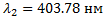? В каких порядках спектра может произойти совпадение?
5. Определить ширину дифракционной решетки, которая позволила бы разрешить в спектре 3-го порядка две линии натрия с длинами волн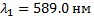 
и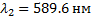 
. Постоянная решетки равна 5 мкм. Ответ: 
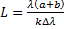=1.63 мм.
Поляризация
1. Во сколько ослабляется естественный свет, проходя через 2 николя, если их плоскости составляют угол 300, а в каждом николе теряется 10% падающего на него светового потока?
2. На стеклянную пластинку с показателем преломления n = 1.54 падает естественный луч света. Определить угол между падающим и отраженным и отраженным лучами, если отраженный максимально поляризован.
3. Луч света, идущий в стеклянном сосуде, наполненном серной кислотой, отражается от поверхности стекла. При каком угле падения отраженный свет полностью поляризован? Показатель преломления кислоты n1=1.43, показатель преломления стекла n2=1.52.
4. Определить, на сколько процентов уменьшится яркость светового пучка после прохождения через призму Николя, если на призму падает естественный свет. Потери энергии, связанные с поглощением и отражением света в николе, составляет 12%.
5. Частично поляризованный свет состоит из естественного и линейно-поляризованного света. Чтобы найти отношение яркостей этих компонент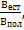 
пучок направляют на николь так, чтобы получить сначала наибольшую Вmax, а затем Вmin яркости выходящего луча. Оказалось 
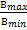=2. Определить отношение яркостей естественного и поляризованного света в падающем пучке.
Тепловое излучение
1. Металлический шар радиусом 1 см и теплоемкостью 14 Дж/К, имеющий температуру 1200 К, помещен в вакуум. Поглощательная способность материала, из которого изготовлен шар, постоянна и равна 0,4. Через сколько времени температура шара уменьшится вдвое?
2. Поток энергии, излучаемой из смотрового окна плавильной печи, равен 34 Вт. Определить температуру печи, если площадь окна 6 см2. На какую длину волны приходится максимум спектральной плотности энергетической светимости печи, если считать ее абсолютно черным излучателем?
3. Какова должна быть температура абсолютно черного тела, чтобы максимум спектральной плотности его энергетической светимости приходился на длину волны 550 нм? Какова при этом его энергетическая светимость?
4. Тело массой 10 г с поверхности 200 см2 имеет температуру 600 К. Поглощательная способность поверхности тела равна 0,4, его удельная теплоемкость 334,4 Дж/(кг К). Найти температуру тела через 30 с, если оно помещено в вакуум, а излучением, падающим на него от окружающих предметов, можно пренебречь.
5. Длина волны, на которую приходится максимум спектральной плотности энергетической светимости АЧТ. Авна550 нм. Найти интегральную энергетическую светимость этого тела.
6. Какую температуру должно иметь тело, чтобы при температуре окружающей среды 290 К оно излучало в 100 раз больше энергии, чем поглощало?
Фотоэффект. Давление света.
1. Определить красную границу фотоэффекта для цезия, если при облучении его поверхности фиолетовыми лучами с длинной волны 400 нм максимальная скорость фотоэлектронов равна 6,5*105 м/с.
2. Железный шарик, отдаленный от других тел, облучают монохроматическим светом с длиной волны 200 нм. Работа выхода электрона из железа равна 4,36 эВ. До какого максимально потенциала зарядится шарик, теряя фотоэлектроны?
3. На платиновую пластинку падают ультрафиолетовые лучи. Для прекращения фотоэффекта нужно приложить задерживающую разность потенциалов 3,7 В. Работа выхода электронов из платины равна 6,3 эВ. Если платину заменить пластиной из другого металла, то задерживающая разность потенциалов увеличиться до 6 В. Определить работу выхода электронов из этого металла.
4. Параллельный пучок монохроматического света с длиной волны 550 нм, падающий на зеркальную поверхность, производит на нее давление 0,3 мкПа. Найти концентрацию фотонов в этом световом пучке.
5. Монохроматическое излучение с длиной волны 500 нм нормально падает на плоскую поверхность с поглощательной способностью 0,4 и давит на неё с силой 10-8 Н. Определить число фотонов, ежесекундно попадающих на эту поверхность.
6. Определить постоянную Планка h, если известно, что электроны, вырываемые с поверхности некоторого металла светом с частотой 2,2*1015 с-1, полностью задерживаются обратным потенциалом 6,6 В, а электроны, вырванные с частотой 4,6*1015 с-1 – потенциалом 16,5 В.
7. Цезий, работы выхода электронов из которого равна 1,88 эВ, освещается монохроматическим светом с длиной волны 476 нм. Какую наименьшую задерживающую разность потенциалов нужно приложить, чтобы фототок полностью прекратился?
Атом водорода. Теория Бора.
1. Атом находится в возбужденном состоянии, характеризуемом главным квантовым числом n=4. Определить возможные спектральные линии в спектре водорода, появляющиеся при переходе атома в основное состояние.
2. Используя теорию Бора, определить орбитальный магнитный момент электрона, движущегося по третьей орбите атома водорода.
3. Определить изменение орбитального механического момента электрона при его переходе из возбужденного состояния в основное с испусканием фотона с длиной волны 102 нм.
4. Найти частоту света, излучаемого атомом водорода, при переходе электрона на уровень с главным квантовым числом n=2, если радиус электрона изменился в 9 раз.
5. Найти квантовое число, соответствующее возбужденному состоянию иона He+ , если при переходе в основное состояние этот ион последовательно испустил два фотона с длинами волн 108,5 нм и 30,4 нм.
Волновые свойства частиц
1. Определить длину волны де-Бройля для электрона, находящегося в атоме водорода на третьей боровской орбите.
2. Заряженная частица, ускоренная разностью потенциалов 500 В, имеет длину волны де-Бройля 1,28 пм. Считая, что заряд частицы равен заряду электрона, найти ее массу.
3. Параллельный пучок моноэнергетических электронов направлен нормально на узкую щель шириной 1 мкм. Найти скорость электронов, если на экране, отстоящем на расстоянии 20 см от щели, ширина центрального дифракционного максимума равна 48 мкм.
4. Электрон находится в одномерной потенциальной яме шириной l с бесконечно высокими стенками во втором возбужденном состоянии. Найти вероятность нахождения электрона в средней трети ямы.
5. Частица с энергией 50 эВ, двигаясь в положительном направлении оси x, попадает на полубесконечный потенциальный барьер высотой 20 эВ. Найти вероятность отражения частицы от этого барьера.
6. Прямоугольный потенциальный барьер имеет ширину 0,1 нм. Разность между высотой барьера и энергией электрона, движущегося в положительном направлении оси x, равна 5 эВ. Во сколько раз изменится коэффициент прозрачности барьера для электрона, если разность энергий возрастает в 4 раза.
7. Найти длину волны де-Бройля для a-частицы, движущейся по окружности радиусом 0,83 см в однородном магнитном поле с индукцией 0,25 Тл.
8. Рассматривая математический маятник как гармонический осциллятор, найти в эВ энергию нулевых колебаний для маятника длиной 1 м, находящегося в поле тяготения Земли.
Одномерная бесконечно глубокая потенциальная яма
1. Электрон находится в потенциальной яме шириной 0,5 нм. Определить наименьшую разность его энергетических уровней.
2. Электрон находится в потенциальной яме шириной l. В каких точках внутри ямы плотность вероятности нахождения электрона на первом и втором энергетических уровнях одинакова? Вычислить значение плотности вероятности для этих точек.
3. Найти вероятность нахождения электрона в средней трети потенциальной ямы, если он находится в первом возбужденном состоянии (n=2).
4. Частица в потенциальной яме находится в основном состоянии. Какова вероятность найти частицу: 1) в средней трети ямы, 2) в крайней трети?
Полубесконечный потенциальный барьер
1. Поток электронов, обладающих энергией 100 эВ, падает на потенциальный барьер. Определить высоту потенциального барьера, если 4 % падающих на барьер электронов отражается.
2. Электрон с энергией 100эВ падает на потенциальный барьер высотой 64 эВ. Определить вероятность того, что электрон отразится от барьера.
3. Вычислить коэффициент прохождения электрона с энергией 100 эВ через потенциальный барьер высотой 99,75 эВ?
4. Электрон обладает энергией 10 эВ. Во сколько раз изменится его скорость после прохождения потенциального барьера высотой 6 эВ?
5. Протон с энергией 1 МэВ изменил при прохождении потенциального барьера дебройлевскую длину волны на 1 %. Определить высоту потенциального барьера.
Потенциальный барьер конечной ширины
1. Электрон с энергией 9 эВ движется в положительном направлении оси x. Оценить вероятность того, что электрон пройдет через потенциальный барьер высотой 10 эВ и шириной 0.1 нм.
2. Найти вероятность прохождения электрона сквозь потенциальный барьер при разности энергий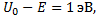 
если ширина барьера: 1) 0,1 нм. 2) 0,5 нм.
3. Электрон проходит сквозь потенциальный барьер шириной 0,5 нм. Высота барера на 1% больше энергии электрона. Найти коэффициент прозрачности, если энергия электрона: 10 эВ, 2) 100 эВ.
4. Ширина прямоугольного потенциального барьера 0,2 нм. Разность высоты барьера и энергии электрона 1 эВ. Во сколько раз изменится вероятность прохождения электроном барьера, если разность возрастет в 10 раз?
5. При какой ширине потенциального барьера коэффициент прозрачности для электрона равен 0,01, если разность энергий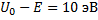 
?.
6. Прямоугольный потенциальный барьер имеет шину 0,1 нм. При какой разности энергий вероятность прохождения электрона через барьер равна 0,99?.
7. Протон и электрон прошли одинаковую ускоряющую разность потенциалов 10 кэВ. Во сколько раз отличается коэффициенты прозрачности для электрона и протона, если высота барьера 20 кэВ, а его шина 0,1 пм?
Атом водорода
1. Атом водорода находится в основном состоянии. Собственная волновая функция, описывающая состояние электрона в атоме, имеет вид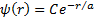 
. Где С – некоторая постоянная, а а – радиус первой боровской орбиты. Из условия нормировки найти значение постоянной С.
2. Электрон находится в атоме водорода в основном состоянии. Найти отношение вероятностей пребывания электрона в сферических слоях толщиной Dr = 0,01 а с радиусами r 1 = 0.5а и r 1 = 1.5а.
3. Вычислить полную энергию, орбитальный момент импульса и магнитный момент электрона, находящегося в атоме водорода в состоянии 2р.
4. Определить возможные значения магнитного момента, обусловленного орбитального движения электрона в возбужденном атоме водорода, если энергия возбуждения 12,09 эВ.
Эффект Зеемана
1. Какова должна быть напряженность магнитного поля, чтобы расщепление спектральной линии с длиной волны 550 нм достигло 0,01 %?
2. Определить величину расщепления спектральной линии с длиной волны 500 нм в магнитном поле с напряженностью 1,59*106 А/м.
3. Для наблюдения эффекта Зеемана источник света помещен в магнитное поле с индукцией 2,0 Тл и рассматривается спектральная линия с длиной волны 422,67 нм. Вычислить разность длин волн для смещенной и несмещенной компонент.
Рентгеновское излучение
1. Определить порядковый номер элемента в таблице Менделеева, если длин волны Ka характеристического излучения составляет 72 пм.
2. Определить постоянную экранирования для L- серии рентгеновского излучения , если при переходе электрона в атом вольфрама (Z=74) с М-оболочки на L-оболочку длина волны испущенного фотона составляет 140 пм.
3. Определить длину волны коротковолновой границы сплошного рентгеновского спектра, если скорость электронов, бомбардирующих антикатод рентгеновской трубки, равна 0,8×с, где с-скорость света в вакууме.