Глава 5.Сравнительный анализ вычислительных методов электродинамики
Вычислительный электромагнетизм (CEM), вычислительная электродинамика или электромагнитное моделирование-это процесс моделирования взаимодействия электромагнитных полей с физическими объектами и окружающей средой.
Обычно это включает в себя использование компьютерных программ для вычисления приближенных решений уравнений Максвелла для расчета характеристик антенны, электромагнитной совместимости, поперечного сечения радара и распространения электромагнитных волн, когда они не находятся в свободном пространстве. Большое подполе-это компьютерная программа для моделирования антенн, которая вычисляет диаграмму направленности и электрические свойства радиоантенн и широко используется для проектирования антенн для конкретных применений.
Некоторые реальные электромагнитные проблемы, такие как электромагнитное рассеяние, электромагнитное излучение, моделирование волноводов и т.д., Не поддаются аналитическому расчету из-за множества нерегулярных геометрий, обнаруженных в реальных устройствах. Вычислительные численные методы могут преодолеть неспособность получить решения уравнений Максвелла в замкнутой форме при различных определяющих соотношениях сред и граничных условиях. Это делает вычислительный электромагнетизм (CEM) важным для проектирования и моделирования антенных, радиолокационных, спутниковых и других систем связи, нанофотонных устройств и высокоскоростной кремниевой электроники, медицинской визуализации, проектирования антенн сотовых телефонов и других приложений.
CEM обычно решает задачу расчета E (электрического) и H (магнитного) полей в проблемной области (например, для расчета диаграммы направленности антенны для произвольной структуры антенны). Кроме того, расчет направления потока мощности( вектора Пойнтинга), нормальных волноводных мод, дисперсии волн, генерируемых средой, и рассеяния может быть рассчитан на основе полей E и H. Модели CEM могут принимать или не принимать симметрию, упрощая реальные структуры до идеализированных цилиндров, сфер и других регулярных геометрических объектов. Модели CEM широко используют симметрию и решают задачу уменьшения размерности с 3 пространственных измерений до 2D и даже 1D.
Формулировка задачи на собственные значения CEM позволяет вычислить стационарные нормальные режимы в структуре. Переходный отклик и эффекты импульсного поля более точно моделируются CEM во временной области с использованием FDTD. Изогнутые геометрические объекты более точно обрабатываются как конечные элементы МКЭ или неортогональные сетки. Метод распространения пучка (BPM) может быть решен для потока мощности в волноводах. CEM зависит от конкретного приложения, даже если различные методы сходятся к одному и тому же полю и распределению мощности в моделируемой области.
5.1.Обзор методов
Один из подходов заключается в дискретизации пространства в терминах сеток (как ортогональных, так и неортогональных) и решении уравнений Максвелла в каждой точке сетки. Выборка потребляет компьютерную память, а решение уравнений занимает значительное время. Крупномасштабные проблемы CEM сталкиваются с ограничениями памяти и ПРОЦЕССОРА. По состоянию на 2007 год проблемы CEM требуют суперкомпьютеров, высокопроизводительных кластеров, векторных процессоров и / или параллелизма. Типичные формулировки включают в себя либо переход с течением времени через уравнения по всей области для каждого момента времени; или использование инверсии полосчатых матриц для вычисления весов базисных функций при моделировании методами конечных элементов; или матричные произведения при использовании методов матриц переноса; или вычисление интегралов при использовании метода моментов (MoM); или использование быстрых преобразований Фурье и временных итераций при вычислении методом разделения шагов или BPM.
Выбор методов. Выбор правильного метода решения проблемы очень важен, так как неправильный выбор может привести либо к неправильным результатам, либо к результатам, которые требуют слишком много времени для расчета. Однако название метода не всегда говорит о том, как он реализован, особенно для коммерческих инструментов, которые часто имеют более одного решателя.
Дэвидсон [1] приводит две таблицы, в которых сравниваются методы FEM, MoM и FDTD, как они обычно реализуются. Одна таблица предназначена как для задач с открытой областью (задачи излучения и рассеяния), так и для задач с управляемой волной.
5.2 Уравнения Максвелла в гиперболической форме PDE
Уравнения Максвелла можно сформулировать как гиперболическую систему уравнений в частных производных. Это дает доступ к мощному методу численных решений.
Предполагается, что волны распространяются в плоскости (x, y) и ограничивают направление магнитного поля, параллельного оси z, и, следовательно, электрического поля, параллельного плоскости (x, y). Эта волна называется поперечной магнитной (ТМ) волной. В 2D и без поляризационных терминов уравнения Максвелла могут быть сформулированы следующим образом:
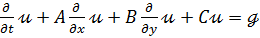 (5.1)
(5.1)
где u, A, B и C определяются как
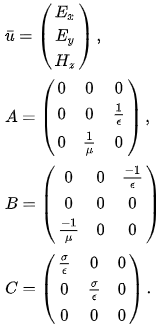 (5.2)
(5.2)
В этом представлении является принудительной функцией и находится в том же пространстве, что и u . Его можно использовать для выражения внешнего поля приложения или для описания ограничения оптимизации. Как указано выше:
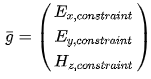 (5.3)
(5.3)
Также может быть явно определено равным нулю для упрощения определенных задач или для нахождения характерного решения, что часто является первым шагом в методе поиска конкретного неоднородного решения.
5.4 Решатели интегральных уравнений. Дискретное дипольное приближение
Дискретная дипольная аппроксимация-это гибкий метод расчета рассеяния и поглощения мишенями произвольной геометрии. Формулировка основана на интегральной форме уравнений Максвелла. ДДА - это аппроксимация цели континуума конечным массивом поляризуемых точек. Точки приобретают дипольные моменты в ответ на локальное электрическое поле. Диполи, конечно, взаимодействуют друг с другом через свои электрические поля, поэтому ДДА также иногда называют связанным дипольным приближением. Полученная линейная система уравнений обычно решается с помощью сопряженных градиентных итераций. Матрица дискретизации имеет симметрии (интегральная форма уравнений Максвелла имеет форму свертки), что позволяет быстрому преобразованию Фурье умножать матрицу на вектор во время итераций сопряженного градиента.
5.5 Метод элементов моментов
Метод моментов (MoM) или метод граничных элементов (BEM) - это численный вычислительный метод для решения линейных дифференциальных уравнений в частных производных, которые были сформулированы как интегральные уравнения (т. Е. в форме граничного интеграла). Он может быть применен во многих областях техники и науки, включая механику жидкости, акустику, электромагнетизм, механику разрушения и пластичность.
БЕМ стал более популярным с 1980-х годов. Поскольку он требует вычисления только граничных значений, а не значений по всему пространству, он значительно более эффективен с вычислительной точки зрения для задач с небольшим отношением поверхности к объему. Концептуально он работает, создавая "сетку" над моделируемой поверхностью. Однако для многих задач БЭМ значительно менее эффективен в вычислительном отношении, чем методы дискретизации объема (метод конечных элементов, метод конечных разностей, метод конечных объемов). Формулировки граничных элементов обычно приводят к полностью заполненным матрицам. Это означает, что требования к хранилищу и вычислительное время будут расти в соответствии с квадратом размера проблемы. Напротив, матрицы конечных элементов, как правило, связаны (элементы связаны только локально), и требования к хранению системных матриц, как правило, линейно растут с размером проблемы. Методы сжатия (такие как мультипольные разложения или адаптивные кросс-аппроксимационные / иерархические матрицы) могут быть использованы для улучшения этих задач, хотя и за счет дополнительной сложности и с вероятностью успеха, которая в значительной степени зависит от характера и геометрии задачи.
БЭМ применим к задачам, для которых могут быть вычислены функции Грина. Они обычно включают поля в линейных однородных средах. Это накладывает существенные ограничения на диапазон и общность задач, подходящих для граничных элементов. Нелинейности могут быть включены в формулировку, хотя они обычно вводят интегралы объема, которые требуют дискретизации объема перед решением, устраняя часто упоминаемое преимущество BEM.
Сравнение результатов моделирования и аналитической формулировки
Например, оценка радиолокационного сечения пластины с использованием аналитической формулы:
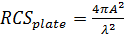 , (5.4)
, (5.4)
где A-поверхность пластины ,- длина волны. В качестве эталонного примера можно использовать следующую кривую, представляющую RCS пластины, рассчитанную на частоте 35 ГГц.
Когда сложность теоретических формул затрудняет решение аналитического решения, мы прибегаем к неаналитическим методам, которые включают графические методы, экспериментальные методы, аналоговые методы и численные методы. Графические, экспериментальные и аналоговые методы могут быть использованы для решения относительно небольшого числа задач. Численные методы приобрели популярность и стали более привлекательными с появлением быстрых цифровых компьютеров. Наиболее часто используемыми простыми численными методами в ЭМ являются метод моментов, метод конечных разностей, метод конечных элементов и метод моделирования заряда. Большинство задач ЭМ связаны либо с уравнениями в частных производных, либо с интегральными уравнениями. Дифференциальные уравнения в частных производных обычно решаются методом конечных разностей или методом конечных элементов; интегральные уравнения удобно решать методом моментов. Хотя численные методы дают приближенные решения, эти решения довольно точны для инженерных целей. У нас не должно сложиться впечатление, что аналитические методы устарели из-за численных методов; скорее, они дополняют друг друга. Каждый численный метод включает в себя аналитическое упрощение до такой степени, что его легко применить.
5.6 Графические методы
Эти методы анализируют данную проблему с использованием различных таблиц и диаграмм, таких как диаграммы линий передачи, диаграммы Смита и так далее. На этих диаграммах показаны вариации проблемы и отмечены соответствующие наблюдения. Их использование ограничено уравнениями Лапласа для двумерных геометрий, поскольку они обычно основаны на свойствах аналитических функций. Существуют некоторые ограничения в графических методах. Их точность ограничена даже при тщательном применении.
Методы моментов
Метод моментов -это мощный вычислительный метод, который частично аналитичен и частично вычислителен. Этот метод очень эффективен для анализа геометрии открытых областей, таких как антенны, рассеиватели и плоские схемы. Метод основан на методе взвешенного остатка, в котором остаток управляющего уравнения устанавливается равным нулю в среднем по области. Неизвестная функция расширяется
в наборе функций разложения, а внутреннее произведение остатка равно нулю. Предполагается, что число тестовых функций равно числу функции декомпозиции, чтобы сгенерировать столько
уравнений, сколько существует неизвестных. MoM иллюстрируется решением ряда примеров, таких как емкость полосовой линии, распределение заряда
на металлической проволоке, распределение тока и входное сопротивление полуволнового диполя и RCS цилиндрического диффузора.
MOM - это метод, используемый для решения электромагнитных граничных или объемных интегральных уравнений в частотной области. Поскольку электромагнитные источники представляют интерес, MOM очень полезен при решении проблемы излучения и рассеяния. Новый метод интеграции, основанный на использовании квази. Предложен метод интегрирования Монте-Карло (QMCI) для метода решения моментов интегрального уравнения для расчета емкости. Сформулировано интегральное уравнение для неизвестного распределения заряда по конденсаторам. Решения получены методом MOM с использованием QMCI метод. Он обеспечивает точный расчет емкостей параллельных пластинчатых, цилиндрических и сферических конденсаторов.
5.7 Метод конечных элементов
Метод конечных элементов берет свое начало в области структурного анализа. Этот метод не применялся к задачам ЭМ до 1968 года. Как и метод конечных разностей, метод конечных элементов полезен при решении дифференциальных уравнений. Метод конечных разностей представляет область решения с использованием массива точек сетки; его применение становится затруднительным из-за проблем с границами неправильной формы. Такие задачи легче решить с помощью метода конечных элементов. Конечно - элементный анализ любого задача состоит в основном из четырех этапов: (а) дискретизация области решения на конечное число элементов, (б) вывод уравнений управления для типичного элемента, (в) сборка всех элементов в области решения и (г) решение результирующей системы уравнений.
Метод моделирования заряда Метод моделирования заряда очень полезен для решения уравнений в частных производных в электротехнике и был изучен и разработан многими исследователями. Этот метод прост для понимания и может быть применен только при решении системы одновременных линейных уравнений. Многие примеры показывают, что метод позволяет получать достаточно точные решения краевых задач относительно областей, ограниченных гладкими кривыми.
5.8 Общий анализ
Значительная работа уже проделана в области расчета пропускной способности. Проанализирована оценка емкости на единицу длины металлического прямоугольного параллелепипеда с диэлектрическим покрытием для геометрии (Prarthana D. Mehta & S. B. Chakrabarty,). Распределение заряда по поверхности металлической грани прямоугольного параллелепипеда и соответствующей грани диэлектрического покрытия для верхней грани показано на рис. 1(а)и (б) соответственно. Валидность анализа это было обосновано сравнением данных о емкости, имеющихся в литературе для металлического куба и полого цилиндра с верхними и нижними накладками, с данными о емкости, рассчитанной этим методом для аналогичных структур, с учетом очень низкой диэлектрической проницаемости, а также очень тонкого диэлектрического покрытия.
Оценка емкости одного куба анализируется с помощью программы MATLAB. Для определения распределения заряда и емкости проводящих структур была разработана компьютерная программа, основанная на предыдущих формулировках. Выбор этой программы основан на ее широкой доступности в университетах и отраслях промышленности и простоте использования. Чтобы использовать метод поддоменов, авторы разделяют общую площадь поверхности a2 одной стороны куба на несколько поддоменов.
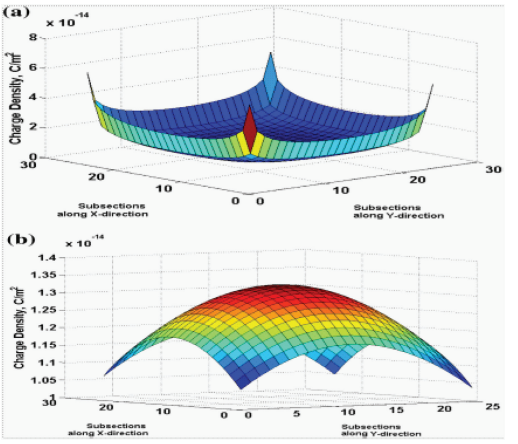
Рис.5.1 Распределение заряда по направлению X-Y (а) верхняя проводящая грань (б) Диэлектрическое покрытие верхней проводящей грани








