ЗАДАНИЕ N 8 отправить сообщение разработчикам Тема: Умножение матриц Умножение матрицы A на матрицу B возможно, если эти матрицы имеют вид …
 ЗАДАНИЕ N 1 отправить сообщение разработчикам
ЗАДАНИЕ N 1 отправить сообщение разработчикам
Тема: Дифференциальное исчисление ФНП
Приближенное значение функции 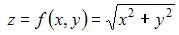 в точке
в точке 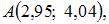 вычисленное с помощью полного дифференциала, равно …
вычисленное с помощью полного дифференциала, равно …

| 5,002 | ||
| 5,02 | |||
| 5,062 | |||
| 5,001 |
 ЗАДАНИЕ N 2 отправить сообщение разработчикам
ЗАДАНИЕ N 2 отправить сообщение разработчикам
Тема: Основные методы интегрирования
Множество первообразных функции 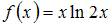 имеет вид …
имеет вид …

| 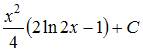
| ||
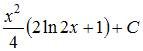
| |||
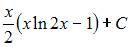
| |||
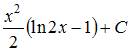
|
Решение:
Чтобы определить множество первообразных, вычислим неопределенный интеграл от этой функции методом интегрирования по частям по формуле 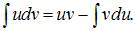 Тогда
Тогда
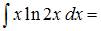
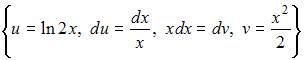
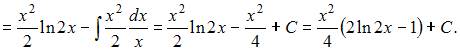
 ЗАДАНИЕ N 3 отправить сообщение разработчикам
ЗАДАНИЕ N 3 отправить сообщение разработчикам
Тема: Непрерывность функции, точки разрыва
Для функции 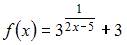 точка
точка 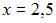 является точкой …
является точкой …

| разрыва второго рода | ||
| разрыва первого рода | |||
| непрерывности | |||
| устранимого разрыва |
Решение:
Вычислим односторонние пределы функции 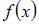 в точке
в точке 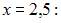
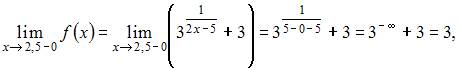
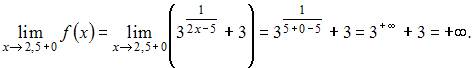
Так как один из односторонних пределов в точке 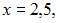 а именно
а именно 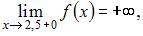 то точка
то точка 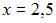 является точкой разрыва второго рода.
является точкой разрыва второго рода.
 ЗАДАНИЕ N 4 отправить сообщение разработчикам
ЗАДАНИЕ N 4 отправить сообщение разработчикам
Тема: Приложения определенного интеграла
Длина дуги кривой 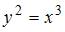 от точки
от точки 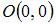 до точки
до точки 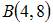 равна …
равна …

| 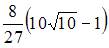
| ||
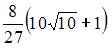
| |||
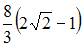
| |||
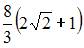
|
 ЗАДАНИЕ N 5 отправить сообщение разработчикам
ЗАДАНИЕ N 5 отправить сообщение разработчикам
Тема: Интерполирование функций: интерполяционные полиномы Лагранжа
Функция 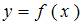 представлена таблицей
представлена таблицей
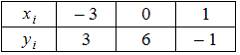
Тогда значение 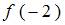 , вычисленное с помощью интерполяционного многочлена Лагранжа, равно …
, вычисленное с помощью интерполяционного многочлена Лагранжа, равно …

| 8 | ||
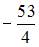
| |||
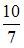
| |||
| – 6 |
 ЗАДАНИЕ N 6 отправить сообщение разработчикам
ЗАДАНИЕ N 6 отправить сообщение разработчикам
Тема: Численные методы решения дифференциальных уравнений и систем
Методом Эйлера с шагом 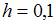 решается задача Коши для системы дифференциальных уравнений
решается задача Коши для системы дифференциальных уравнений 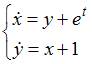 с начальными условиями
с начальными условиями 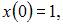
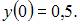 Тогда значения искомых функций
Тогда значения искомых функций 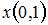 и
и 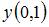 равны …
равны …

| 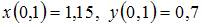
| ||
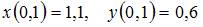
| |||
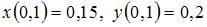
| |||
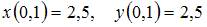
|
Решение:
Алгоритм Эйлера решения задачи Коши для системы дифференциальных уравнений:
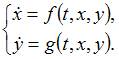
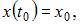
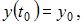
реализуется по формулам:
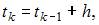
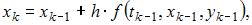
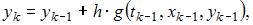
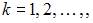
где h – шаг метода, 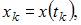
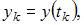 а
а 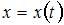 и
и 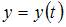 – искомые функции задачи Коши.
– искомые функции задачи Коши.
В рассматриваемой задаче требуется выполнить только один шаг метода Эйлера.
В нашем случае 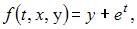
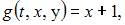
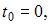
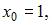
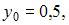
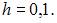
Тогда
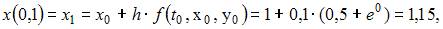
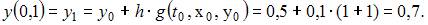
 ЗАДАНИЕ N 7 отправить сообщение разработчикам
ЗАДАНИЕ N 7 отправить сообщение разработчикам
Тема: Численное дифференцирование и интегрирование
Значение определенного интеграла 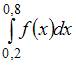 по формуле прямоугольников можно приближенно найти как …
по формуле прямоугольников можно приближенно найти как …

| 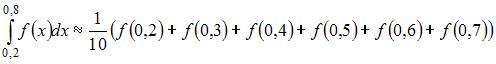
| ||
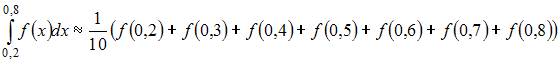
| |||
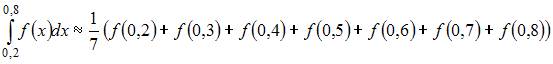
| |||
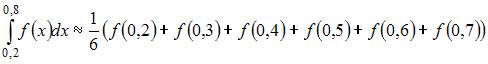
|
Решение:
Воспользуемся, например, формулой «левых» прямоугольников приближенного вычисления определенного интеграла: 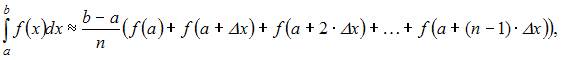
где 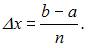 Пусть
Пусть 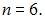 Тогда
Тогда 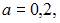
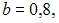
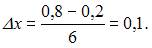 Следовательно,
Следовательно, 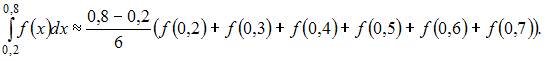
 ЗАДАНИЕ N 8 отправить сообщение разработчикам
ЗАДАНИЕ N 8 отправить сообщение разработчикам
Тема: Умножение матриц
Умножение матрицы A на матрицу B возможно, если эти матрицы имеют вид …

| 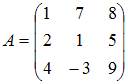 и и 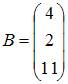
| ||
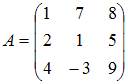 и и 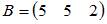
| |||
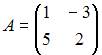 и и 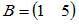
| |||
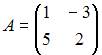 и и 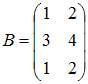
|
 ЗАДАНИЕ N 9 отправить сообщение разработчикам
ЗАДАНИЕ N 9 отправить сообщение разработчикам
Тема: Базис и размерность линейного пространства
Линейно зависимыми будут вектора …

| 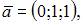 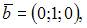 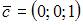
| ||
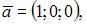 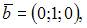 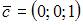
| |||
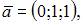 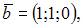 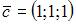
| |||
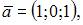 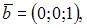 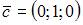
|
 ЗАДАНИЕ N 10 отправить сообщение разработчикам
ЗАДАНИЕ N 10 отправить сообщение разработчикам
Тема: Системы линейных уравнений
Система 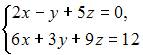 будет …
будет …

| совместной и неопределенной | ||
| несовместной и неопределенной | |||
| совместной и определенной | |||
| несовместной и определенной |
Решение:
По методу Гаусса приведем матрицу системы с помощью элементарных преобразований строк к трапецеидальной или треугольной форме. Запишем расширенную матрицу системы и преобразуем ее:
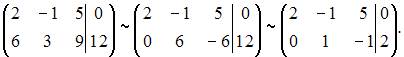 Значит, ранг расширенной матрицы равен рангу основной матрицы и система будет совместной. Так как количество переменных больше ранга матрицы, система имеет бесконечное число решений, а значит, является неопределенной.
Значит, ранг расширенной матрицы равен рангу основной матрицы и система будет совместной. Так как количество переменных больше ранга матрицы, система имеет бесконечное число решений, а значит, является неопределенной.
 ЗАДАНИЕ N 11 отправить сообщение разработчикам
ЗАДАНИЕ N 11 отправить сообщение разработчикам
Тема: Вычисление определителей
Определитель не равный нулю может иметь вид …

| 
| ||

| |||

| |||

|
 ЗАДАНИЕ N 12 отправить сообщение разработчикам
ЗАДАНИЕ N 12 отправить сообщение разработчикам
Тема: Дифференцирование функции комплексного переменного
Значение производной функции 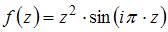 в точке
в точке 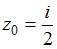 равно …
равно …

| 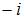
| ||
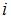
| |||
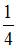
| |||
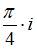
|
 ЗАДАНИЕ N 13 отправить сообщение разработчикам
ЗАДАНИЕ N 13 отправить сообщение разработчикам
Тема: Комплексные числа и их представление
Комплексное число задано в показательной форме 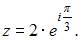 Тогда тригонометрическая форма записи сопряженного к нему числа
Тогда тригонометрическая форма записи сопряженного к нему числа 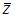 имеет вид …
имеет вид …

| 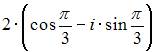
| ||
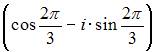
| |||
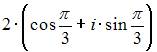
| |||
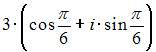
|
Решение:
Показательная форма комплексного числа имеет вид: 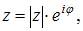
а тригонометрическая – 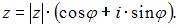 Так как
Так как 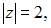
а главное значение аргумента 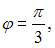 то
то 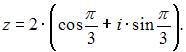 Если
Если 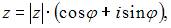 то
то 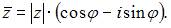 В нашем случае
В нашем случае 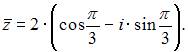
 ЗАДАНИЕ N 14 отправить сообщение разработчикам
ЗАДАНИЕ N 14 отправить сообщение разработчикам
Тема: Системы линейных уравнений с комплексными коэффициентами
Решение системы уравнений 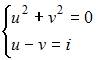 имеет вид …
имеет вид …

| 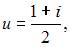 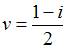
| ||
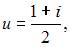 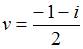
| |||
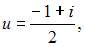 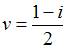
| |||
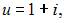 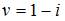
|
Решение:
Выразим 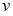 из второго уравнения
из второго уравнения 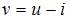 и подставим в первое уравнение системы
и подставим в первое уравнение системы 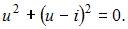 Получим квадратное уравнение
Получим квадратное уравнение 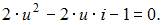 Его решения
Его решения 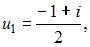
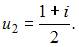 Соответствующие им значения переменной
Соответствующие им значения переменной 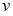 будут равны
будут равны 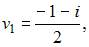
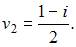 Таким образом, решения системы будут иметь вид:
Таким образом, решения системы будут иметь вид: 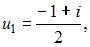
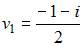 и
и 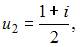
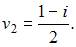
 ЗАДАНИЕ N 15 отправить сообщение разработчикам
ЗАДАНИЕ N 15 отправить сообщение разработчикам
Тема: Типы дифференциальных уравнений
Уравнение 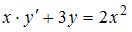 является …
является …

| линейным неоднородным дифференциальным уравнением первого порядка | ||
| однородным относительно x и y дифференциальным уравнением первого порядка | |||
| уравнением Бернулли | |||
| дифференциальным уравнением с разделяющимися переменными |
Решение:
Уравнение 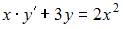 может быть сведено к уравнению вида
может быть сведено к уравнению вида 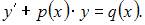 Действительно,
Действительно, 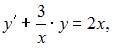 поэтому данное уравнение является дифференциальным линейным уравнением первого порядка.
поэтому данное уравнение является дифференциальным линейным уравнением первого порядка.
 ЗАДАНИЕ N 16 отправить сообщение разработчикам
ЗАДАНИЕ N 16 отправить сообщение разработчикам
Тема: Однородные дифференциальные уравнения
Общее решение дифференциального уравнения 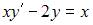 имеет вид …
имеет вид …

| 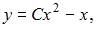 , где , где 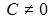
| ||
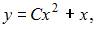 где где 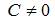
| |||
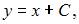 где где 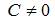
| |||
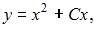 где где 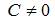
|
 ЗАДАНИЕ N 17 отправить сообщение разработчикам
ЗАДАНИЕ N 17 отправить сообщение разработчикам
Тема: Системы двух линейных дифференциальных уравнений с постоянными коэффициентами
Решение задачи Коши 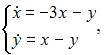
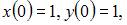 имеет вид …
имеет вид …

| 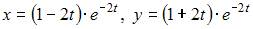
| ||
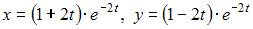
| |||
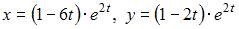
| |||
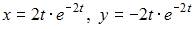
|
Решение:
Решим систему дифференциальных уравнений методом исключения.
Из второго уравнения находим 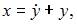 откуда
откуда 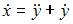 и после подстановки в первое уравнение системы получим линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами
и после подстановки в первое уравнение системы получим линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами 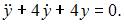 Характеристическое уравнение
Характеристическое уравнение 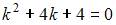 имеет кратные действительные корни:
имеет кратные действительные корни: 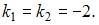 Таким корням соответствует общее решение однородного дифференциального уравнения
Таким корням соответствует общее решение однородного дифференциального уравнения 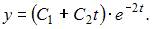
Дифференцируя полученное решение, находим 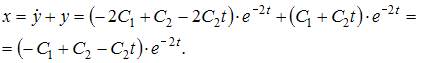
Тогда общее решение системы уравнений имеет вид 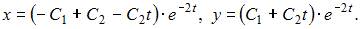
Найдём значения произвольных постоянных 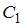 и
и 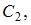 соответствующих исходной задаче Коши, подставляя начальные условия в общее решение. Получим систему уравнений
соответствующих исходной задаче Коши, подставляя начальные условия в общее решение. Получим систему уравнений 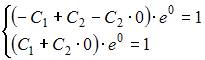 или
или 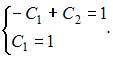
Решая эту систему, находим значения постоянных величин 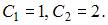
Поэтому решение задачи Коши имеет вид: 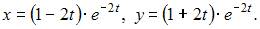
 ЗАДАНИЕ N 18 отправить сообщение разработчикам
ЗАДАНИЕ N 18 отправить сообщение разработчикам
Тема: Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
Частное решение 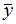 линейного неоднородного дифференциального уравнения второго порядка
линейного неоднородного дифференциального уравнения второго порядка 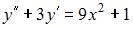 имеет вид …
имеет вид …

| 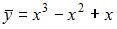
| ||
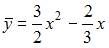
| |||
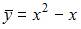
| |||
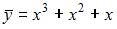
|
Решение:
Общее решение этого уравнения можно записать в виде 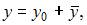 где функция
где функция 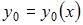 – общее решение однородного уравнения
– общее решение однородного уравнения 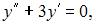 а функция
а функция 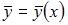 – некоторое частное решение исходного неоднородного уравнения.
– некоторое частное решение исходного неоднородного уравнения.
Для однородного уравнения составим характеристическое уравнение 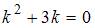 и найдем его корни:
и найдем его корни: 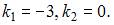 Тогда общее решение однородного уравнения будет иметь вид
Тогда общее решение однородного уравнения будет иметь вид 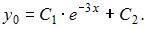
Поскольку правая часть исходного уравнения 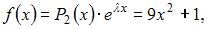 то имеем уравнение со специальной правой частью. Так как
то имеем уравнение со специальной правой частью. Так как 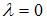 является простым корнем характеристического уравнения, то частное решение
является простым корнем характеристического уравнения, то частное решение 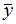 неоднородного уравнения будем искать в виде
неоднородного уравнения будем искать в виде 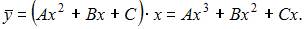
Подставим 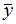 в исходное уравнение и найдем значения
в исходное уравнение и найдем значения 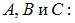
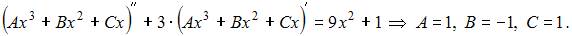
Следовательно, частное решение неоднородного уравнения 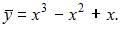
 ЗАДАНИЕ N 19 отправить сообщение разработчикам
ЗАДАНИЕ N 19 отправить сообщение разработчикам
Тема: Законы распределения вероятностей дискретных случайных величин
Среднее число заявок, поступающих на предприятие бытового обслуживания за 1 час равно трем. Тогда вероятность того, что за два часа поступит пять заявок можно вычислить как …

| 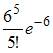
| ||
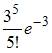
| |||
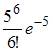
| |||
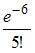
|
 ЗАДАНИЕ N 20 отправить сообщение разработчикам
ЗАДАНИЕ N 20 отправить сообщение разработчикам
Тема: Полная вероятность. Формулы Байеса
В первой урне 3 черных шара и 7 белых шаров. Во второй урне 4 белых шара и 6 черных шаров. Из наудачу взятой урны вынули один шар, который оказался черным. Тогда вероятность того, что этот шар вынули из второй урны, равна …

| 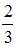
| ||
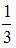
| |||
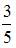
| |||
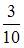
|








