1 2 . Представьте структурированные и неструктурированные данные и задачи. Какие из них чаще всего решаются средствами корпоративных ИС и почему?
Н ес т р ук т у риро в а нны е задачи имеют только качественное описание, основанное на суждениях ЛПР, количественные зависимости между основными характеристиками задачи не известны.
Структурированные задачи характеризуются существенными зависимостями, которые могут быть выражены количественно.
П о луструктурированные задачи занимают промежуточное положение и
являются "сочетающими количественные и качественные зависимости, причем малоизвестные и неопределенные стороны задачи имеют тенденцию доминировать"
1 3 . Что такое энтропия системы?
Принятой мерой неопределенности системы a является энтропия, обозначаемая H(a). При получении сообщения b энтропия системы - Нb(a). Как мы заметили, может быть, что Нb(a)< Н(a), Нb(a)> Н(a) и Нb(a)= Н(a) – все зависит от того, что за сообщение b получено. Интересно, что именно разность
Н(a)- Нb(a) оказывается важной характеристикой полученного сообщения b.
Этой важной характеристикой сообщения b о системе a является количество информации Ib(a), содержащееся в сообщении b о системе a:
Ib(a)= Н (a)- Нb(a)
Понятно, что Ib(a) может быть положительной – тогда сообщение уменьшает неопределенность, отрицательной – когда неопределенность растет и нулевой, когда сообщение не несет информации, полезной для принятия решения. В последнем случае
Н (a)= Нb(a):
т.е. неопределенность системы по получении сообщения b не изменилась и количество информации в b равно нулю.
Другим крайним случаем является ситуация, когда сообщение b полностью снимает неопределенность и Нb(a) = 0. В этом случае сообщение b содержит полную информацию о системе a и Ib(a)= Н (a).
Теперь для определения количества информации нам надо понять, как оценивать энтропию системы. В общем случае, энтропия системы, имеющей k возможных состояний, H(a), согласно формуле Шеннона, равна:
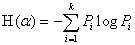 ,
,
где Pi – вероятность того, что система находится в i-м состоянии.
1 4 . Что такое количество информации по К.Шеннону?
В общем случае, энтропия системы, имеющей k возможных состояний, H(a), согласно формуле
Шеннона, равна: