Уравнения движения жидкости
Уравнения гидродинамики являются следствием фундаментальных законов сохранения массы, импульса и энергии.
Уравнение неразрывности
Составим материальный баланс неразрывного (сплошного) течения жидкости.
Рассмотрим в области течения произвольный объём V, ограниченный поверхностью S (Рис.2).
Рис.2. К выводу уравнения
неразрывности
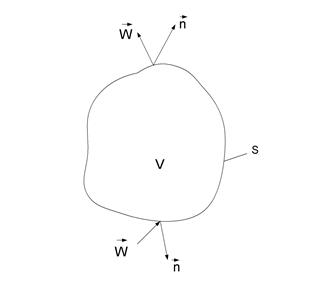В каждой точке этой поверхности проведём единичную нормаль 
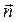. Будем считать, что источники массы внутри объёма V отсутствуют. Объёмный поток жидкости (расход) входящий в рассматриваемую область из жидкости, примыкающей к данному объёму, т.е. приток жидкости снаружи:
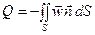(11)
Знак (-) в уравнении делает входящие потоки положительными.
Массовый поток найдём, умножив подинтегральное выражение на плотность
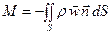M = [кг/с] (12)
Произведение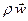 
называют массовой скоростью или плотностью массового потока.
Интеграл поверхности по формуле Остроградского-Гаусса преобразуем в интеграл по объёму
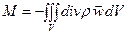(13)
Найдём то же изменение массы жидкости в единицу времени, рассматривая объём V изнутри
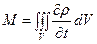
Приравнивая потоки, полученные определением притока массы снаружи и изнутри объёма V получим
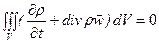(14)
Поскольку для произвольного объёма подинтегральная функция должна обращаться в нуль, получим уравнение неразрывности (сплошности)
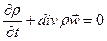(15)
Уравнение неразрывности является законом сохранения массы в дифференциальной форме. Для стационарного движения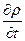 
=0, поэтому уравнение (15) принимает вид
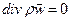(16)
Если жидкость несжимаема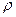 
= с onst, следовательно
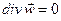(17)
Запишем это уравнение для компонентов скорости
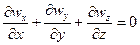(17а)
Записав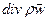 
в развёрнутой форме, из уравнения (15) получаем
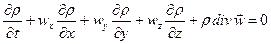
Это уравнение можно записать в следующем виде
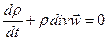(18)
где 
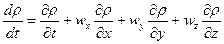(19)
Величина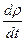 
называется индивидуальной (т.е. взятой для конкретной жидкой частицы) или субстанциональной производной.
Раскроем физический смысл индивидуальной производной.
Поскольку по методу Эйлера мы следим за изменением любой гидромеханической величины при прохождении жидкой частицы за время dt расстояний dx , dy , dz , то полный дифференциал плотности равен
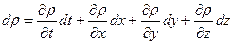, (20)
следовательно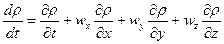
где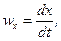 
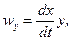
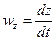
Первое слагаемое уравнения (20) означает изменение плотности в данной фиксированной (неподвижной) точке пространства в течение времени dt , а остальные слагаемые дают изменение 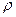за счёт перемещения частицы на расстояния dx , dy , dz.
Индивидуальная производная в форме уравнения (19) может быть записана для любой скалярной или векторной величины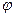 
(плотности, давления, скорости):
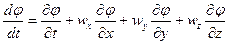(21)
Частную производную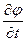 
также называют местной производной (т.е. для некоторой неподвижной в пространстве точки).
Из уравнения (21) можно также заключить, что - для нестационарного процесса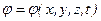 
, - для стационарного ( 
) 
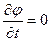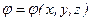
Получаем уравнение неразрывности в интегральной форме для стационарного течения жидкости.
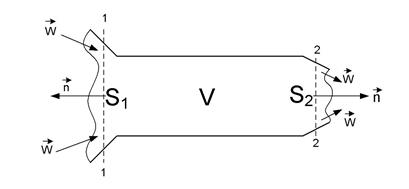Рассмотрим стационарное неразрывное течение жидкости в канале произвольной формы с непроницаемыми стенками (Рис.3).
Рис.3. К выводу уравнения неразрывности в интегральном виде
Запишем уравнения материального баланса (ур. 12-14) при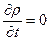 
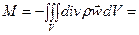
, для части канала, ограниченной плоскими сечениями 1 и 2 с поверхностями S 1 и S 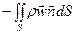2
(22)
Поскольку стенки непроницаемые, имеем равенство
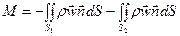(23)
Найдём положительные величины средней массовой скорости для сечений 1 и 2
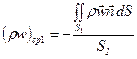
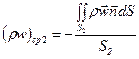(24)
Из уравнений (23) и (24) получим уравнение неразрывности в интегральной форме
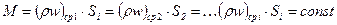(25)
В случае, когда плотность не меняется по сечению, имеем
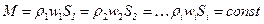(26)
где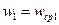 
, 
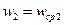и т.д.
Для несжимаемой жидкости
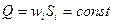(27)
Уравнения (25-27) служат для определения скоростей жидкости и площадей сечений каналов.