Силы, действующие на жидкость
Действующие на жидкие частицы силы подразделяются на внутренние и внешние.
К внутренним относятся силы взаимодействия между жидкими частицами внутри рассматриваемого объёма.
К внешним относятся силы, действующие на жидкость со стороны других тел (в том числе той же жидкости) окружающих этот объём жидкости или силы физических полей.
Внешние силы подразделяются также на два класса: объёмные (или массовые) и поверхностные.
Объёмные силы являются дальнодействующими, как например сила тяжести.
Они действуют на каждую жидкую частицу, причём в пределах этой частицы их можно считать постоянными. Объёмная сила пропорциональна величине объёма жидкой частицы.
Поверхностные силы действуют на поверхности, ограничивающие рассматриваемый объём жидкости.
ОСНОВНЫЕ ГИДРОМЕХАНИЧЕСКИЕ ВЕЛИЧИНЫ, ХАРАКТЕРИЗУЮЩИЕ ЖИДКОСТЬ
Выделим в покоящейся жидкости объём V, ограниченный поверхностью S.
Вектор сил, действующих на элемент поверхности dS,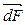 
будет расположен нормально к этой поверхности, так как покоящаяся жидкость не выдерживает касательных сил, т.е. 
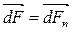( Рис.1)
 |
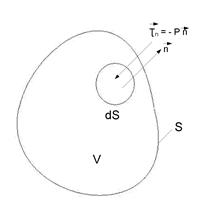Рис.1. К определению нормального напряжения
Проведём к поверхности dS внешнюю единичную нормаль (направленную из объёма V)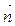 
. Сила 
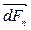будет всегда сжимающей, т.к. реальные технические жидкости практически не способны сопротивляться растягивающим усилиям без разрывов, т.е. без потери сплошности.
Определяем величину нормального напряжения:
 |
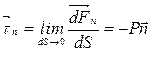(1)
где: Р - гидротехническое давление, являющееся модулем нормального напряжения.
Р= [ H/м2] = [ Па]
Основным свойством гидростатического давления является то, что его величина не зависит от ориентации площадки, на которую действует напряжение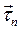 
.
Поскольку в двигающейся идеальной (невязкой) жидкости отсутствуют касательные напряжения и, соответственно, действуют только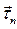 
, давление в такой жидкости идентично гидростатическому.
В движущейся реальной жидкости, за счёт вязкости присутствуют касательные напряжения, поэтому величина давления зависит от ориентации площадки действия. Но, для упрощения задачи, в реальной жидкости величину давления осредняют по различным направлениям и, таким образом, условно считают, что величина давления также не зависит от ориентировки площадки действия.
В этом случае величину Р называют гидродинамическим давлением.
Важнейшей величиной, характеризующей движение жидкости, является скорость физически бесконечно малого объёма (скорость в точке). Для её определения рассмотрим объём V, имеющий массу m и импульс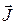 
.
Средней по объёму скоростью будет отношение имульса к массе:
 |
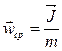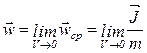Скоростью в точке будем называть следующий предел
(2)
В гидромеханике также широко используются средняя скорость по выбранной поверхности S, чаще всего по поперечному сечению потока
 |
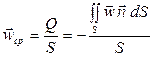(2а)
где: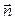 
– единичная внешняя нормаль к поверхности S
Q- объёмный поток жидкости (расход), входящей в сечение S, м3/с
Знак (-) означает, что входящий поток положительный.
В технических расчётах редко используют скорости в точке, там почти всегда оперируют средними скоростями, поэтому для удобства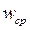 
обозначают 
( 
)
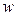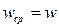Аналогично скорости определим плотность жидкости в точке
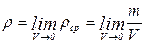(3)
Важной величиной, характеризующей движущуюся жидкость, является вязкость (динамическая вязкость), определяющая величину касательных напряжений. Экспериментально установлено, что скорость частиц жидкости, соприкасающихся с твёрдым телом, совпадает со скоростью этого тела (условие прилипания). Таким образом, например, скорость жидкости на поверхности неподвижной пластины равна нулю.
Рассмотрим пример движения жидкости между двумя параллельными пластинами площадью S, одна из которых (верхняя) движется с постоянной скоростью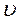 
, а другая неподвижна. Расстояние между пластинами h ( Рис 1а)
 |
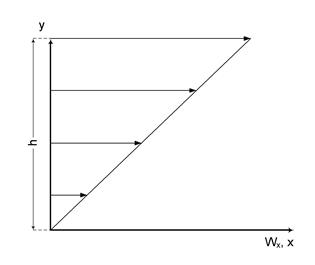Рис.1а. Профиль скорости между двумя параллельными пластинами, одна из которых движется.
При небольших значениях скорости движения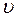 
, частицы жидкости, увлеченные верхней пластиной, будут двигаться слоями параллельно друг другу на всём протяжении расстояния h. В дальнейшем такой тип движения будет называться ламинарным.
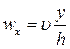Из такого опыта установлено, что скорость жидкости по оси x зависит линейно от расстояния y:
Также установлено, что для движения к верхней пластине необходимо приложить силу Т, направленную вдоль пластины, величина которой пропорциональна скорости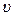 
и площади пластины S и обратно пропорциональна расстоянию h
 |
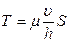Из результатов этого опыта найдём величину касательного напряжения
 |
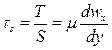Если координата y направлена в сторону уменьшения скорости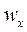 
, получим
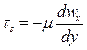(4)
где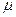 
- вязкость (динамическая вязкость).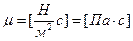 
В гидромеханике используется также кинематическая вязкость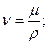 
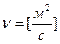
Уравнение (4) является формулировкой закона внутреннего трения Ньютона.
Вязкость жидкостей и газов определяется их природой, температурой и давлением.