Эффективная масса электронов в кристалле

Дата: 2025-06-02; Просмотры: 8
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

Уравнение движения электрона, записанное в виде (5.41), показывает, что величина 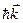по отношению к внешним силам ведет себя как импульс электрона.

Ускорение электрона под действием приложенного внешнего поля равно

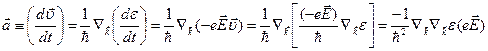. (5.44)

Таким образом, ускорение имеет компоненты

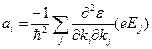. (5.45)

Сравнивая выражения (5.44) и (5.45) с уравнениями движения замечаем, что тензорная величина 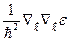имеет размерность (масса) 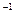. Поэтому величину

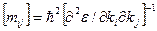(5.46)

называют тензором эффективной массы для электрона, находящегося в периодическом поле.

Для идеально простого изотропного твердого тела все недиагональные компоненты тензора эффективной массы обращаются в нуль, а три диагональные компоненты, допускаемые видом периодического потенциала, одинаковы. В таком идеальном твердом теле электрон имеет скалярную эффективную массу

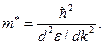(5.47)

Когда зависимость энергии от волнового вектора квадратична, то можно утверждать, что электроны обладают не зависящей от энергии эффективной массой, поскольку

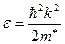. (5.48)

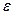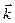В широком энергетическом интервале зависимость от энергия отклоняется от простого вида (5.48). Такое отклонение зависимости 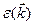от квадратичной часто описывают как зависимость эффективной массы от энергии. Эффективную массу следует рассматривать как удобный способ описания многих сложных явлений в твердом теле.

В качестве примера укажем, что в твердом теле с сильно анизотропной кристаллической структурой тензор эффективной массы может иметь положительные компоненты для одних направлений и отрицательные – для других.

Для любого периодического потенциала в зоне Бриллюэна найдутся точки, в которых уравнение Шредингера дает наименьшее возможное значение энергии электрона.

Пусть энергия электрона минимальна при 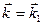(и в соответствующем числе точек, эквивалентных 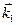). Тогда все три главные компоненты тензора массы 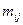, как правило, положительны в окрестности точки 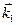. Более того, для энергий, отличающихся от 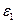на доли электронвольта, эффективная масса обычно практически не зависит от энергии:

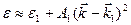. (5.49)

Однако в этом выражении 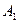обычно зависит от направления вектора ( 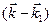. Таким образом, для электронов, расположенных у дна зоны разрешенных энергий, энергию можно записать в виде

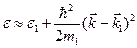, (5.50)

где 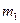- эффективная масса для данного направления в 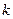-пространстве, отсчитываемого от зонного минимума.

В тех частях зоны Бриллюэна, где энергия электрона достигает максимума, по-видимому, все три компоненты 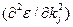отрицательны, так что следует записать

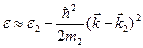. (5.51)

Электрон, принадлежащий к такой группе энергетических состояний, реагирует на поле так, как если бы он обладал отрицательной массой. Точка реального пространства, в которой находится незаполненное состояние возле потолка зоны, перемещаясь по кристаллу, ведет себя как частица, которую обычно называют положительной дыркой. Дырка имеет положительный заряд (по сравнению с зарядом заполненного состояния) и положительную массу .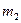

Обратим внимание на то, что массы 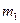и 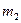в формулах (5.50) и (5.51) не равны друг другу и ни одна из них не равна обычной массе электрона. Величины 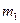и 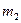отражают способность электрона у дна зоны или дырки у ее потолка реагировать на внешнее поле, действующее совместно с межатомным периодическим потенциалом.

Для промежуточных областей энергетического интервала внутри зоны, расположенных достаточно высоко по отношению к 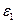и достаточно низко по отношению к 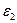тензор эффективной массы имеет более сложный вид.