Динамика движения электронов

Дата: 2025-06-02; Просмотры: 9

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Движение электрона описывается волновым пакетом, который движется по решетке в реальном пространстве с групповой скоростью 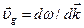. Рассмотрим сначала движение волнового пакета в одномерном кристалле при наличии внешнего электрического поля. Предположим, что волновой пакет состоит из волновых функций одной энергетической зоны с волновыми векторами, близкими к некоторому вектору 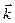. Частота, связанная с волновой функцией, отвечающей энергии 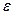, равна 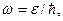и поэтому

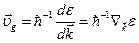. (5.37)

Влияние кристалла на движение электрона целиком заключается в дисперсионном законе 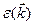. Элементарная работа 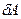, совершаемая полем Е над электроном за время 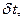равна

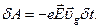(5.38)

Работа, совершаемая внешней силой 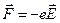, затрачивается на изменение энергии 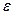электрона

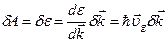; (5.39)

Сравнивая (5.38) с (5.39), получим:

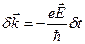, (5.40)

следовательно, уравнение движения запишется в виде

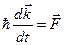. (5.41)

Это очень важный результат: в кристалле 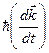равно внешней силе, действующей на электрон.

Будем полагать, что полученный результат сохраняется и в случае, если в качестве внешней силы взять силу Лорентца, действующую на электрон, движущийся в магнитном поле.

Уравнение движения электрона, движущегося с групповой скоростью 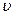в постоянном магнитном поле 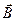, запишется в виде

(СГС) 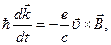(5.42)

(СИ) .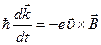

С учетом того, что 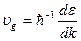= 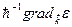получим

(СГС) 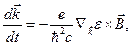(5.43)

(СИ) .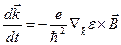

Из векторного произведения в (5.43) следует, что в магнитном поле электрон в 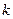-пространстве движется в направлении, перпендикулярном к направлению градиента энергии 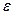, т.е. электрон движется по поверхности постоянной энергии. Движение в 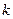-пространстве происходит в плоскости, перпендикулярной к направлению 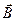, и орбита электрона определяется пересечением этой плоскости с поверхностью постоянной энергии.

В магнитном поле возможны три типа орбит (рис. 5.15).

Замкнутые орбиты на рис. 5.15, а и 5.15, б проходятся в противоположных направлениях, поскольку частицы противоположного знака в магнитном поле вращаются в противоположных направлениях. В связи с этим об одной из орбит говорят как характерной для электрона, а о другой - как характерной для дырки.

По орбитам, характерным для дырок, электроны движутся в магнитном поле так, как если бы они обладали положительным зарядом. Поэтому дырки приводят к положительным значениям коэффициента Холла. В случае, изображенном на рис. 5.15, в, орбита не замкнута. Частица, достигнув точки А на границе зоны, автоматически оказывается в точке В (перебрасывается) на противоположную границу. Точка В эквивалентна точке 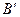, поскольку расстояние между ними составляет как раз вектор обратной решетки. Такая орбита называется открытой орбитой. Открытые орбиты играют важную в явлении магнетосопротивления.

Дырки

Существование дырок — одна из наиболее интересных осо­бенностей зонной теории твердых тел. Эта особенность не толь­ко интересна, но и практически важна, потому что действие транзисторов непосредственно связано с сосуществованием в по­лупроводниковых кристаллах электронов и дырок.

Незанятые электронами (вакантные) состояния в разрешен­ной зоне обычно называют дырочными состояниями (дыроч­ными орбиталями). Наиболее нагляден случай, когда вблизи потолка разрешенной энергетической зоны имеется одно вакант­ное состояние (а все остальные заняты); такая ситуация возни­кает чаще в полупроводниках, чем в металлах. Понятие дыроч­ ной орбиты также относится к числу хорошо определенных, даже если в зоне число вакантных состояний (орбиталей) превышает число занятых, хотя топологическая природа той или иной конк­ретной орбиты может зависеть от направления внешнего маг­нитного поля. Свойства самих дырок устанавливаются из более сложных соображений.

Эксперименты по циклотронному резонансу в полупроводни­ках при использовании циркулярно поляризованного электро­магнитного излучения позволили установить (см. гл. 11), что дырки и электроны вращаются в магнитном поле в противопо­ложных направлениях, как и следовало ожидать для зарядов противоположного знака. Кроме того, было установлено, что при одном направлении круговой поляризации электромагнитные волны поглощаются электронами, а при обратном—дырками.

Рассмотрим перемещение дырки во внешнем электрическом поле, используя схему, приведенную на рис. 10.11. В исходном состоянии зона заполнена целиком, за исключением одного со­стояния в вершине зоны, которое обозначено буквой F . Затем в положительном направлении оси х наложено электрическое поле Е_х.

Уравнение, описывающее движение электронов в зоне, имеет

обычный вид

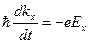(10.8)

и утверждает, что у каждого электрона 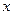-компонента волно­вого вектора k_x изменит свою величину в один и тот же момент времени. Из схемы на рис. 10.11 видно, что приращение 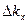бу­дет отрицательным. Вакантное состояние, первоначально находившееся и точке 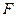, сначала сместится на уровень 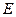, а затем на уровень D . Это значит, что при перемещении электронов дырка будет перемещаться в направлении —k_x .

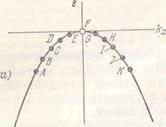
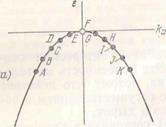
Рис. 10.11. а) В момент 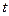= Q все со­стояния заняты, за исключением F в вер­шине зоны. В точке F скорость v_x равна нулю, поскольку d 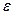/ dk_x = 0. б) Элек­трическое поле 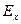приложено вдоль по­ложительного направления оси х. Сила, действующая на электрон со стороны поля, приложена в направлении — 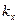, а электроны последовательно перемещают­ся по кривой, сдвигая дырку в положе­ние Е.

Суммарный волновой вектор электронов в заполненной энер­гетической зоне равен нулю:

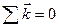. (10,9)

Этот результат следует из геометрической симметрии зоны Бриллюэна. Каждому из основных типов решетки (см. гл. I) свойственна инвариантность при операции инверсии: 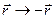от­носительно любой точки решетки. Из геометрического опреде­ления этой операции следует, что и зоны Бриллюэна для каж­дой такой решетки обладают инверсионной симметрией. Итак, если в энергетической зоне заполняются все пары состояний k , то неизбежно заполняются и все пары —k и, следовательно, полный волновой вектор равен нулю.

Даже для заполненной зоны каждый электрон изменяет свою величину k с быстротой, определяемой, как было установлено выше, уравнением 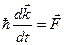. Электроны, достигшие границы зоны, не блокируются границей, а «перебрасываются» на противоположную границу, чтобы «начать жизнь снова».

Если зона целиком заполнена, за исключением одного состоя­ния, скажем в точке 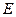(см. рис, 10.11, б), говорят, что состояние 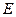является дыркой. Физические свойства дырки вытекают из факта заполненности электронами всех остальных состояний зоны. Это утверждение есть ключ к пониманию понятия дырки. Прежде всего используем это утверждение для введения волнового вектора дырки. Если электрон удален in состояния, характеризуемого волновым вектором k_e , то полный волновой вектор системы станет равным —k_e и дырке следует приписать волновой вектор .

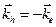Это несколько удивительно: ведь электрон удаляется из состоя­ния 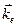, а образовавшуюся дырку считают локализованной именно в состоянии k_e , как мы и изображали на схеме рис. 10.11.

Однако истинный волновой вектор дырки равен —k_e , который соответствует точке G , когда дырка — в точке Е. Именно такой волновой вектор —k_e фигурирует в правилах отбора, где участвует поглощение фотонов (рис. 10.12).

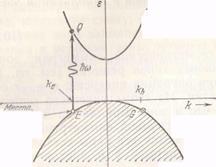
Рис. 10.12. После поглоще­ния фотона (с энергией 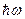и пренебрежимо малым вол­новым вектором) электрон покидает состояние Е в за­полненной валентной зоне и переходит в состояние Q в зоне проводимости. Если волновой вектор электрона в состоянии Е был равен 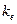, то в состоянии Q он оста­ется тем же. Полный волно­вой вектор валентной зоны после поглощения фотона равен — 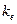, и именно такой волновой вектор мы должны приписать дырке, если мы рассматриваем валентную зону как зону, занятую одной дыркой. Таким образом, 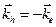. Волновой вектор дырки такой же, как волновой вектор электрона, который остается в состоянии G. Для системы и целом полный волновой вектор после поглощения фотона ра­вен 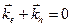, так что полный волновой вектор остается неизменным при поглощении фотона и образовании свободного электрона и свободной дырки.

Уравнение движения электрона в кристалле имеет вид 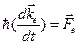, где F_e — сила, действующая на электрон. По­скольку 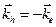, то

; .

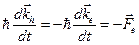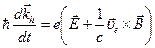Это уравнение движения положительного заряда в электрическом поле; оно описывает также движение положительного заряда в магнитном поле, при условии, что 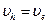. Доказатель­ство этого равенства дается ниже. Причина того, что знак про­изводной 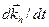противоположен знаку 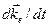, ясна из рис. 10.11: в к-пространстве вакантное состояние перемещается в последо­вательности Е — >• D — >• С —> . . . , как если бы оно было положи-тельным электроном, однако в действительности перемещаются электроны Е, D , . . . , не имеющие парных справа, т. е. соответствующие последовательности G —H—I ...

Здесь 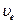— скорость «отсутствующего» электрона. Скорость
же дырки 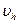(групповая скорость) определяется из следующих
соображений. Если какой-то электрон покидает состояние Е (см.
рис. 10.11,б), то суммарный электрический ток j, создаваемый
переносом зарядов в зоне, обусловлен реальным движением парного ему электрона и состоянии G:

.

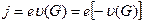Этот ток можно трактовать как следствие движения положительного заряда е со скоростью -v(G). Поскольку скорость -v ( G ) равна скорости v ( E ) в состоянии Е, т. е. в состоянии, из которого переместился электрон, то тот же ток можно запи­сать в виде

j= ev ( E ). (10.14)

Итак, мы имеем: v ( E )=-v ( G ), поскольку производная d 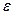/ dk имеет противоположные по знаку значения в точках Е и G. Ток можно описывать, приписывая дырке положительный за­ряд и скорость, равную скорости электрона, создающего ва­кантное состояние.

Пусть электрон покидает состояние, характеризуемое вол­новым вектором k_e . Если v_e — скорость электрона, которую он имел в состоянии k_e , то

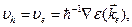(10.15)

где через 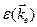обозначена энергия электрона в состоянии k_e . Для удобства мы можем положить равной нулю энергию, соответствующую верхнему краю заполненной (или почти цели­ком заполненной) зоны; тогда 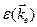будет отрицательной во всех точках зоны. Дырка, которая возникает, когда электрон покидает состояние 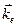, будет иметь положительную энергию 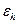, причем

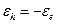. (10.16)

Энергия дырки противоположна по знаку энергии покинувшего соответствующее состояние электрона; процесс удаления
электрона из состояния с низкой энергией требует большей работы, чем из состояния с высокой энергией (внутри энергетической зоны). В случае симметричной зоны из (10.15) и (10.17)
имеем:

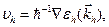(10.18)

где оператор градиента относится к k_h . Из (10.12) и (10.15) по­лучим уравнение движения для дырки:

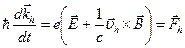, (10.19)

где 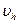можно определить из (10.15) или (10.18). Результат (10.19) есть уравнение движения для положительного заряда, которое сразу дает объяснение отличию в знаке постоянной Холла для дырок по сравнению с электронами или для полупро­водников р-типа по сравнению с полупроводниками n-типа.

Эффективная масса дырки (см. следующий раздел) отрица­тельна, т. е. знак ее противоположен знаку массы электрона, уход которого и был причиной возникновения этой дырки. Эф­фективная масса электрона в состоянии k_e , в котором он имел скорость v_e , определяется из уравнения движения, записанного в форме второго закона Ньютона, а именно m_e ( dv_e / dt )= - eE . Эффективная масса дырки определяется уравнением движения той же формы, но с положительным зарядом е, т. е. 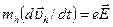. Согласно (10.15) v_e = v_h , и,- следовательно, 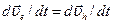. Сравнивая между собой уравнения движения для электрона и для дырки, сразу получаем:

.

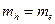Имеется различие между поведением одиночной дырки вблизи потолка в остальном целиком заполненной зоны и одиночного элек­трона вблизи потолка пустой (в остальном) зоны. Одиночный электрон имеет отрицательный заряд, и, в соответствии с соображениями, приведенными в следующем разделе, его эффективная масса вблизи потолка зоны отрицатель­на. Дырка в аналогичном положении в зоне ведет себя так, как если бы она обладала положительным зарядом и положительной массой. Таким образом, отношение заряда к массе одно и то же как для одиночного электрона, так и для соответствующей одиночной дырки. Отсюда следует, что как электрон, так и дырка в электрическом поле будут приобретать ускорение в одном на­правлении, но в случае дырки поле будет затрачивать работу, тогда как в случае электрона - наоборот: электрон будет отдавать энергию, а поле - приобретать. В статическом магнитном поле направление вращения электрона и дырки будет одно и то же.

В таких эффектах, как электропроводность, которые зависят от отношения (заряд)²/масса, вклады электронов и дырок следует учитывать по от­дельности. Проводимость, обусловленная дыркой, будет положительной ( 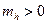), следствием чего будет поглощение энергии образцом в электриче­ском поле. Проводимость, обусловленная изолированным электроном в со­стоянии с отрицательной массой ( 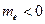), будет отрицательной¹), след­ствием чего будет генерация (а не поглощение) энергии образцом, помещен­ным в электрическом поле.

Состояние электрона с т_е < О является неустойчивым.

Заметим, что электроны, обладающие большими энергиями 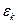, обнаружи­вают стремление перейти в состояния более низких энергий, что отвечает стремлению системы к тепловому равновесию, тогда как дырки с малыми энергиями 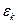, стремятся, так сказать, «всплыть» вверх - к уровням, отвечаю­щим большим энергиям.