Модель почти свободных электронов

Дата: 2025-06-02; Просмотры: 7
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

Зонная теория твердых тел

 

Первой удачной попыткой объяснения электрических и магнитных свойств твердых тел, в первую очередь металлов, была теория свободных электронов. Дальнейший этап в развитии электронной теории является зонная теория твердых тел. Эта модель позволяет понять, почему одни химические элементы хорошие проводники, другие изоляторы или полупроводники, электрические свойства которых резко зависят от температуры. Различие в сопротивлениях металлов ( 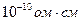) и диэлектриков ( 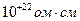) просто поразительно, поскольку ни одна физическая величина, характеризующая свойства твердых тел, такого разброса значений не имеет.

 

Энергетические уровни свободных атомов. Состояние электронов в атоме определяется 4 квантовыми числами: главным - 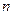, орбитальным - 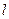, магнитным - 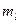и спиновым - 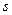. Для атома водорода и водородоподобных атомов 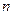определяет энергию атомов в стационарных состояниях

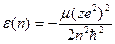(4.1)

и принимает значения .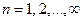

Орбитальное квантовое число 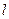определяет орбитальный момент количества движения электрона

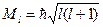(4.2)

и принимает значения .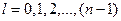

Магнитное квантовое число 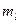определяет ориентацию орбитального момента количества движения относительно избранного направления магнитного поля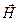

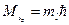(4.3)

и принимает значения .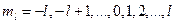

Спиновое квантовое число 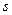определяет ориентацию собственного момента количества движения электрона относительно выделенного направления магнитного поля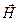

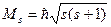(4.4)

и принимает значение 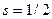. Проекция собственного момента количества движения электрон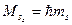а , а 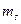принимает значения .

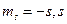Состояния 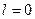называют 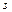-состояние, 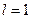- -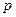состояние, 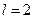- d-cостояние.

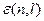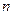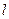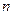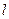В многоэлектронных атомах энергия зависит от и . Так как и принимают дискретные значения, то и 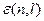принимает дискретные значения, разделенные областью запрещенных энергий.

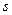-уровень не является вырожденным; 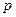-уровень трехкратно вырожден. При помещении атома в сильное внешнее поле вырождение снимается, каждый уровень расщепляется на 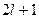уровней.

 

Обобществление электронов в кристалле. В твердых телах атомы оказываются в сильном поле соседних атомов. Чтобы проследить какое влияние поле оказывает на энергетические уровни, рассмотрим следующий идеализированный пример.

Расположим 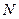атомов Na в виде пространственной решетки на расстояниях, когда их взаимодействием можно пренебречь. В этом случае атомы можно считать изолированными (рис. 4.1а)

 

Рис. 4.1а. Энергетические Рис. 4.1б. Энергетический спектр уровни изолированного атома. электронов в кристалле.

 

Уровни 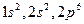- заполнены, а уровень 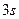- наполовину; уровни выше 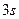- свободны. Потенциальный барьер 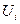для электронов на разных уровнях различен; 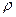- соответствует плотности вероятности обнаружения электрона на расстоянии 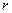от ядра.

Подвергнем решетку медленному однородному сжатию, не нарушая симметрии. На рис. 4.1б показано состояние при 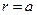, где 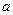- постоянная решетки. Результирующие потенциальные кривые проходят ниже нулевого уровня, а их толщина уменьшается. Для электронов 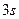- уровня высота барьера оказывается ниже первоначального положения уровня 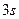в атоме Na. Поэтому валентные электроны этого уровня получают возможность практически беспрепятственно перемещаться от одного атома к другому. Об этом свидетельствует и характер электронных облаков. Из-за сближения атомов свободу перемещения получают и электроны на других уровнях. Перемещение происходит путем туннельного перехода их сквозь барьеры, отделяющие соседние атомы.

Энергетический спектр электронов в кристалле. Подобно тому, как основной задачей теории атома является описание состояний электронов в атоме и вычисление разрешенных уровней энергии, одна из основных задач теории твердого тела заключается в определении энергетического спектра электронов в кристалле. Каждый уровень в кристалле, состоящем из 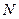атомов, повторяется 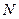раз, т.е. каждый уровень оказывается 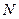-кратно вырожденным, образуя энергетическую зону.

Так уровень 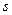дает зону 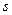, состоящую из 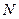подуровней и способную вместить 2 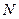электронов; уровень 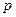дает зону 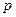, состоящую из 3 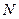подуровней, способную вместить 6 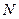электронов.

Наибольшее влияние поле решетки оказывает на внешние валентные электроны атома, поэтому энергетические зоны из энергетических уровней этих электронов наиболее широкие.

 

Модель почти свободных электронов

 

Зонная энергетическая структура кристалла может быть описана на основе модели почти свободных электронов. В этой модели учитывается действие на электроны слабого возмущающего поля периодического потенциала ионных остовов. Модель почти свободных электронов позволяет объяснить общие черты зонной структуры, так и тонкие детали формы наблюдаемых поверхностей Ферми.

Волновое уравнение для электрона в периодическом потенциале. Ионы в решетке образуют периодическую структуру. Поэтому рассмотрим задачу об электроне в потенциале 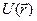, который имеет периодичность решетки Бравэ, лежащей в основе этой структуры

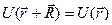. (4.5)

Так как характерный период потенциала ~ 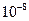см, т.е. совпадает с длиной волны де-Бройля электрона, то для описания движения электрона в периодическом потенциале воспользуемся квантовой механикой. Задача об электроне в твердом теле в принципе представляет собой многоэлетронную задачу, поскольку полный гамильтониан твердого тела содержит не только одноэлектронные потенциалы, описывающие взаимодействие электронов с атомными ядрами, но и парные потенциалы, описывающие взаимодействие между электронами. В приближении независимых электронов это взаимодействие учитывается с помощью эффективного одноэлектронного потенциала 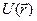. Какова бы не была форма этого потенциала он должен удовлетворять уравнению (4.5).

Итак, нам необходимо изучить те общие свойства одноэлектронного уравнения Шредингера

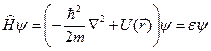, (4.6)

которые обусловлены периодичностью потенциала 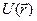. Независимые электроны, каждый из которых удовлетворяет уравнению (4.6), называются блоховскими.

Теорема Блоха. Собственные состояния 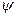одноэлектронного гамильтониана 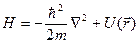, где 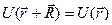при всех 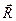из решетки Бравэ могут быть выбраны так, чтобы их волновые функции имели форму плоской волны, умноженной на функцию с периодичностью решетки Бравэ, т.е.

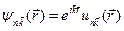, (4.7)

где

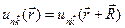(4.8)

для всех 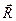из решетки Бравэ. Из (4.7) и (4.8) следует равенство

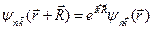. (4.9)

Доказательство. Определим для каждого вектора 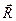решетки Бравэ оператор трансляции, под действием которого аргумент функции 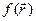сдвигается на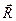

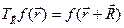. (4.10)

В силу периодичности гамильтониана имеем

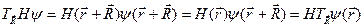. (4.11)

Поскольку уравнение (4.11) выполняется тождественно для любой функции 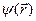, справедливо следующее операторное тождество

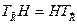. (4.12)

Результат двух последовательных трансляций не зависит от порядка их применения, поскольку для любой функции имеем

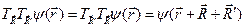, (4.13)

поэтому

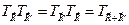. (4.14)

Таким образом гамильтониан H и операторы 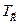для всех векторов 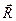решетки Бравэ образуют набор коммутирующих операторов. Из фундаментальной теоремы квантовой механики следует, что тогда собственные состояния оператора H можно выбрать так, чтобы они одновременно являлись собственными состояниями оператора :

,

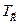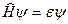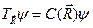. (4.15)

Собственные значения 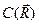оператора трансляции связаны между собой в силу условия (4.14)

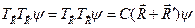. (4.16)

Следовательно, для собственных значений должно выполняться равенство

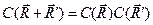. (4.17)

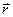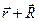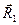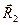Переход из точки в точку можно совершить либо непосредственно, либо путем двух последовательных трансляций на векторы и , удовлетворяющих условию 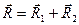. Волновую функцию 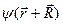в этих случаях можно представить либо как

,

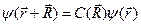либо как

.

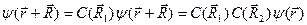Отсюда

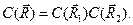(4.18)

Следовательно, логарифм коэффициента 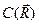является аддитивной функцией:

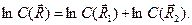
Сопоставляя это выражение с 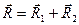, можно заключить, что

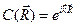. (4.19)

Итак, мы показали, что собственные состояния 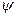гамильтониана H можно выбрать таким образом, что для каждого вектора 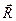решетки Бравэ выполняется равенство

.

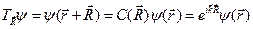Но это и есть теорема Блоха в формулировке (4.9). Полученному условию удовлетворяет также функция более общего вида:

.

 

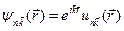Граничные условия Борна-Кармана. Налагая на волновые функции соответствующие граничные условия можно показать, что должен быть действительным и получить условия, которым должны удовлетворять разрешенные значения . Граничные условия выбираем так, чтобы они удовлетворяли условию макроскопической периодичности. Выберем ящик соразмерный элементарной ячейке соответствующей решетки Бравэ.

Обобщим граничные условия, записав их в форме

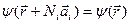, (4.20)

где 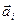- тройка основных векторов, а 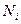- целые числа порядка 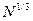, так что 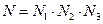- полное число элементарных ячеек в кристалле.

Применим к граничному условию теорему Блоха

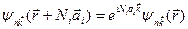, i = 1, 2, 3 (4.21)

с учетом (4.20)

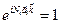, i = 1, 2, 3. (4.22)

Если 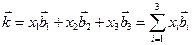, то

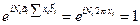. (4.23)

Следовательно, должно выполняться условие 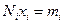- целое число. Поэтому разрешенный блоховский волновой вектор должен иметь следующий вид

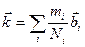. (4.24)

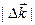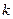Из (4.24) следует, что объем в - пространстве, приходящийся на одно разрешенное значение , равен объему маленького параллелепипеда с ребрами :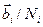

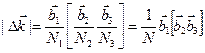, (4.25)

где 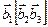- объем элементарной ячейки обратной решетки, поэтому число разрешенных волновых векторов, содержащихся в одной элементарной ячейке, равно числу ячеек в кристалле.

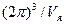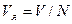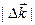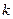Объем элементарной ячейки обратной решетки равен , где - объем элементарной ячейки прямой решетки. Таким образом, объем в - пространстве равен

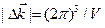. (4.26)

 

Волновое уравнение для электрона в периодическом потенциальном поле. Разложение периодических функций по плоским волнам. В дальнейшем для решения уравнения Шредингера в слабом периодическом потенциале нам потребуется использовать разложение периодических функций по плоским волнам.

Любую функцию, подчиняющуюся граничному условию Борна-Кармана, можно разложить по набору всех плоских волн, удовлетворяющих этому граничному условию

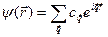. (4.27)

Потенциал 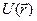имеет периодичность решетки, поэтому в его разложении по плоским волнам, будут входить только плоские волны с периодичностью решетки, поэтому их волновые векторы являются векторами обратной решетки

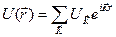, (4.28)

где суммирование ведется по всем векторам обратной решетки .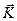

Фурье-коэффициенты 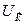связаны с 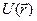соотношением

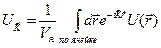. (4.29)

Поскольку потенциальную энергию всегда можно изменить на аддитивную постоянную величину, выберем эту величину так, чтобы пространственное среднее значение 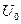потенциала, взятое по элементарной ячейке, обращалось в нуль:

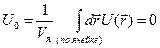. (4.30)

Заметим, поскольку 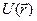действителен, то из (4.29) следует, что его фурье-компоненты удовлетворяют соотношению

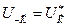. (4.31)

Пусть кристалл обладает центром инверсии, тогда при определенном выборе начала отсчета 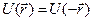; тогда 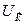действительная величина, и поэтому

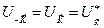. (4.32)

Теперь подставим разложения (4.27) и (4.28) в уравнение Шредингера (4.6). Слагаемое с кинетической энергией дает

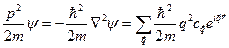. (4.33)

Слагаемое с потенциальной энергией может быть записано в форме

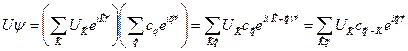. (4.34)

Заменим обозначения индексов суммирования 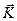и 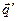в (4.34) на 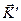и 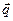; тогда уравнение Шредингера принимает вид

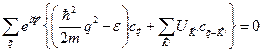. (4.35)

Так как плоские волны, удовлетворяющие условию Борна-Кармана, образуют ортогональный набор, коэффициент при каждом слагаемом в (4.35) должен быть равен нулю, поэтому для всех разрешенных волновых векторов 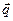получаем

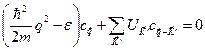. (4.36)

|Вставка. Ортогональность различных Фурье-компонент:

|

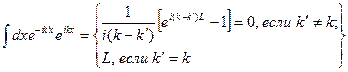
|Умножим обе части уравнения (4.35) на 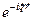и проинтегрируем - получим (4.36).

 

Удобно записать 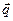в форм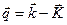е , где 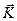- вектор обратной решетки, выбранный так, чтобы вектор лежал в первой зоне Бриллюэна. Уравнение (4.36) тогда имеет вид

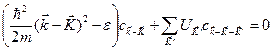, (4.37)

или, если сделать замену переменных ,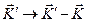

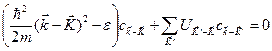. (4.38)

Подчеркнем, что (4.36) и (4.38) представляют всего лишь новую форму записи исходного уравнения (4.6) в импульсном пространстве, которая оказывается более простой из-за того, что в силу периодичности потенциала коэффициенты 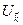отличны от нуля только для тех , которые являются векторами обратной решетки.

Уравнение (4.38) является самым важным уравнением зонной теории твердого тела.

При фиксированном из первой зоны Бриллюэна система уравнений (4.38) при любом значении вектора обратной решетки 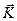связывают между собой только коэффициент Фурье 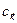компонент плоской волны какой-либо конкретной орбитали с бесконечным числом других коэффициентов Фурье 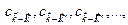у которых волновые векторы отличаются от на вектор обратной решетки для всех других плоских волн, которые входят в ряд Фурье этой орбитали.

Таким образом, получаем систему из бесконечного числа независимых уравнений одинаковой формы, вычитая из последовательно возрастающие векторы обратной решетки. Поскольку эта система из бесконечного числа уравнений, то будет существовать бесконечно много различных значений энергии для любого данного . Наиболее интересными для нас будут решения, отвечающие наинизшей энергии.

Эти соображения станут ясными, если выписать уравнения для конкретной задачи. Обозначим через 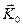наименьший из векторов обратной решетки 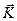. Предположим, что выражение для потенциальной энергии содержит лишь один член, т. е. одну компоненту Фурье 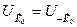, которую обозначим через 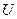. Тогда система (4.38) для фиксированного 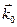будет содержать лишь три уравнения:

 

 

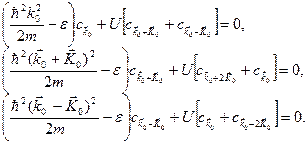
Видно, что второе и третье уравнения получаются из первого заменой 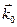на 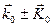. Коэффициенты 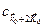и 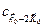становятся связанными между собой и следует выписать еще два уравнения с 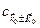и т.д. до бесконечности.

Следовательно, исходная задача распалась на 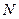независимых задач – для каждого разрешенного значения в первой зоне Бриллюэна. Каждая такая задача имеет решение, которое является суперпозицией плоских волн, содержащих только волновой вектор и волновые векторы, отличающиеся от на какой-либо вектор обратной решетки.

Используя полученные результаты, вернемся к разложению волновой функции (4.27). Видно, что волновой вектор 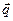принимает лишь значения 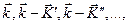а волновая функция имеет следующий вид

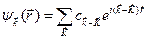. (4.39)

Если переписать это выражение как

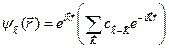, (4.40)

то видно, что функция имеет блоховскую форму (4.7) 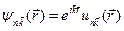, причем периодическая функция 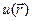дается выражением

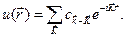(4.41)

При фиксированном существует бесконечно много решений системы уравнений (4.38). Для их перечисления используют номер зоны .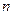

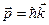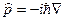Импульс электрона в кристалле. В модели свободных электронов импульс электрона . В блоховском случае волновой вектор не пропорционален импульсу электрона. Это следует из того, что гамильтониан в присутствии неоднородного потенциала не обладает полной трансляционной инвариантностью. Действительно, подействовав оператором импульса на 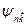, получим

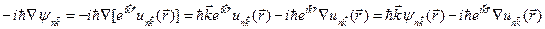. (4.42)

Это уравнение не имеет вида соnst 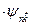, т.е. 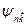не является собственным состоянием оператора импульса. Тем не менее, часто 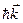служит естественным обобщением импульса на случай периодического потенциала. Чтобы подчеркнуть сходство и указать отличие 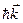от истинного импульса, эту величину называют квазиимпульсом электрона. Волновой вектор , входящий в теорему Блоха, можно всегда считать относящимся к первой зоне Бриллюэна. Это справедливо потому, что если вектор 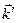не лежит в первой зоне Бриллюэна, то его можно представить в виде

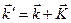, (4.43)

где 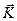- вектор обратной решетки, а вектор лежит в первой зоне Бриллюэна. Для любого вектора обратной решетки 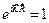, поэтому если соотношение Блоха выполняется для 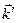, то оно справедливо и для .

Уровни энергии электрона в периодическом потенциале. Номер зоны 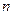появляется в теореме Блоха из-за того, что при заданном значении имеется много решений уравнения Шредингера.

Будем искать все решения уравнения Шредингера (4.6), которые могут быть представлены в блоховской форме

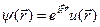(4.44)

с заданным волновым вектором и с функцией 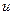, обладающей периодичностью решетки. Подставляя это выражение в уравнение Шредингера, находим, что 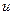определяется задачей на собственные значения

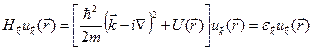(4.45)

с граничным условием

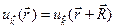. (4.46)

Благодаря периодическому граничному условию следует ожидать, что существует бесконечное семейство решений с дискретными собственными значениями, которые мы различаем с помощью номера зоны .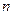

В задачу на собственные значения (4.45) и (4.46) волновой вектор входит лишь в качестве параметра гамильтониана 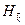. Поэтому можно считать, что энергия уровней с волновым вектором меняется непрерывно с волновым вектором . В результате мы приходим к описанию уровней энергии в периодическом потенциале посредством семейства непрерывных функций 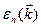. То обстоятельство, что в силу граничного условия Борна-Кармана волновой вектор может принимать лишь дискретные значения, не имеет отношения к непрерывности 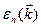как функции от непрерывной переменной , поскольку в задачу на собственные значения не входит размер всего кристалла и она имеет смысл при любом .

Поскольку для двух значений , отличающихся на вектор обратной решетки, все волновые функции и энергетические уровни совпадают, можно приписать уровням индексы 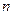таким образом, чтобы при заданном 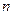собственные состояния и собственные значения представляли собой периодические функции от в обратной решетке

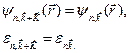(4.47)

Таким образом, энергетические уровни электрона в решетке в периодическом потенциале описываются посредством семейства непрерывных функци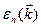й или 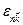, каждая из которых имеет периодичность обратной решетки. Эти функции определяют зонную структуру твердого тела.

Совокупность всех электронных уровней, описываемых функцией 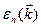при фиксированном 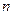, называют энергетической зоной. Каждая функция 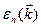периодична по и непрерывна, у нее существуют верхний и нижний пределы и все уровни 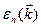лежат в зоне энергий между этими пределами.

Происхождение запрещенной зоны

 

Попытаемся понять физические причины наличия запрещенных зон, рассматривая для начала простую модель кристалла в виде линейной цепочки атомов (одномерной ре­шетки), расположенных на расстоянии а один от другого (а — постоянная решетки). Участок зонной структуры, относящийся к области низких энергий, показан схематически на рис. 9.2 для свободных электронов (рис. 9.2,а.) и почти свобод­ных электронов (рис. 9.2,б), для которых имеется энергетическая щель (запрещенная зона) при k = ± 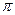/а.

 

 

Условие Брэгга для электронов имеет вид 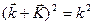и описывает дифракцию электронных волн с волновым вектором ; в одномерном случае условие Брэгга дает следующий набор значений :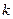

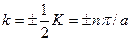
где 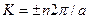— обратная длина (в общем случае — вектор обратной решетки), п — целое число. Первые отражения (и пер­вая энергетическая щель) имеют место при 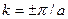( 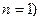; последующие энергетические щели отвечают другим значениям п, соответствующим п > 1 в (9.4). Отражение при 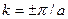получается, когда электронная волна от данного атома линейной цепочки интерферирует с волной от атомов, являющихся его ближайшими соседями. Разность фаз между двумя волнами равна как раз ±2 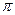для этих двух значений k . Интервал значе­ний 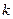между — 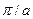и 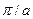называется первой зоной Бриллюэна (для одномерной моноатомной решетки).

При k = ± 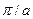волновые функции электрона уже не яв­ляются бегущими волнами вида 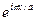и 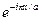, как это было в модели свободных электронов. Ниже будет показано, что ре­шения при этих частных значениях k представляют собой сово­купности равного числа волн, распространяющихся вправо и влево, т. е. являются стоячими волнами. А пока приведем лишь некоторые качественные соображения. Когда условия Брэгга удовлетворяются, можно сказать, что волна, бегущая в одном направлении, испытав брэгговское отражение, распространяет­ся затем в пpoтивоположном направлении. Каждое последую­щее брэгговское отражение вновь обращает направление рас­пространения волны. Единственной независимой от времени картиной, отвечающей такой ситуации, является картина обра­зования стоячих волн. Из бегущих волн вида 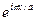и 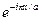, мы мо­жем сформировать две различные стоячие волны, а именно:

 

 

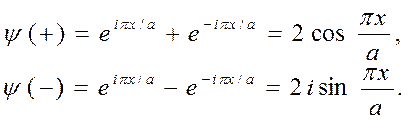
Стоячие волны состоят из бегущих - правых и левых в равных долях. Индексы (+) и (-) у стоячих воли означают соответственно четную и нечетную функции при замене 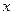на .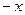

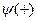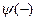Две стоячие волны и отвечают группировке электронов в различных по отношению к ионам областях пространства, а, следовательно, эти две волны имеют различные значения потенциальной энергии. Это обстоятельство и является причиной существования энергетической щели. В квантовой механике плотность вероятности 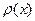нахождения частицы в точке х равна 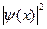. Для чисто бегущих волн функция 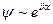и, следовательно, 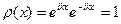, т.е. плотность заряда — постоянная вели-

чина. Но для линейной комбинации плоских волн плотность за­ряда уже не будет постоянной величиной.

Рассмотрим, например, стоячую волну 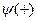; для плотности 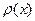в этом случае получим:

 

 

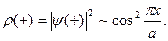
Рис. 9.3. а) Изменение потенциальной энергии электрона проводимости в поле ионных остовов в линейной цепочке. б) Распределение плотности вероятности 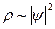для волновых функци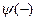й и 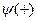электрона в линейной це­почке; 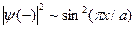, 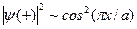. Штрих-пунктирной горизонтальной прямой показана (постоянная) плотность вероятности, соответствующая бегущей волне 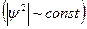. Волновая функция 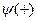дает пучности плотности электрического заряда в точках, соответствующих центрам (положительных) ионов, понижая тем самым потенциальную энергию относительно уровня ее среднего значения, отвечающего бегущей волне. Волновая функция 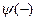дает пучности плотности заряда в областях между ионами, сдвигая их от центров ионов и повышая тем самым потенциальную энергию относительно уровня для бегущей волны. Описанная схема — ключ к понима­нию происхождения энергетической щели.

Эта функция описывает скопление отрицательного заряда на положительных ионах или вблизи них, т. е. в областях 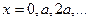, где потенциальная энергия — наименьшая. На рис. 9.3,а схематически изображен ход изменения электростати­ческой потенциальной энергии электрона проводимости в перио­дическом поле положительных ионных остовов в моноатомной линейной цепочке. Ионные остовы несут положительный заряд, поскольку цепочка состоит из атомов металла, каждый из кото­рых потерял один или более валентных электронов, которые занимают уровни зоны проводимости. Потенциальная энергия любого электрона в поле положительного иона отрицательна, т.е. cooтветствует притяжению. На рис. 9.3,б схематически изображено распределение электронной плотности в стоячих волнах 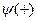и 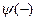; для сравнения штрих-пунктирной гори­зонтальной линией показана электронная плотность для бегу­щей волны. В стоячей волне 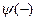для плотности вероятности имеем:

.

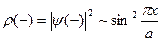Эта функция описывает такое распределение электронов, при котором они располагаются преимущественно в областях, соот­ветствующих серединам расстояний между ионами, т. е. вне ионных остовов. При расчете средней потенциальной энергии для каждого из описанных трех случаев распределения элек­тронной плотности следует ожидать, что в случае 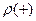сред­няя потенциальная энергия будет меньше, чем для бегущих волн, в то время как для 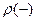она соответственно больше. Если средние значения потенциальной энергии для 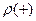и 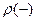раз­личаются на величину Eg, то существует энергетическая щель шириной Eg (см. рис. 9.2). Волновая функция 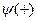(ниже энер­гетической щели) отмечает на рис. 9.2 точкам А, а волновая функция 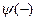(выше энергетической щели) - точкам В.

 

Поверхность Ферми. Основное состояние 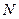свободных электронов строится путем заполнения всех одноэлектронных уровней с энергиями 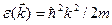, меньшими 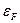, где 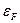определяется из условия, что полное число одноэлектронных уровней с энергией 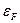, должно быть равно полному числу электронов.

Основное состояние 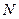блоховских электронов строится аналогичным образом, за исключением того, что одноэлектронные уровни задаются теперь квантовыми числами 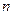и , а 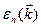уже не определяется простым выражением как в теории свободных электронов. После заполнения низших уровней определенным числом электронов могут получиться конфигурации двух различных типов.

1. Некоторые зоны могут оказаться полностью заполненными, а все остальные – пустыми. Разность энергий между самым высоким занятым уровнем и самым низким незанятым уровнем (т.е. между «вершиной» самой верхней занятой зоны и «дном» самой низкой пустой зоны) называют запрещенной зоной. Твердые тела, у которых ширина запрещенной зоны значительно больше 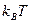, представляют собой диэлектрики. Если ширина запрещенной зоны сравнима с 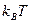, то такие твердые тела называют собственным полупроводником. Поскольку число уровней в зоне равно полному числу элементарных ячеек в кристалле и на каждом уровне могут быть размещены два электрона, то для возникновения конфигурации с запрещенной зоной необходимо, чтобы число электронов в расчете на одну элементарную ячейку было четным.

2. Некоторые зоны могут оказаться заполненными частично. Когда это имеет место, энергия наиболее высокого заполненного уровня, т.е. энергия Ферми, лежит внутри области энергий одной или более зон. В -пространстве каждой частично заполненной зоне соответствует поверхность, отделяющая занятые уровни от незанятых. Все такие поверхности называют поверхностью Ферми. Поверхность Ферми для блоховских электронов является обобщением сферы Ферми, рассмотренной ранее для свободных электронов. Части поверхности Ферми, соответствующие отдельным частично заполненным зонам, называют полостями поверхности Ферми. Аналитическое определение полости поверхности Ферми в 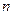-той зоне таково:

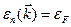. (4.48)

Следовательно, поверхность Ферми представляет собой поверхность постоянной энергии (или совокупность поверхностей постоянной энергии) в -пространстве.

Поскольку функции 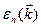периодичны в обратной решетке, полное решение уравнения (4.48) для каждого 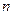представляет поверхность в -пространстве, также обладающей периодичностью обратной решетки.