Глава 3. Расчет трехфазной электрической цепи с гармоническими напряжениями и токами.

Дата: 2025-05-01; Просмотры: 2
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

Трехфазные цепи являются разновидностью цепей синусоидального тока, и, следовательно, все рассмотренные ранее методы расчета и анализа в символической форме в полной мере распространяются на них.

Многофазный приемник и вообще многофазная цепь называются симметричными, если в них комплексные сопротивления соответствующих фаз одинаковы, т.е. если 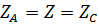. В противном случае они являются несимметричными.

Данные для расчетов: 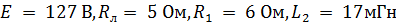, номер ключа К0.

Расчетная схема представлена на рисунке 27. Источники ЭДС образуют симметричную систему:

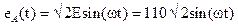
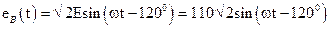
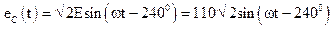
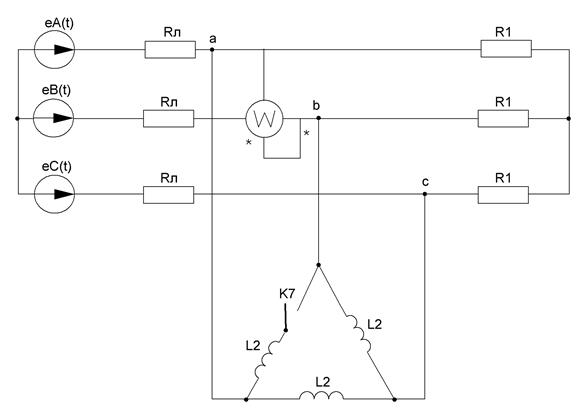
Рисунок 27 - Схема для задания №3

3.1 Расчет симметричного режима.

Если к симметричной трехфазной цепи приложена симметричная трехфазная система напряжений генератора, то в ней будет иметь место симметричная система токов. Такой режим работы трехфазной цепи называется

симметричным. В этом режиме токи и напряжения соответствующих фаз равны по модулю и сдвинуты по фазе друг по отношению к другу на угол 1200. Вследствие указанного расчет таких цепей проводится для одной – базовой – фазы, в качестве которой обычно принимают фазу А. При этом соответствующие величины в других фазах получают формальным добавлением к аргументам переменных фазы А фазового сдвига 1200 при сохранении неизменным ее модуля. [1] Следовательно, в данном пункте необходимо произвести расчет только токов и напряжений, относящихся к фазе А: 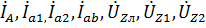, а оставшиеся получить вышеуказанным способом. Схема для расчета симметричного режима с указанием положительных направлений токов изображена на рисунке 28.

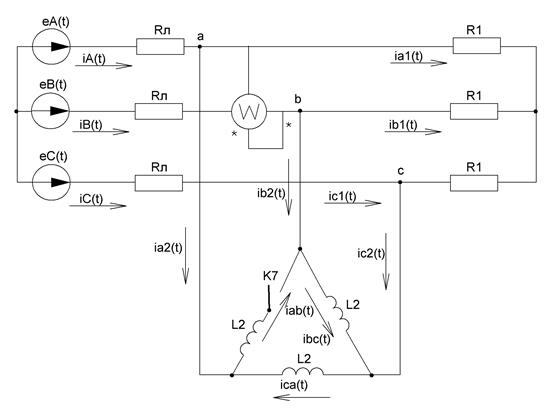
Рисунок 28 – Исходная схема для расчета при симметричном режиме

3.1.1 Расчет цепи с помощью средств программы ElectronicsWorkbench.

В вышеуказанной программе был выполнен чертеж необходимой схемы с заданными значениями сопротивлений линий, первой и второй нагрузки, источников ЭДС. В результате расчета были получены следующие модули действующих значений токов:

.

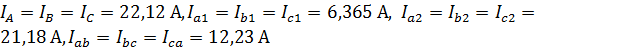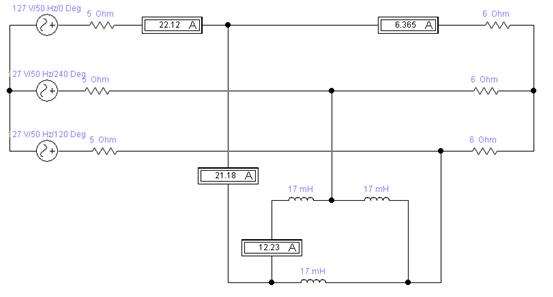
Рисунок 29 - Расчет симметричного режима трехфазной цепи с помощью средств программы ElectronicsWorkbench

3.1.2 Преобразование схемы до эквивалентной звезды и определение комплексов действующих значений напряжений и токов во всех фазах. Расчет показаний ваттметра.

1. Изобразим схему с комплексными параметрами, для чего рассчитаем комплексные сопротивления фаз: .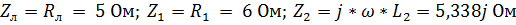

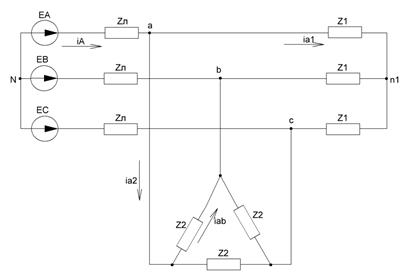
Рисунок 30 - Схема для расчета симметричного режима с комплексными параметрами

2. Осуществим эквивалентное преобразование соединения «треугольник» в «звезду», для чего рассчитаем необходимые значения сопротивлений ветвей: .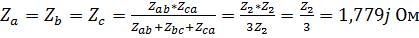

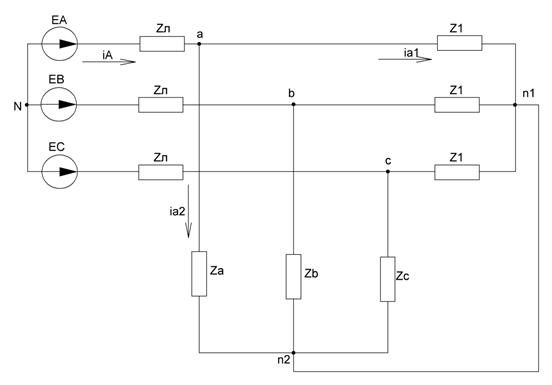
Рисунок 31 - Эквивалентное преобразование «треугольник» - «звезда»

3. Из полученной в предыдущем пункте схемы видим, что элементы первой и второй нагрузок соединены пофазно параллельно. Значит, можем преобразовать их в одно сопротивление в каждой фазе: 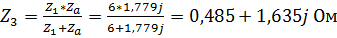. Тогда получим следующую схему для расчетов:

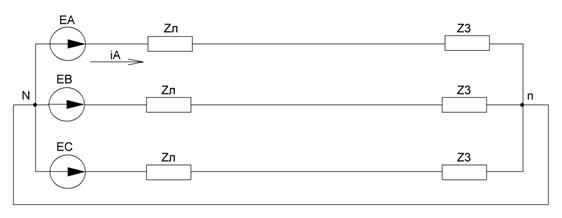
Рисунок 32 - Схема с одной нагрузкой, соединенной в «звезду»

4. Так как режим работы цепи – симметричный, то напряжение между нейтральными точками N и n отсутствует. Следовательно, можем считать, что они соединены нейтралью. Тогда из контура с нейтралью и верхней ветвью по второму закону Кирхгофа получаем:

.

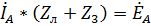Тогда сила тока в фазе А равна:

.

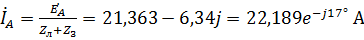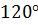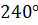Так как система симметричная, то, как отмечалось ранее, токи фаз В и С отстают по фазе от тока фазы А на и соответственно (или опережают его на 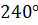и 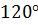). Тогда для этих токов получаем: .

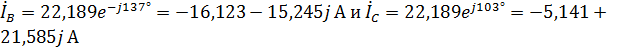5. Обратимся к схеме на рисунке 30. Найдем потенциалы точек a , b , c, приняв потенциал точки Nравным нулю.

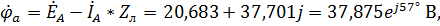
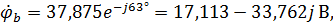
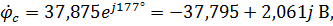
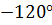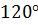где выражения для потенциалов точек bи c получены путем изменения начальной фазы потенциала точкиа на и соответственно.

6. Обратимся к схеме на рисунке 31. Потенциалы точек 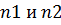равны нулю, тогда мы можем составить выражения для токов первой нагрузки. Как было указано в пункте 1.4 выражение для тока через потенциалы узлов записывается следующим образом:

.

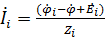Тогда составляем следующее выражение:

.

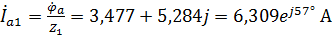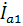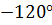Найдем оставшиеся токи первой нагрузки путем изменения начальной фазы тока на и 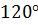соответственно:

,

.

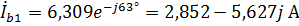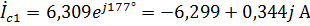7. Найдем фазные токи второй нагрузки, соединенной в «треугольник», через потенциалы :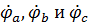

,

,

.

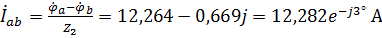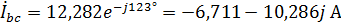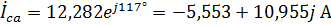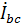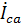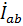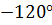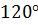Здесь значения и по модулю совпадают с , но по фазе отличаются на и соответственно.

8. Линейные токи второй нагрузки найдем по первому закону Кирхгофа. Для узлаа имеем:

.

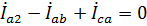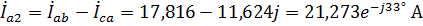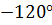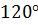Тогда искомый ток равен: . Токи фаз В и С имеют тот же модуль, но отличаются по фазе на и соответственно:

,

.

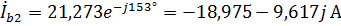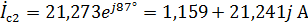9. Найдем падения напряжения на каждом комплексном элементе для фазы А:

,

,

,

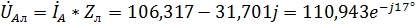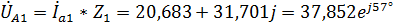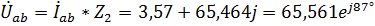где 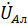– падение напряжения на элементе 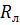, 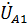- падение напряжения на элементе 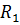, 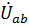- падение напряжения на элементе .

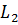Для фазы В с учетом сдвига фаз на 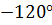относительно фазы А получаем:

,

,

.

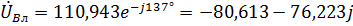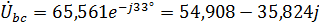Для фазы С с учетом сдвига фаз на 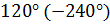относительно фазы А получаем:

,

,

.

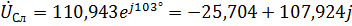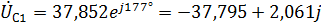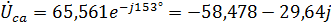Линейные напряжения нагрузки равны:

,

,

,

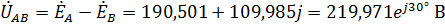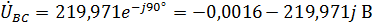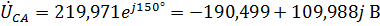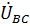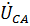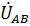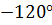где значения и получены путем изменения начальной фазы линейного напряжения на и 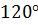соответственно.

10. Рассчитаем показания ваттметра. Они будут определяться следующей формулой:

.

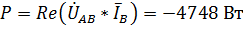где 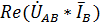– вещественная часть комплексного числа .

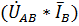3.1.3 Расчет баланса активной и реактивной мощностей

Так как система симметрична, то достаточно осуществить расчет баланса активной и реактивной мощностей только для одной фазы А.

Мощность источника в фазе А находится по формуле:

.

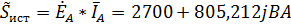Мощность потребителей: 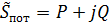, где P – активная составляющая мощности, Q – реактивная составляющая мощности.

Определим активную составляющую:

,

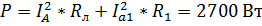где 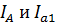– модули линейных токов источника и первой нагрузки в фазе А.

Реактивная составляющая мощности равна:

,

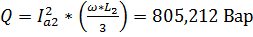где 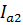– модуль линейного тока второй нагрузки в фазе А.

Тогда полная мощность, расходуемая потребителями: 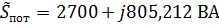. Как видим, 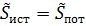, значит, значения токов найдены верно.

3.1.4 Совмещенная векторная диаграмма для токов и напряжений.

Совмещенная векторная диаграмма для токов и напряжений для рассматриваемого симметричного режима изображена на рисунке 33.

3.2 Расчет несимметричного режима.

Если хотя бы одно из условий симметрии не выполняется, в данном случае это нарушение в симметрии нагрузки, то есть 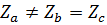, в трехфазной цепи имеет место несимметричный режим работы. Такие режимы при наличии в цепи только статической нагрузки и пренебрежении падением напряжения в генераторе рассчитываются для всей цепи в целом любым из рассмотренных ранее методов расчета. [7]

Для исходной схемы, представленной на рисунке 27, несимметричный режим получается при размыкании ключа К7. Тогда из схемы убирается один элемент второй нагрузки, соединенной в «треугольник». Полученная схема с указанием положительных направлений токов изображена на рисунке 34.

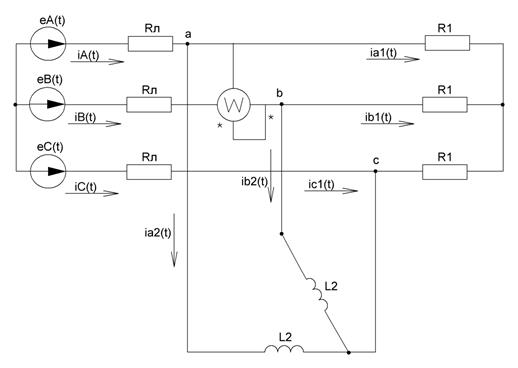
Рисунок 34 - Исходная схема для расчета несимметричного режима

3.2.1 Расчет цепи с помощью средств программы ElectronicsWorkbench.

В вышеуказанной программе был выполнен чертеж необходимой схемы с заданными значениями сопротивлений линий, первой и второй нагрузки, источников ЭДС. В результате расчета были получены следующие модули действующих значений токов:

.

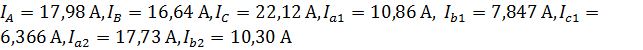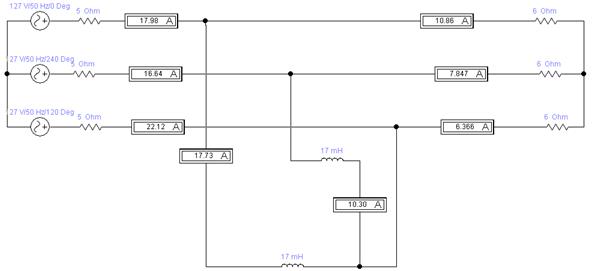
Рисунок 35 - Расчет несимметричного режима трехфазной цепи с помощью средств программы ElectronicsWorkbench

3.2.2Упрощение схемы путем последовательных преобразований трехфазных нагрузок

1. Изобразим схему с комплексными параметрами, для чего рассчитаем комплексные сопротивления элементов цепи: .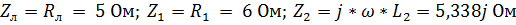

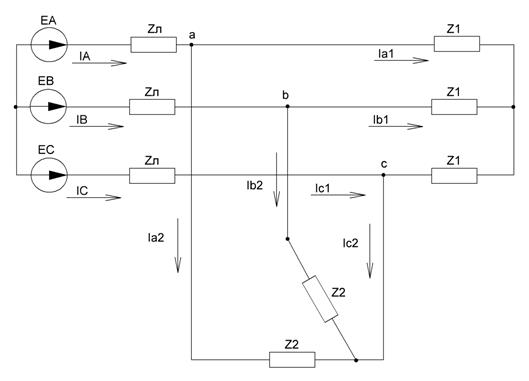
Рисунок 36 - Схема для расчета несимметричного режима с комплексными параметрами

2. Осуществим эквивалентное преобразование соединения «звезды» в «треугольник» для первой нагрузки, для чего рассчитаем необходимые значения сопротивлений ветвей: .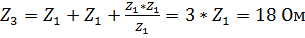

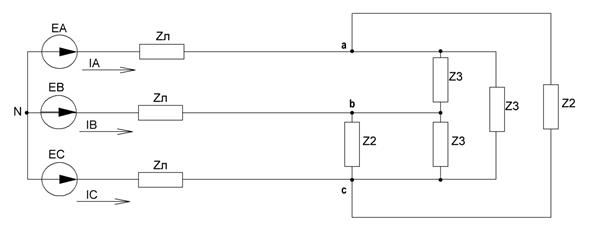
Рисунок 37 - Схема, полученная после преобразований в пункте 2

3. Преобразуем параллельно соединеные комплексные сопротивления 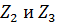в 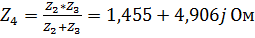. В результате получим схему, изображенную на рисунке 38.

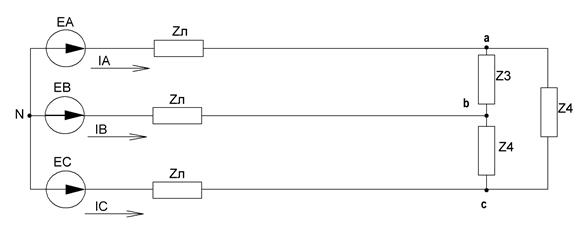
Рисунок 38 – Схема, полученная после преобразований в пункте 3

4. Выполним эквивалентное преобразование «треугольник» - «звезда», рассчитав для этого соответствующие комплексные сопротивления ветвей:

,

,

.

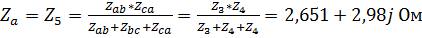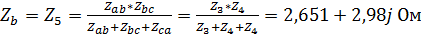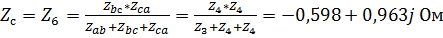После данного преобразования получаем схему, изображенную на рисунке 39.

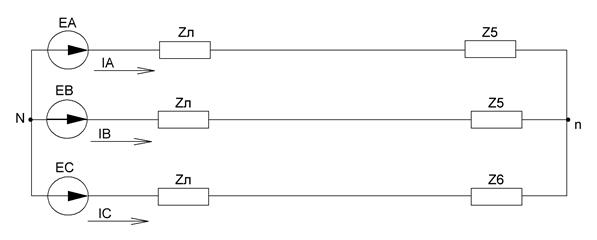
Рисунок 39 – Схема, полученная после преобразований в пункте 4

5. Преобразуем последовательно соединенные комплексные сопротивления каждой фазы в одно сопротивление:

,

.

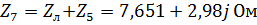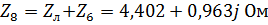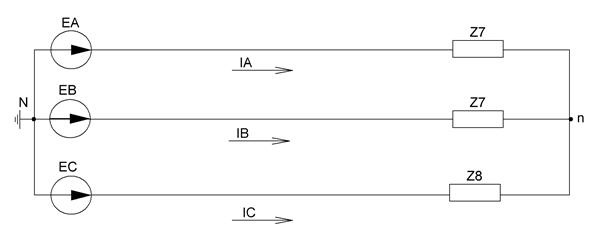
Рисунок 40 – Окончательная схема для расчетов

3.2.3 Определение комплексов действующих значений напряжений и
токов исходной схемы. Расчет показаний ваттметра.

1. Для дальнейших расчетов примем, что точка 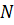заземлена. Так как рассматриваемый режим цепи – несимметричный, то найдем напряжение между нейтральными точками :

,

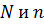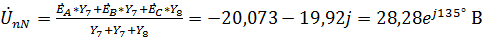где 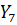и 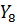– комплексные проводимости соответствующих ветвей, равные:

,

.

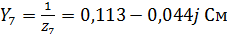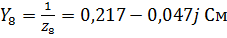2. Используя значение 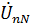, найдем фазные токи источников:

,

,

.

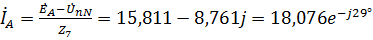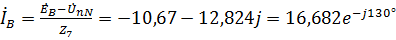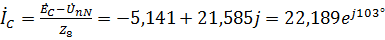3. Так как точка 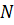заземлена, то относительно нее 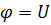. Тогда найдем потенциалы точек 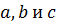относительно :

,

,

.

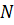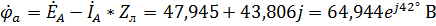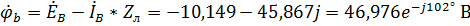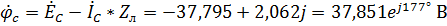4. Рассчитаем токи для схемы, представленной на рисунке 36. Линейные токи первой нагрузки будут равны:

,

,

.

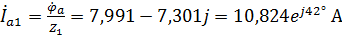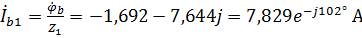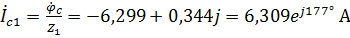Рассчитаем линейные токи второй нагрузки:

,

,

.

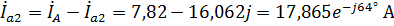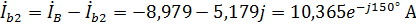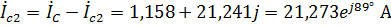5. Найдем падения напряжения на каждом комплексном элементе.

Для фазы А: ,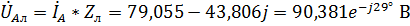

,

.

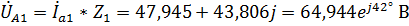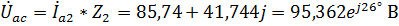Для фазы В: ,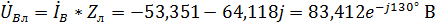

,

.

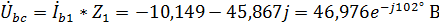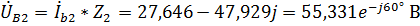Для фазы С: ,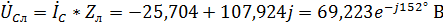

,

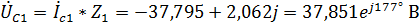Значения линейных напряжений аналогичны значениям, приведенным в симметричном режиме.

6. Рассчитаем показания ваттметра. Они будут определяться следующей формулой:

.

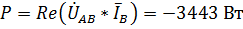где 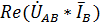– вещественная часть комплексного числа .

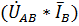3.2.4 Расчет баланса активной и реактивной мощностей

Суммарная мощность источников всех фаз равна:

,

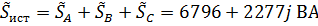где ,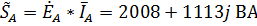

,

.

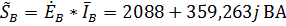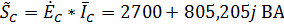Определим мощность потребителей в каждой фазе.

,

,

.

,

,

.

,

.

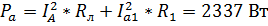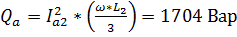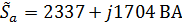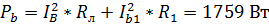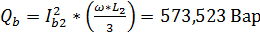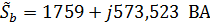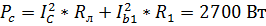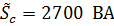Суммарная мощность потребителей: 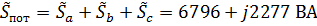. Таким образом, 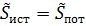, следовательно, значения токов найдены верно.

3.2.5 Совмещенная векторная диаграмма для токов и напряжений

Совмещенная векторная диаграмма для токов и напряжений для рассматриваемого несимметричного режима изображена на рисунке 41.

3.3 Анализ результатов вычислений, сравнение симметричного и несимметричного режимов

Проанализировав полученные результаты, можно отметить следующее. При расчете симметричного режима были получены значения линейных и фазных токов и напряжений, относящихся к одной нагрузке, с одинаковыми модулями и сдвигом фаз на 120 градусов друг относительно друга. Стоит отметить, что это существенно сокращает время расчетов, так как находятся только токи и напряжения, относящиеся к одной из фаз, а другие получаются путем изменения начальной фазы найденных значений на 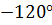и 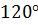. Так же сокращается время проверки полученных значений балансом мощностей, так как необходимо составить его так же только для одной фазы.

Если же говорить о несимметричном режиме, то здесь вышеуказанное условие уже не выполняется и расчет приходится производить для элементов всех фаз, так как значения фазных и линейных токов и напряжений для каждой фазы отличаются от другой как по модулю, так и по фазе на произвольное число градусов. Еще одним пунктом, усложняющим расчет такого режима, является факт смещения нейтральной точки, что в свою очередь обусловливает факт существования напряжения смещения, которое необходимо вычислить, чтобы грамотно произвести расчеты. Как следствие вышесказанного, при составлении баланса мощностей необходимо учитывать параметры трех фаз, а не одной, как в симметричном режиме.

Векторные диаграммы напряжений для данных режимов отличаются своим видом, причем для несимметричного режима этот вид определяют вид несимметрии (источники или нагрузка) и схемы соединения элементов («звезда» или «треугольник»). Однако для обоих режимов векторные диаграммы напряжений позволяют достаточно быстро определить искомое напряжение между определенными потенциалами или же фазное (линейное) напряжение нагрузки (источников). Векторные же диаграммы тока для данных режимов строятся по одному и тому же принципу – по первому закону Кирхгофа и не существенно отличаются друг от друга.

Заключение

В ходе выполнения первого задания данной курсовой работы были получены навыки расчета линейных электрических цепей постоянного тока различными способами: с применением законов Кирхгофа, методом контурных токов, методом узловых потенциалов. Эти способы позволяют найти токи во всех ветвях схемы и напряжения между ее узлами. Если же требуется найти значение тока только в одной выделенной ветви, то в данном случае можно применить метод эквивалентных преобразований или метод эквивалентного генератора. К тому же, первый метод позволяет существенно упростить исходную схему, что в свою очередь также упрощает и ее расчет.

Во втором задании были определены комплексы действующих значений и мгновенные значения силы тока в ветвях однофазной цепи переменного тока. Расчет был произведен для цепи без магнитной связи и с ней методом непосредственного применения законов Кирхгофа. Здесь отдельного внимания заслуживает именно цепь с наличием между катушками индуктивности магнитной связи, так как в данном случае при расчете приходится учитывать не только ток, непосредственно протекающий через катушку, но и ток, протекающий через катушку, магнитно связанную с ней. Следовательно, для расчета такой цепи наиболее оптимальными выступают методы непосредственного применения законов Кирхгофа и контурных токов. Наглядное представление о процессах, протекающих в электрической цепи, можно получить из векторных диаграмм напряжений, которые отражают падения напряжения на каждом элементе схемы. Поэтому и напряжение между узлами цепи в некоторых случаях также можно рассчитать с помощью данных диаграмм.

В ходе выполнения третьего задания данной курсовой работы был произведен расчет трехфазной электрической цепи в симметричном и несимметричном режимах. Расчет был произведен с помощью законов Кирхгофа и метода узловых потенциалов. Последний метод часто применяется именно для расчета трехфазных цепей, так как в данном случае удобно заземлить один из узлов (источников или нагрузки), что существенно упрощает расчеты такого рода схем.

Сравнительный анализ симметричного и несимметричного режимов показал, что первый из них существенно проще в плане расчетов, так как фазные и линейные напряжения и токи источников и нагрузки здесь сдвинуты на 120 градусов друг относительно друга пофазно, а их модули равны. В несимметричном режиме нет нормированного сдвига фаз и равенства модулей. Однако на практике чаще всего приходится иметь дело именно с несимметричными режимами, следовательно, их расчет и понимание протекающих в них физических процессов являются важной частью при изучении и расчете трехфазных цепей.

Список использованных источников

1. Теоретические основы электротехники. Часть 1. Курсовая работа : методические указания / сост. Е. Я. Глушкин ; Сиб. федер. ун-т, ХТИ – филиал СФУ. – Абакан: Ред.-изд. сектор ХТИ – филиала СФУ, 2018. – 54 с.

2. Расчет электрической цепи по законам Кирхгофа. [Электронный ресурс] //Учебные материалы. – Режим доступа: https://dprm.ru/elektrotehnika/raschet-elektricheskoj-cepi-po-zakonu-kirhgofa (14.10.2019)

3. Баланс мощностей [Электронный ресурс]// Теоретические основы электротехники. – Режим доступа: https://electroandi.ru/toe/metod/balans-moshchnostej.html (28.10.2019)

4. Сложные цепи. Метод эквивалентного преобразования схемы. [Электронный ресурс]. – Режим доступа: https://studopedia.ru/6_95867_slozhnie-tsepi-metod-ekvivalentnogo-preobrazovaniya-shemi.html(28.10.2019)

5. Теоретические основы электротехники: В 3-х т. Учебник для вузов. Том 1. – 4-е изд. / К.С. Демирчян, Л.Р. Нейман, Н.В. Коровкин, В.Л. Чечурин. – СПб.:Питер, 2004. – 463 с.: ил.

6. Бессонов Л. А. Теоретические основы электротехники. Электромагнитное поле: Учебник для электротехн., энерг., приборостроит. спец. вузов. – 8-е изд., перераб. и доп. – М.: Высш. шк., 1986. – 263 с.: ил.

7. Расчет трехфазных цепей. [Электронный ресурс]. – Режим доступа: https://toehelp.ru/theory/toe/lecture17/lecture17.html (30.11.19)