Глава 2. Расчет линейной электрической цепи с гармоническими напряжениями и токами.
Исходная схема для расчетов изображена на рисунке 17.
Данные для расчетов: E1 = 170 В, Е2 = 130 В, Е3 = 120 В, E4 = 130 B, E5 = 80 B, J = 4 A, R1 = 190 Ом, R2 = 30 Ом, R3 = 110 Ом, R4 = 40 Ом, R5 = 100 Ом, α1 = 150°, α3 = 120°, α3 = 45°, α4 = 45°, α5 = 120°, α6 = 45°, L1 = 40 мГн, L3 = 110 мГн, L5 = 10 мГн, M= 70мГн, магнитная связь между элементами L1-L3, тип связи – согласованная, С1 = 110 мкФ, С2 = 30 мкФ, С3 = 100 мкФ.
| |
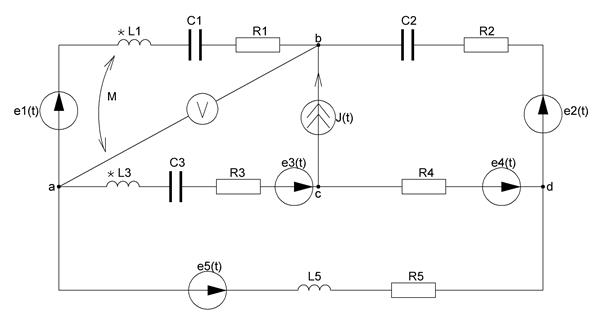
Рисунок 17 – Схема для задания №2
Символический метод расчета цепей синусоидального тока основан на законах Кирхгофа и законе Ома в комплексной форме. Уравнения, выражающие законы Кирхгофа в комплексной форме, имеют совершенно такой же вид, как и соответствующие уравнения для цепей постоянного тока. Только токи, ЭДС, напряжения и сопротивления входят в уравнение в виде комплексных величин.
Первый закон Кирхгофа для любого узла электрической цепи в комплексной форме:
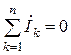
Второй закон Кирхгофа для любого контура электрической цепи в комплексной форме:

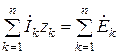
Режим работы любой цепи полностью характеризуется уравнениями, составленными на основании законов Кирхгофа. [1]
2.1 Расчет цепи с помощью программы ElectronicsWorkbench
В вышеуказанной программе был выполнен чертеж необходимой схемы с заданными значениями сопротивлений, индуктивностей, емкостей, источников тока и ЭДС без учета магнитной связи. В результате расчета были получены следующие модули действующих значений токов:
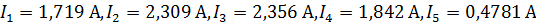 .
.
Показания вольтметров: 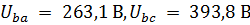 .
.
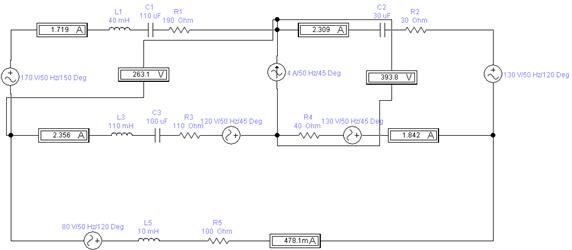
Рисунок 18 – Расчет параметров цепи без учета магнитной связи в программе ElectronicsWorkbench
2.2 Расчет по законам Кирхгофа в комплексной форме комплексов действующих значений токов всех ветвей и напряжения на зажимах источника тока без учета магнитной связи
1. Обозначим направления комплексных токов в ветвях:
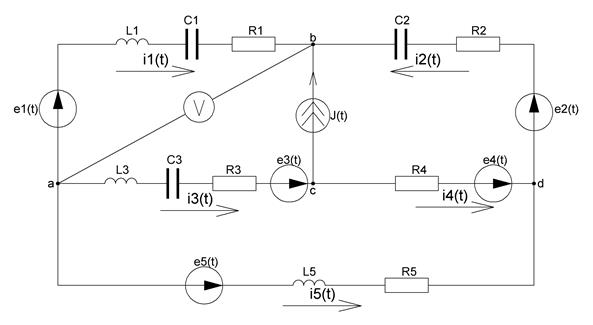
Рисунок 19 – Исходная схема для расчетов в пункте 2.2
2. Переходим к схеме с комплексными параметрами, для чего рассчитаем комплексные сопротивления ветвей:
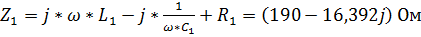 ,
,
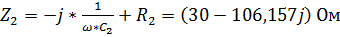 ,
,
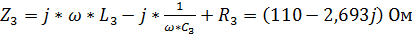 ,
,
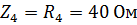 ,
,
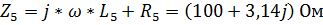 .
.
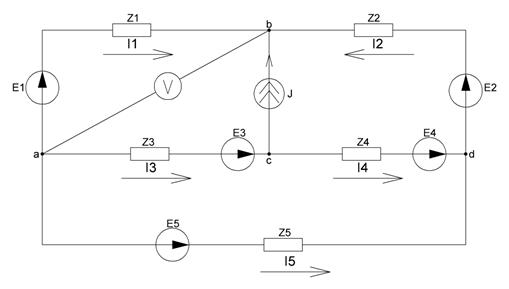
Рисунок 20 – Схема замещения с комплексными параметрами
3. Для полученной схемы составим уравнения по законам Кирхгофа, для чего проведем топологический анализ схемы. Схема содержит пять ветвей(n = 5) и четыре узла(k = 4). Следовательно, нужно составить k – 1=3 уравнения по первому закону Кирхгофа и n - (k - 1)=2 – по второму закону.
Для узлов a, b и d по первому закону Кирхгофа имеем:
Узел a) 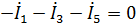 ;
;
Узел b) 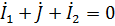 ;
;
Узел d) 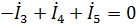 .
.
Для контуров acda и abda (направление обхода против часовой стрелки) по второму закону Кирхгофа составим следующие уравнения:
Контур acda) 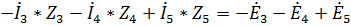 ;
;
Контур abda) 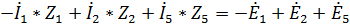 .
.
Получим систему из пяти линейных уравнений. Запишем данную систему с использованием рассчитанных ранее комплексных параметров цепи:
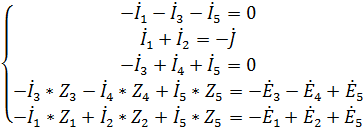 (6)
(6)
4. Решим данную систему матричным методом: 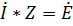
Для этого составим соответствующие матрицы:
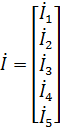 ;
; 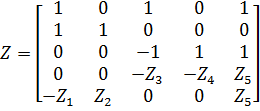 ;
; 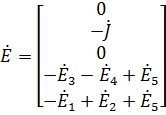 .
.
Найдём комплексные значения ЭДС и J:
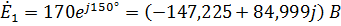 ,
,
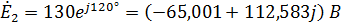 ,
,
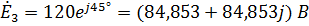 ,
,
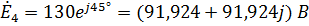 ,
,
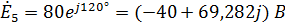 ,
,
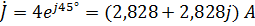 .
.
Внесем необходимые данные в программу, составленную в Mathcad для решения системы (6).

Рисунок 21 – Расчет системы (6) в программе Mathcad
Тогда комплексы токов равны:
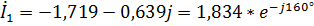 А,
А,
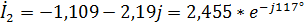 А,
А,
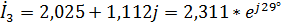 А,
А,
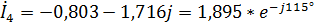 А,
А,
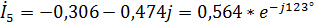 А.
А.
Найдем мгновенные значения токов, общий вид которых выглядит следующим образом:
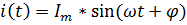 , где
, где
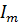 – амплитуда, равная
– амплитуда, равная 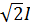 , А;
, А; 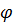 – начальная фаза в градусах.
– начальная фаза в градусах.
Тогда получим следующие мгновенные значения токов:
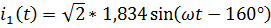 ,
,
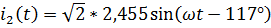 ,
,
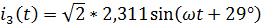 ,
,
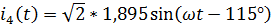 ,
,
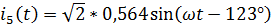 .
.
5. Найдем напряжение 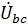 на зажимах источника тока. Для этого составим уравнение по второму закону Кирхгофа для контура bcdb (направление обхода – против часовой стрелки):
на зажимах источника тока. Для этого составим уравнение по второму закону Кирхгофа для контура bcdb (направление обхода – против часовой стрелки):
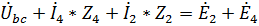
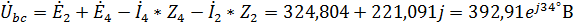 .
.
6. Проверим правильность найденных значений комплексных токов с помощью баланса активной и реактивной мощностей. Суммарная мощность источников равна:
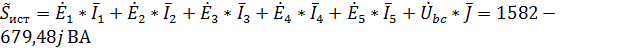 ,
,
где 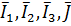 – комплексно сопряженные значения соответствующих токов.
– комплексно сопряженные значения соответствующих токов.
Суммарная мощность потребителей складывается из активной 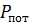 и реактивной
и реактивной 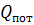 составляющих:
составляющих: 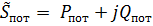 .
.
Активная составляющая:
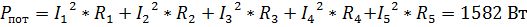 .
.
Реактивная составляющая:
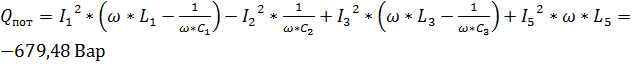 ,
,
где 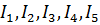 – модули комплексов токов.
– модули комплексов токов.
Тогда суммарная мощность потребителей: 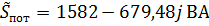 .
.
Получили, что суммарная мощность, потребляемая приемниками, равна суммарной мощности, отдаваемой источниками. Следовательно, комплексы токов найдены верно.
2.3 Расчет по законам Кирхгофа в комплексной форме комплексов действующих значений токов всех ветвей и напряжения на зажимах источника тока с учетом магнитной связи
В состав электрических цепей могут входить катушки, магнитно-связанные с другими катушками. Поток одной из них пронизывает другие и наводит в них ЭДС взаимоиндукции, которые должны быть учтены при расчете.
Степень индуктивной связи элементов характеризуется коэффициентом связи:
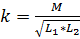 ,
,
где 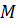 – взаимная индуктивность элементов цепи;
– взаимная индуктивность элементов цепи; 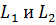 – собственные индуктивности этих элементов. [6]
– собственные индуктивности этих элементов. [6]
1. Обозначим направления комплексных токов в ветвях и согласованную магнитную связь между элементами 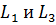 :
:
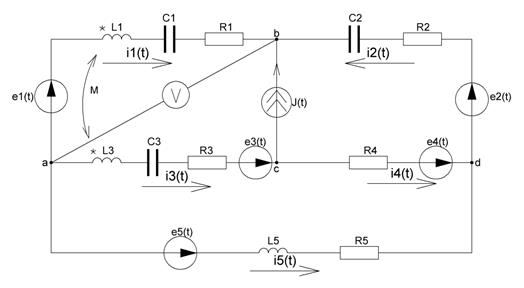
Рисунок 22 - схема для расчетов в пункте 2.3
2. Переходим к схеме с комплексными параметрами, для чего рассчитаем комплексные сопротивления ветвей:
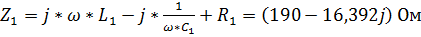 ,
,
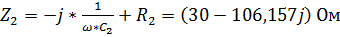 ,
,
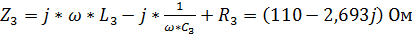 ,
,
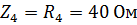 ,
,
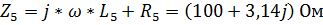 .
.
Также найдем слагаемое для магнитной связи: 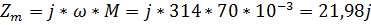
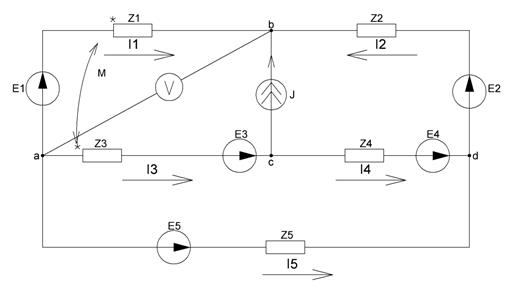
Рисунок 23 - Схема замещения с комплексными параметрами
3. Аналогично действиям в пункте 2.1, составим систему уравнений по законам Кирхгофа. Для узлов a, b и c по первому закону Кирхгофа получаем аналогичные уравнения:
Узел a) 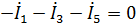 ;
;
Узел b) 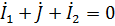 ;
;
Узел d) 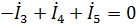 .
.
Для контуров acda и abda (направление обхода против часовой стрелки) по второму закону Кирхгофа с учетом магнитной связи составим следующие уравнения:
Контур acda) 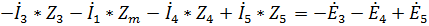 ;
;
Контур abda) 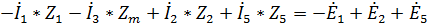 .
.
Получим систему уравнений следующего вида с комплексными параметрами цепи, рассчитанными ранее:
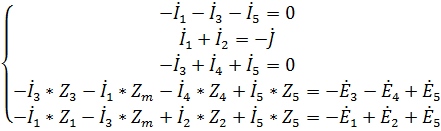 (7)
(7)
4. Решим данную систему матричным методом: 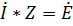 (7)
(7)
Для этого составим соответствующие матрицы:
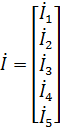 ;
; 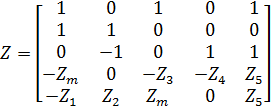 ;
; 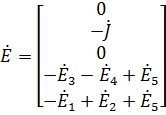 .
.
Внесем необходимые данные в программу, составленную в Mathcad для решения системы (7).

Рисунок 24 – Расчет системы (7) в программе Mathcad
Тогда комплексы токов равны:
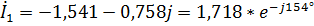 А,
А,
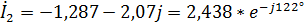 А,
А,
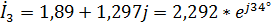 А,
А,
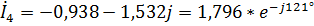 А,
А,
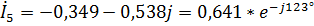 А.
А.
Найдем мгновенные значения токов:
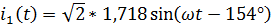 ,
,
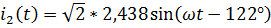 ,
,
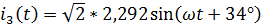 ,
,
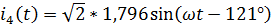 ,
,
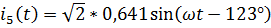 .
.
5. Найдем напряжение 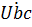 на зажимах источника тока. Для этого составим уравнение по второму закону Кирхгофа для контура bcdb(направление обхода – против часовой стрелки):
на зажимах источника тока. Для этого составим уравнение по второму закону Кирхгофа для контура bcdb(направление обхода – против часовой стрелки):
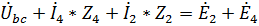 ,
,
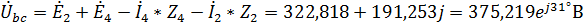 .
.
6. Проверим правильность найденных значений комплексных токов с помощью баланса активной и реактивной мощностей. Суммарная мощность источников равна:
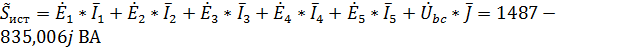 ,
,
Суммарная мощность потребителей складывается из активной  и реактивной
и реактивной 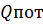 составляющих:
составляющих: 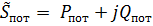 .
.
Активная составляющая:
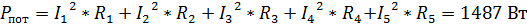 .
.
Реактивная составляющая:
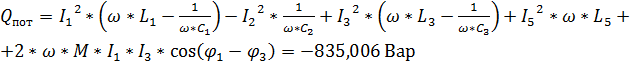 .
.
Тогда суммарная мощность потребителей: 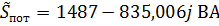 .
.
Суммарная мощность, потребляемая источниками, равна суммарной мощности, отдаваемой источниками. Следовательно, комплексы токов найдены верно.
2.4 Показание вольтметра
2.4.1 Случай без учета магнитной связи
Для нахождения напряжения 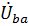 , рассмотрим контур bab и составим для него уравнение по второму закону Кирхгофа в комплексной форме:
, рассмотрим контур bab и составим для него уравнение по второму закону Кирхгофа в комплексной форме:
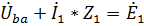
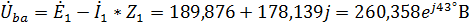 .
.
Тогда показания вольтметра: 260,358 В.
2.4.2 Случай с учетом магнитной связи
Аналогично, из того же уравнения по второму закону Кирхгофа для контура bab, имеем:
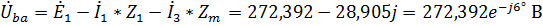 .
.
Тогда показания вольтметра: 489,917 В.
2.5 Построение векторной диаграммы токов и векторной диаграммы напряжений по результатам расчетов.
2.5.1 Для цепи без учета магнитной связи
Для построения векторной диаграммы напряжений найдем падения напряжения на элементах цепи:
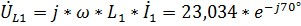 ,
,
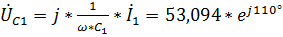 ,
,
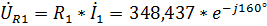 ,
,
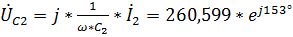 ,
,
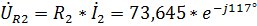 ,
,
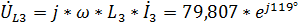 ,
,
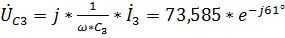 ,
,
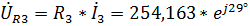 ,
,
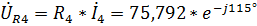 ,
,
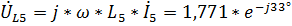 ,
,
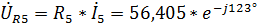 .
.
Векторная диаграмма токов и напряжений изображена на рисунке 25.
2.5.2 Для цепи с магнитной связью
Для построения векторной диаграммы напряжений найдем падения напряжения на элементах цепи:
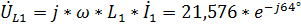 ,
,
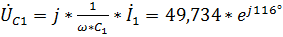 ,
,
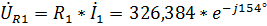 ,
,
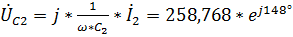 ,
,
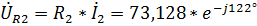 ,
,
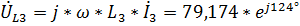 ,
,
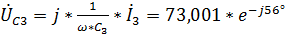 ,
,
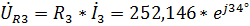 ,
,
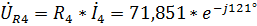 ,
,
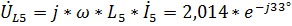 ,
,
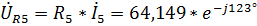 ,
,
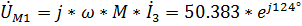 ,
,
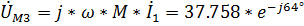 .
.
Векторная диаграмма токов и напряжений изображена на рисунке 26.








