Глава 1. Расчет линейной электрической цепи с постоянными напряжениями и токами

Дата: 2025-05-01; Просмотры: 2
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

Данные для расчета линейной электрической цепи: E1 = 170 В, Е2 = 130 В, Е3 = 120 В, E4 =130 B, E5 = 80 B, J = 4 A, R1 = 190 Ом, R2 = 30 Ом, R3 = 110 Ом, R4 = 40 Ом, R5 = 100 Ом.

Исходная cхема для расчета линейной электрической цепи представлена на рисунке 1.

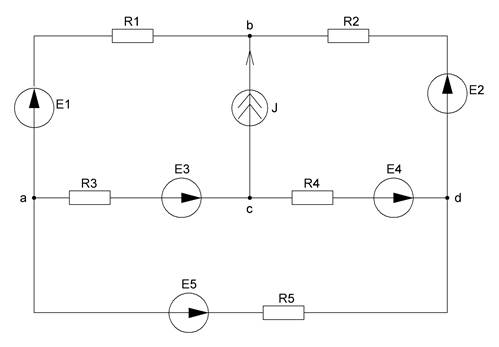
Рисунок 1 – Схема для задания 1

1.1 Расчет цепи с помощью средств программы ElectronicsWorkbench

Для проверки расчетных данных используем результат моделирования схемы в вышеуказанной программе. В результате расчета были получены следующие значения токов и напряжений:

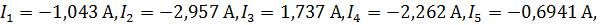
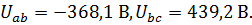
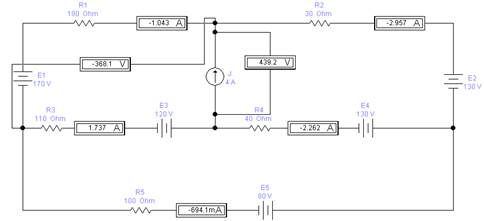
Рисунок 2 – Расчет параметров цепи в EWB

1.2 Расчет цепи методом, основанным на законах Кирхгофа:

Согласно первому закону Кирхгофа алгебраическая сумма токов ветвей, сходящихся в узле, равна нулю:

.

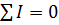Согласно второму закону Кирхгофа алгебраическая сумма напряжений на резистивных элементах замкнутого контура равна алгебраической сумме ЭДС, входящих в этот контур:

.

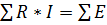1-й закон Кирхгофа применяют к независимым узлам, т.е. таким, которые отличаются друг от друга хотя бы одной новой ветвью, что позволяет получить (m - 1) уравнений.

Недостающие уравнения в количестве n - (k - 1) составляют, исходя из второго закона Кирхгофа. Уравнение записывают для независимых контуров, которые отличаются один от другого, по крайней мере, одной ветвью. [2]

1. Проведем топологический анализ:

Схема содержит пять ветвей(n = 5) и четыре узла(k = 4). Следовательно, нужно составить k – 1=3 уравнения по первому закону Кирхгофа и n - (k - 1)=2 – по второму закону.

2. Укажем направления действительных токов и направления обхода независимых контуров:

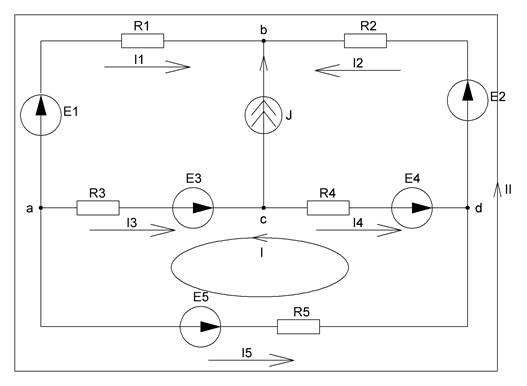
Рисунок 3 – Исходная схема для расчетов с обозначенными независимыми контурами

3. Составим три уравнения по первому закона Кирхгофа для следующих узлов:

Узел a) ;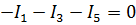

Узел b) ;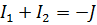

Узел d) .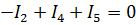

Уравнения для контуров по второму закону выглядят следующим образом:

Контур I) ;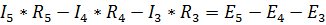

Контур II)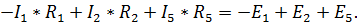

Получим систему из пяти линейных уравнений:

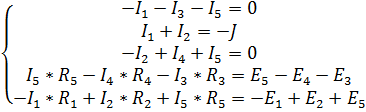(1)

4.Решим данную систему матричным методом: 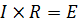, где

, , .

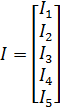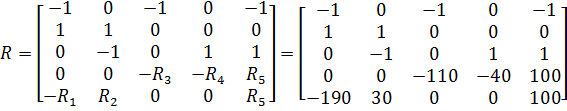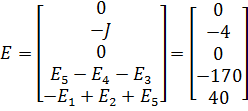Найдем значения токов с помощью программы Mathcad.

Рисунок 4 – Решение системы уравнений (1) с помощью Mathcad

Тогда токи равны: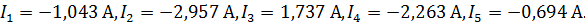

5. Напряжение 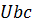на зажимах источника тока найдем из контура 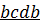(направление обхода – против часовой стрелки). По второму закону Кирхгофа:

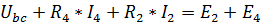
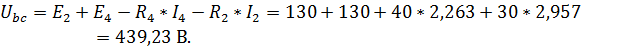
6. Определим показания вольтметра, для чего составим уравнение по второму закону Кирхгофа для контура 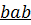(направление обхода – по часовой стрелке): 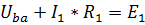. Откуда искомое напряжение равно: .

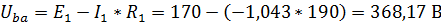1.3 Расчет цепи методом контурных токов

При расчете цепи методом контурных токов выдвигаются два предположения:

- в каждом контуре протекают независимые друг от друга расчетные (контурные) токи;

- для каждого контура с неизвестным током составляется уравнение по второму закону Кирхгофа.[2]

1. Проведем топологический анализ

Схема содержит шесть ветвей(n = 6) и четыре узла(k = 4). Следовательно, число независимых контуров равно трем: n - (k - 1)=3

Выберем независимые контуры и обозначим направления контурных токов в них:

Контур acba) – J 1=J;

Контур adca) – J 2;

Контур adba ) – J 3.

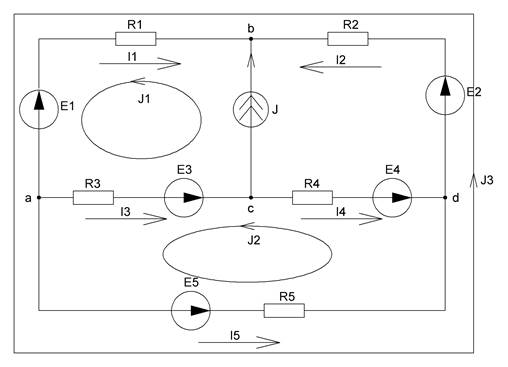
Рисунок 5 – Схема с обозначенными контурными токами

2. Для нахождения J2 и J 3 составим следующую систему уравнений по второму закону Кирхгофа:

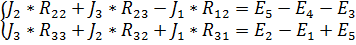
Найдем значения собственных сопротивлений контуров:

,

.

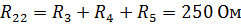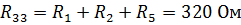Найдем значения общих сопротивлений:

,

,

,

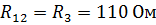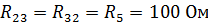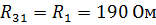Подставим полученные данные в систему (2):

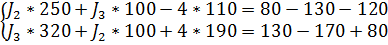
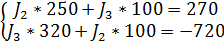
3. Решим данную систему матричным методом: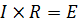

Для этого составим соответствующие матрицы:

; ; .

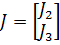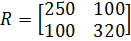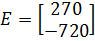Найдем значения контурных токов с помощью программы Mathcad.

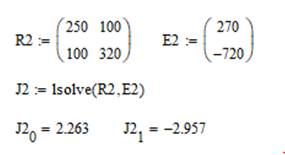
Рисунок 6 – Решение системы уравнений (2) с помощью Mathcad

Тогда контурные токи равны: .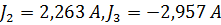

4. Запишем выражения для нахождения действительных токов и, подставив значения контурных токов, вычислим:

,

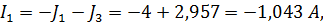
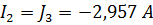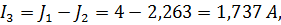
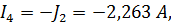
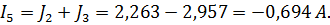
1.4 Расчет цепи методом узловых потенциалов

Данный метод основам на том, что нам нужно найти все потенциалы электрической цепи, а далее уже найти величину тока, протекающего по каждой ветви по закону Ома. Так как любой узел в электрической цепи мы можем заземлить, то для этого метода нужно составить 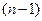уравнений, где 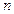- количество узлов электрической цепи.

1. Расчет произведем для схемы, изображенной на рисунке 3.

2. Обозначим потенциалы узлов 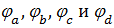. Выберем узел c и положим, что его потенциал равен нулю: 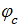= 0.

3. Запишем уравнения для узлов a, b и d в соответствии с первым законом Кирхгофа:

Узел ;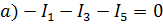

Узел ;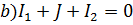

.

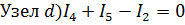4. Используя обобщённый закон Ома составим систему уравнений для нахождения токов (за 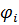берем потенциал узла из которого ток выходит, а за 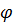потенциал узла в который ток входит, 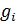– проводимость i-ой ветви).

В общем виде:

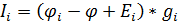
Для искомых токов получим:

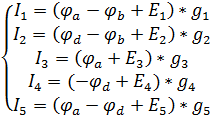(3)

5. Подставим полученные выражения для токов в уравнения из пункта 3, получим следующую систему уравнений:

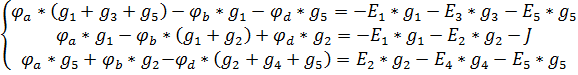(4), где

, , , , .

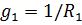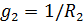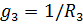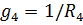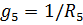6. Решим систему (4) матричным методом: .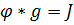

Для этого составим соответствующие матрицы:

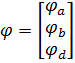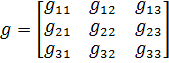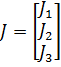; ; , где

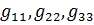– собственные проводимости:

, , ;

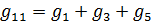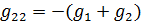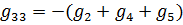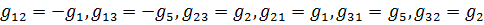– проводимости смежных узлов;

;

;

.

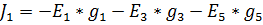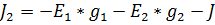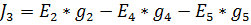Найдем решение составленной системы с помощью программы Mathcad.

Рисунок 7 – решение системы уравнений (4) в Mathcad

Найденные значения потенциалов равны:

.

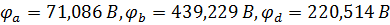Подставляя полученные значения 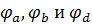в систему (3), получим следующие значения токов:

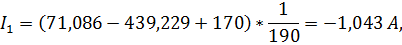
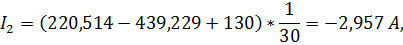
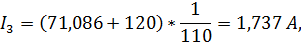
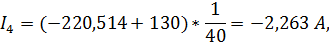
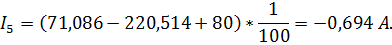
1.15 Составление баланса выделяемой и потребляемой мощностей

Баланс мощностей – это выражение закона сохранения энергии, в электрической цепи. Определение баланса мощностей звучит так: сумма мощностей потребляемых приемниками, равна сумме мощностей отдаваемых источниками.[3]

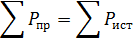
или .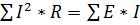

Составим баланс мощностей для схемы, указанной в задании:

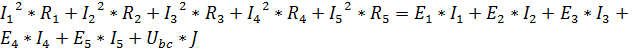. (5)

Подставляем числовые данные в выражение (5):

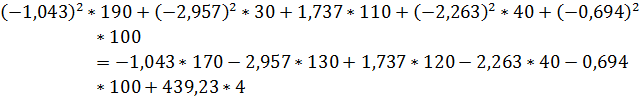
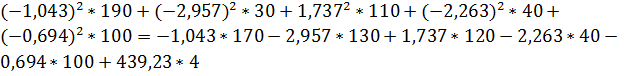
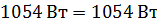
Мощность, потребляемая резисторами, равна мощности, отдаваемой источниками. Следовательно, значения токов определены верно.

1.6 Расчет тока в ветви ab методом эквивалентных преобразований электрических схем

Суть метода эквивалентного преобразования схемы заключается в упрощении схемы, когда два (или несколько) однотипных элемента электрической цепи замещаются одним эквивалентным элементом того же типа. Под термином "эквивалентный элемент" подразумевается такой элемент, замещение на который не меняет значений токов и напряжений в остальной части электрической цепи. [4]

Расчет произведем для схемы, изображенной на рисунке 1.

1. Заменим источник тока J на два таких же источника: один направлен из узла с в узел d, другой – из узла d в узел b.

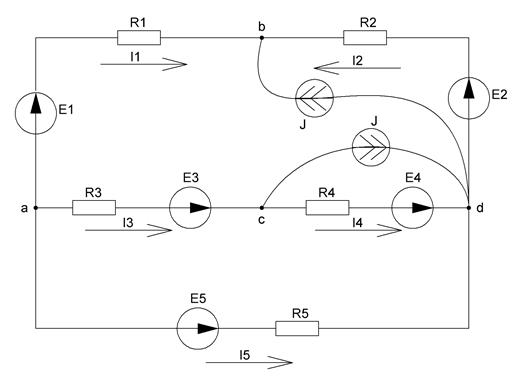
Рисунок 8 – Схема, полученная после преобразования в пункте 1

2. Заменяем последовательно соединенные резистор 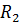и источник ЭДС 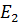на параллельно соединенные резистор того же номинала 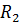и источник тока 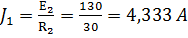. Аналогично заменяем последовательно соединенные R 4 и E 4 на параллельно соединенные R 4 и .

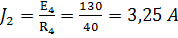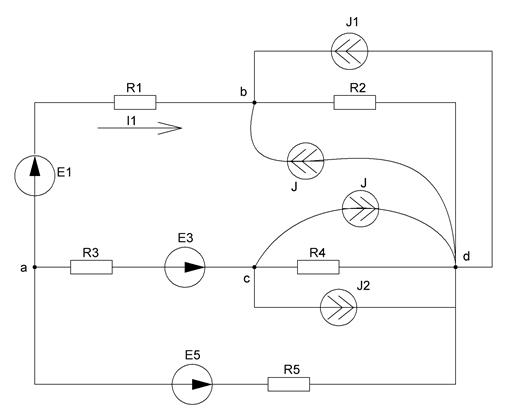
Рисунок 9 – Схема, полученная после преобразований в пункте 2

3. Заменяем параллельно соединенные J и J 1 на 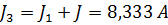. Аналогично заменяем параллельно соединенные J и J 2 на .

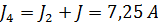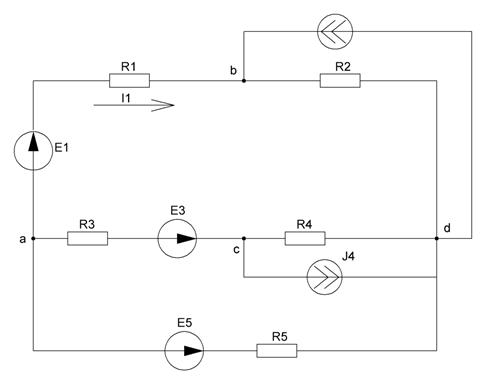
Рисунок 10 – Схема, полученная после преобразований в пункте 3

4. Заменяем параллельно соединенные резистор 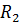и источник тока 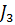на последовательно соединенные резистор того же номинала 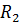и источник ЭДС 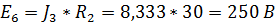. Аналогично заменяем параллельно соединенные 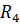и 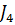на последовательно соединенные резистор того же номинала 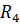и источник ЭДС .

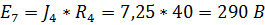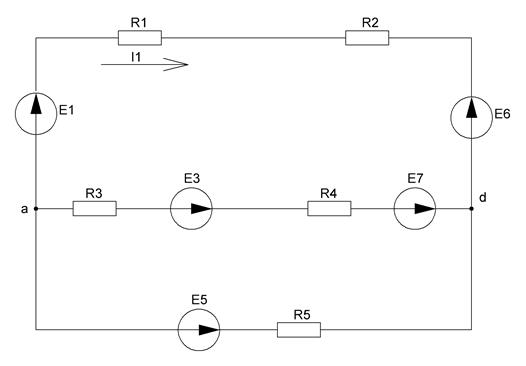
Рисунок 11 – Схема, полученная после преобразований в пункте 4

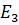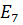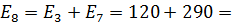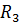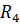5. Заменим последовательно соединенные источники ЭДС и на 410 B . Заменим последовательно соединенные резисторы и на 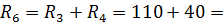150 Ом.

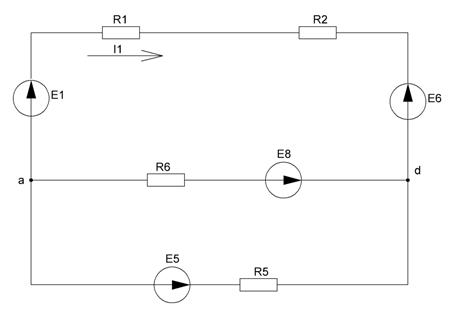
Рисунок 12 – Схема, полученная после преобразований в пункте 5

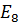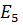6. Заменим параллельно соединенные источники ЭДС и на .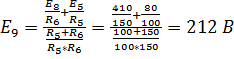

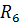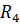Заменим параллельно соединенные резисторы и на .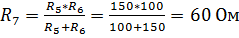

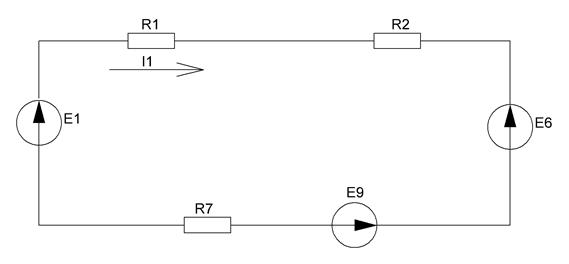
Рисунок 13 – Схема, полученная после преобразований в пункте 6

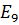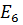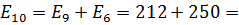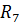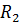7. Заменим последовательно соединенные источники ЭДС и на 462 B . Заменим последовательно соединенные резисторы и на 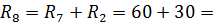90 Ом.

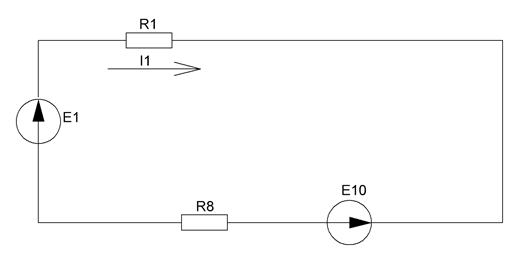
Рисунок 14 – Схема, полученная после преобразований в пункте 7

8. Для нахождения силы тока 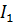составим уравнение по второму закону Кирхгофа, обходя получившийся контур по часовой стрелке:

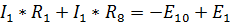
Откуда искомый ток .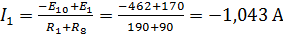

1.7 Расчет тока в ветви ab методом эквивалентного генератора

Сущность этого метода заключается в том, что по отношению к выделенной ветви ab с сопротивлением 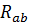вся остальная часть сложной цепи, содержащая источники ЭДС, может быть заменена одним эквивалентным генератором с ЭДС 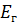и внутренним сопротивлением .

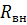Таким образом, для определения тока 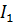в интересующей нас ветви необходимо найти напряжение 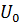при разрыве ветви ab и сопротивление 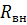всей прочей части цепи при замкнутых накоротко содержащихся в ней источниках ЭДС. [5]

1. Найдем 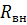, рассматривая исходную схему как активный двухполюсник относительно зажимов a и b. Для нахождения сопротивления убираем ветвь cb с источником тока и закорачиваем источники ЭДС:

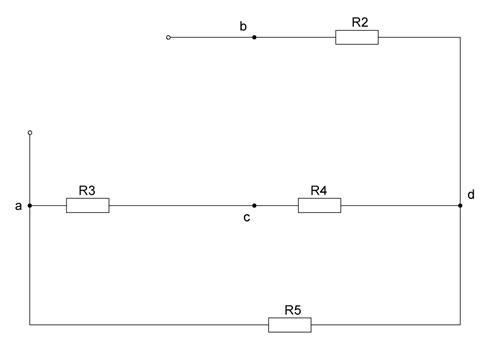
Рисунок 15 – Схема для нахождения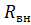

Тогда .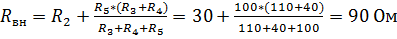

2. Найдем напряжение 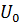на зажимах генератора, для чего убираем из схемы резистор с сопротивлением .

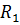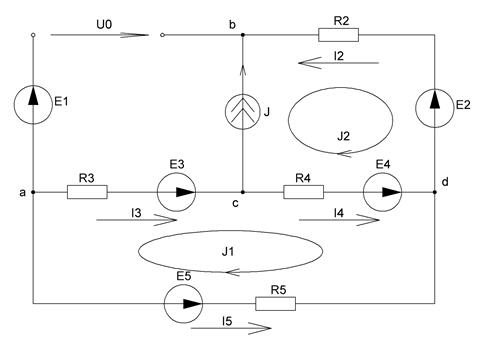
Рисунок 16 – Схема для нахождения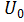

Найдем токи 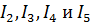методом контурных токов. Для этого выберем два контура:bdcbс контурным током 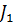и acdaс контурным током 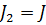. Так как значение тока во втором контуре известно, составим уравнение для нахождения контурного тока :

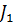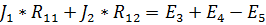, где

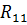– собственное сопротивление контура bdcb, равное сумме сопротивлений, входящих в этот контур: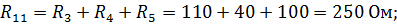

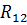– сопротивление смежной ветви контуров bdcb и acda, равное .

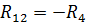Тогда значение тока 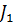можно найти из следующего выражения:

.

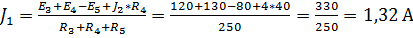Действительные токи равны соответственно: .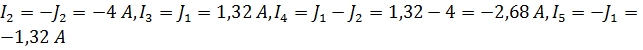

Напряжение 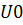найдем из контура bdcabпри обходе его по часовой стрелке. По второму закону Кирхгофа для этого контура имеем: .

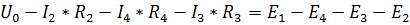Откуда .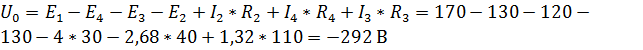

Тогда сила тока в ветви ab будет равна: 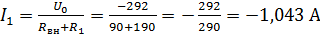.