9. Кодирование чисел в компьютере
И ДЕЙСТВИЯ НАД НИМИ
Способы кодирования и допустимые над ними действия различны для следующих числовых множеств:
· целые положительные числа (целые числа без знака);
· целые числа со знаком;
· вещественные нормализованные числа.
9.1. Кодирование и обработка в компьютере целых чисел без знака
Для записи числа в устройствах компьютера выделяется фиксированное количество двоичных разрядов.
Память компьютера имеет байтовую структуру, однако, размер одной адресуемой ячейки обычно составляет несколько байт.
Например, ячейка памяти объединяет 2 байта (16 двоичных разрядов) - такая комбинация связанных соседних ячеек, обрабатываемая совместно, называется машинным словом.
Для представления числа в регистре арифметико-логического устройства процессора, где формируется результат операции, имеется еще один дополнительный одноразрядный регистр, который называется регистром переноса и который можно рассматривать в качестве продолжения (т.е. 17-го бита) регистра результата.
Назначение этого бита выяснится чуть позже.
Конечный размер разрядной сетки порождает понятие "наибольшее целое число", которого в обычном (немашинном) представлении чисел просто не существует.
Если количество разрядов k и основание системы счисления p=2, то (Z2)max = 2k - 1.
В частности, при k=16 (Z2)max = 216 - 1 = 111 1111 1111 11112 =6553510.
Таким образом, целого числа, например 65636 и более в компьютере просто не может существовать и, следовательно, появление в ходе вычислений чисел, превышающих (Z2)max, должно интерпретироваться как ошибка.
Минимальным целым числом в беззнаковом представлении является (Z2)min = 000 0000 0000 00002 = 010.
В языке программирования PASCAL целые числа без знака, для записи которых отводится 2 байта, определены как тип Word.
Тип числа устанавливает способ кодирования этого числа, то есть количество отводимых для записи ячеек памяти (т.е. разрядность числа), а также перечень допустимых операций при обработке.
Выход за границу 65535 возможен только путем увеличения количества разрядов для записи числа, но это порождает новый тип со своим Zmax; например, тип Longint ("целое число со знаком") с максимальным значением 214748364710, числа которого занимают 4 байта.
С беззнаковыми числами выполняются арифметические операции, не меняющие типа числа; к которым относятся сложение и умножение.
Сложение
Сложение производится согласно таблице сложения, которая для двоичных чисел имеет вид:

В последнем случае в том разряде, где находились слагаемые, оказывается 0, а 1 переносится в старший разряд и называется битом переноса..
Пример 1. Найти сумму 159410 + 1756310 при беззнаковой двоичной кодировке и 16-битном машинном слове.
После перевода слагаемых в двоичную систему счисления и выполнения сложения получим (для удобства восприятия 16-ти разрядное число разобьем на группы по четыре разряда):
1 11 --Переносы
0010 0110 1001 0100
0011 0000 0011 1001
0 0101 0110 1100 1101
Рег. переполнения
Пример 2. Найти сумму 6553410 + 310
1111 1111 1111 11 ---Переносы
1111 1111 1111 1110
0000 0000 0000 0011
1 0000 0000 0000 0001
Рег. переполнения
В последнем примере в результате сложения получилось число, превышающее максимально возможное, то есть результат ошибочен, о чем свидетельствует появление 1 в регистре переполнения.
Возникновение такой ситуации в ходе выполнения программы, написанной на языке, где предусмотрено строгое описание типа переменных, приводит к прекращению работы и выводу сообщения об ошибке.
В программах, предназначенных для обработки числовой информации (например, Excel, MathCAD или Calc), при переполнении разрядной сетки производится автоматическое преобразование целого числа в вещественный тип.
Таким образом, регистр переполнения в данном случае служит индикатором корректности процесса вычислений.
Умножение
Умножение производится согласно таблице умножения, которая для двоичных чисел имеет следующий вид:
0 · 0 = 0
0 · 1 = 0
1 · 0 = 0
1 · 1 = 1
Пример 1. Найти произведение 1310 × 510 . После перевода сомножителей в двоичную систему счисления получим
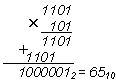
Таким образом, умножение двоичных чисел сводится к операциям сдвига на один двоичный разряд влево и повторения первого сомножителя в тех разрядах, где второй сомножитель содержит 1, и сдвига без повторения в разрядах с 0.
Сдвиг всегда чередуется со сложением из-за ограниченности числа регистров, которые имеются в процессоре для размещения операндов. Другими словами, реализации отдельной операции умножения в процессоре не требуется.
Как и в операции сложения, при умножении чисел с ограниченной разрядной сеткой может возникнуть переполнение. Решается проблема рассмотренными выше способами.
9.2. Кодирование и обработка в компьютере целых чисел со знаком
Кодирование целых чисел, имеющих знак, можно осуществить двумя способами.
В первом варианте один (старший) разряд машинном слове отводится для записи знака числа;
При этом условились кодировать знак "+" нулем, знак "–" - единицей.
Под запись самого числа, очевидно, остается 15 двоичных разрядов, что обеспечивает наибольшее значение числа Zmax = 215 - 1 = 3276710.
Такое представление чисел называется прямым кодом.
Однако его применение усложняет порядок обработки чисел;
Например, операция сложения двух чисел с разными знаками должна быть заменена операцией вычитания меньшего из большего с последующим присвоением результату знака большего по модулю числа.
Другими словами, операция сопровождается большим количеством проверок условий и выработкой признаков, в соответствии с которыми выбирается то или иное действие.
Альтернативным вариантом является представление чисел со знаком в дополнительном коде.
Идея построения дополнительного кода заключается в следующем:
· на оси целых положительных чисел, помещающихся в машинное слово (0÷65535), сместим положение "0" на середину интервала;
положительные 0 отрицательные
 |
0 32767,32768 65535
· числа, попадающие в первую половину (0÷32767) будем считать положительными, а числа из второй половины (32768÷65535) - отрицательными.
В этом случае судить о знаке числа можно будет по его величине и в явном виде выделение знака не потребуется.
Например, число 100 0000 0000 00012 = 3276910 является кодом отрицательного числа,
А число 000 0000 0000 00012 = 110 - кодом положительного.
Принадлежность к интервалу кодов положительных или отрицательных чисел видна по состоянию старшего бита кодов:
· у положительных чисел его значение "0",
· у отрицательных - "1".
Это напоминает представление со знаком, но не является таковым, поскольку используется другой принцип кодирования. Его применение позволяет заменить вычитание чисел их суммированием в дополнительном коде.
Дополнением (D) k-разрядного целого числа Z в системе счисления p называется величина
D (Zp , k) = pk - Z.
Данную формулу можно представить в ином виде:
D(Zp, k) = ((pk - 1) - Z) + 1.
Число pk - 1, состоит из k наибольших в данной системе счисления цифр (p - 1), например, 999910, FFFF16 или 11112.
Поэтому (pk - 1) - Z можно получить путем дополнения до p-1 каждой цифры числа Z и последующим прибавлением к последнему разряду 1.
Пример 1. Построить дополнение числа 27810. В данном случае p = 10, k = 3.
D(27810 , 3) = {(9-2) (9-7) (9-8)}+1, т.е. 721+1=722.
Важным свойством дополнения является то, что его сумма с исходным числом в заданной разрядной сетке будет равна 0.
В рассмотренном примере:
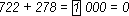
В разряде тысяч 1 должна быть отброшена, поскольку она выходит за отведенную разрядную сетку.
Так как в двоичной системе счисления дополнением 1 является 0, а дополнением 0 является 1, построение D(Z2, k) сводится к инверсии данного числа, т.е. замена нулей единицами и единиц нулями, и прибавлением 1 к последнему разряду.
Другими словами, дополнение двоичного числа формируется в два этапа:
1. Строится инвертированное представление исходного числа;
2. К инвертированному представлению прибавляется 1 по правилам двоичной арифметики.
Дополнительный код (DK) двоичных целых чисел строится по следующим правилам:
для Z2 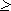 0 дополнительный код совпадает с самим числом (DK = Z2);
0 дополнительный код совпадает с самим числом (DK = Z2);
для Z2<0 дополнительный код совпадает с дополнением модуля числа, т.е. DK = D(|Z2| ,k).
Пример 14. Построить дополнительные двоичные коды чисел
(a) 310
(b) -310.
(a) Так как Z>0, DK: 0000 0000 0000 0011.
(b) Так как Z<0,
| (1) Модуль числа | 0000 0000 0000 0011 |
| (2) Инверсия числа | 1111 1111 1111 1100 |
| (3) DK | 1111 1111 1111 1101 |
Проверка:
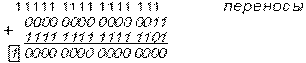
Вновь убеждаемся, что
DK(Z) + DK(–Z) = 0 (14).
Видно, что общее количество кодов совпадает и, следовательно, одинаковым будет количество кодируемых чисел в обоих способах.
Дополнительных кодов оказывается на один больше, чем прямых, и интервал целых чисел со знаком при их размещении в 2-байтном машинном слове составляет [–32768; 32767] - именно такими являются граничные значения целых чисел типа Integer в языке PASCAL, что свидетельствует об использовании дополнительного кодирования в представлении чисел.
Перевод в дополнительный код происходит автоматически при вводе чисел; в таком виде числа хранятся в ОЗУ и затем участвуют в арифметических операциях.
При этом, как уже было сказано, операция вычитания двух чисел как самостоятельная отсутствует – она заменяется сложением первого числа с дополнительным кодом второго, т.е. просто сложением содержимого двух ячеек памяти. Убедимся в правомочности этого.
Пример 15. Найти значение (27 – 3)10 в двоичной кодировке.
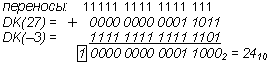
В данном случае появление 1 в регистре переполнения не интерпретируется как ошибка вычислений, поскольку на ее отсутствие указывают знаки чисел и результата.
Порядок проверок и анализа корректности операций сложения-вычитания
Z = Z(1) + Z(2)
можно представить в виде таблицы:
| Таблица 3. Проверка и анализ корректности результатов | ||||
| Старший бит | Рег. переп. | Комментарий | ||
| Z(1) | Z(2) | Z | ||
| 0 | 0 | 0 | 0 | Сложение двух положительных чисел без переполнения. Результат корректен |
| 0 | 0 | 1 | 0 | Переполнение при сложении двух положительных чисел. Результат некорректен |
| 1 | 1 | 1 | 1 | Сложение двух отрицательных чисел без переполнения. Результат корректен |
| 1 | 1 | 0 | 1 | Переполнение при сложении двух положительных чисел. Результат некорректен |
| 0 | 1 | 0 | 1 | Сложение чисел с разными знаками; Z(1)>|Z(2)|. Результат корректен |
| 0 | 1 | 1 | 0 | Сложение чисел с разными знаками; Z(1)<|Z(2)|. Результат корректен |
Необходимо уточнить, что при выполнении вычитания отрицательного числа оно из дополнительного кода переводится в прямой, и вновь вместо вычитания производится сложение.
Подобным же образом число из дополнительного кода переводится в прямой при выполнении операции умножения;
Перемножаются всегда положительные числа по рассмотренным выше правилам; знаковый бит результата, очевидно, будет содержать 0, если знаки чисел одинаковы, и 1 при противоположных знаках.
Над множеством целых чисел со знаком операция деления не определена, поскольку в общем случае ее результатом будет вещественное число.
Однако допустимыми являются операции целочисленного деления и нахождения остатка от целочисленного деления
Точнее, значения обеих величин находятся одновременно в одной процедуре, которая в конечном счете сводится к последовательности вычитаний или, еще точнее, сложений с дополнительным кодом делителя.
Примем обозначения:
· Z(1) – делимое;
· Z(2) – делитель;
· L – результат целочисленного деления Z(1) на Z(2);
· R – остаток от целочисленного деления Z(1) на Z(2).
Эти величины связаны между собой соотношением:
Z(1) = L· Z(2) + R,
из которого следует алгоритм нахождения значений L и R для заданных Z(1) и Z(2); его блок-схема для положительных Z(1) на Z(2) представлена на рисунке 1.
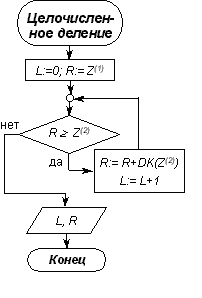 |
Рис.1. Алгоритм выполнения целочисленного деления
Таким образом, операции div и mod, как, впрочем, и операция умножения, реализуются программно, т.е. сводятся к последовательности небольшого числа более простых действий.
При этом уровень программной реализации может быть различным.
Если реализация выполнена на уровне команд центрального процессора, то эти операции оказываются доступны из любого приложения (любой прикладной программы).
Если же в системе команд процессора эти микропрограммы отсутствуют, их приходится описывать в виде процедур в самих приложениях и, следовательно, они будут доступны только в этих приложениях.








