При отсутствии помех передачи всегда возможен такой вариант кодирования сообщения, при котором избыточность кода будет сколь угодно близкой к нулю.
Данные утверждения являются теоремами и, следовательно, должны доказываться, однако доказательства мы опустим.
Для нас важно, что теорема открывает принципиальную возможность оптимального кодирования.
Однако необходимо сознавать, что из самой теоремы никоим образом не следует, как такое кодирование осуществить практически – для этого должны привлекаться какие-то дополнительные соображения.
Ограничим себя ситуацией, когда M = 2, т.е. для представления кодов в линии связи используется лишь два типа сигналов – с практической точки зрения это наиболее просто реализуемый вариант.
Например, существование напряжения в проводе (будем называть это импульсом) или его отсутствие (пауза);
наличие или отсутствие отверстия на перфокарте или намагниченной области на дискете);
Подобное кодирование называется двоичным. Знаки двоичного алфавита принято обозначать "0" и "1", но нужно воспринимать их как буквы, а не цифры.
Удобство двоичных кодов и в том, что при равных длительностях и вероятностях каждый элементарный сигнал (0 или 1) несет в себе 1 бит информации (log2M = 1);
Тогда из (1), теоремы Шеннона:
I1(A) 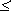 K(2)
K(2)
и первая теорема Шеннона получает следующую интерпретацию:
При отсутствии помех передачи средняя длина двоичного кода может быть сколь угодно близкой к средней информации, приходящейся на знак первичного алфавита.
Применение формулы (2) для двоичного кодирования дает:
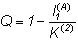
Определение количества переданной информации при двоичном кодировании сводится к простому подсчету числа импульсов (единиц) и пауз (нулей).
При этом возникает проблема выделения из потока сигналов (последовательности импульсов и пауз) отдельных кодов. Приемное устройство фиксирует интенсивность и длительность сигналов.
Элементарные сигналы (0 и 1) могут иметь одинаковые или разные длительности.
Их количество в коде (длина кодовой цепочки), который ставится в соответствие знаку первичного алфавита, также может быть одинаковым (в этом случае код называется равномерным) или разным (неравномерный код).
Наконец, коды могут строиться для каждого знака исходного алфавита (алфавитное кодирование) или для их комбинаций (кодирование блоков, слов).
В результате при кодировании (алфавитном и словесном) возможны следующие варианты сочетаний:
Таблица 1. Варианты сочетаний
| Длительности элементарных сигналов | Кодировка первичных символов (слов) | Ситуация |
| одинаковые | равномерная | (1) |
| одинаковые | неравномерная | (2) |
| разные | равномерная | (3) |
| разные | неравномерная | (4) |
В случае использования неравномерного кодирования или сигналов разной длительности (ситуации (2), (3) и (4)) для отделения кода одного знака от другого между ними необходимо передавать специальный сигнал – временной разделитель (признак конца знака) или применять такие коды, которые оказываются уникальными, т.е. несовпадающими с частями других кодов.
При равномерном кодировании одинаковыми по длительности сигналами (ситуация (1)) передачи специального разделителя не требуется, поскольку отделение одного кода от другого производится по общей длительности, которая для всех кодов оказывается одинаковой (или одинаковому числу бит при хранении).
Длительность двоичного элементарного импульса (  ) показывает, сколько времени требуется для передачи 1 бит информации.
) показывает, сколько времени требуется для передачи 1 бит информации.
Очевидно, для передачи информации, в среднем приходящейся на знак первичного алфавита, необходимо время 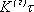 .
.
Таким образом, задачу оптимизации кодирования можно сформулировать в иных терминах:
построить такую систему кодирования, чтобы суммарная длительность кодов при передаче (или суммарное число кодов при хранении) данного сообщения была бы наименьшей.
6. Равномерное алфавитное двоичное кодирование .
6.1. Байтовый код
Двоичный код первичного алфавита строится цепочками равной длины, т.е. со всеми знаками связано одинаковое количество информации равное I0.
Передавать признак конца знака не требуется, поэтому для определения длины кодовой цепочки можно воспользоваться формулой:
K(2) 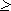 log2N.
log2N.
Приемное устройство просто отсчитывает определенное заранее количество элементарных сигналов и интерпретирует цепочку (устанавливает, какому знаку она соответствует).
Правда, при этом возможны сбои. Например, пропуск (непрочтение) одного элементарного сигнала приведет к сдвигу всей кодовой последовательности и неправильной ее интерпретации; Эта проблема решается путем синхронизации передачи или иными способами.
С другой стороны, применение равномерного кода оказывается одним из средств контроля правильности передачи, поскольку факт поступления лишнего элементарного сигнала или, наоборот, поступление неполного кода сразу интерпретируется как ошибка.
Примером использования равномерного алфавитного кодирования является
6.2. Представление символьной информации в компьютере.
Чтобы определить длину кода, необходимо начать с установления количество знаков в первичном алфавите. Компьютерный алфавит должен включать:
26 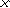 2=52 букв латинского алфавита (с учетом прописных и строчных);
2=52 букв латинского алфавита (с учетом прописных и строчных);
33 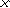 2=66 букв русского алфавита;
2=66 букв русского алфавита;
цифры 0...9 – всего 10;
знаки математических операций, знаки препинания, спецсимволы  20.
20.
Получаем, что общее число символов N  148. Теперь можно оценить длину кодовой цепочки:
148. Теперь можно оценить длину кодовой цепочки:
K(2) 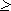 log2148
log2148 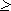 7,21.
7,21.
Поскольку K(2) должно быть целым, очевидно, K(2)= 8.
Именно такой способ кодирования принят в компьютерных системах: любому символу ставится в соответствие цепочка из 8 двоичных разрядов (8 бит).
Такая цепочка получила название байт, а представление таким образом символов – байтовым кодированием.
Байт наряду с битом может использоваться как единица измерения количества информации в сообщении.
Один байт соответствует количеству информации в одном символе алфавита при их равновероятном распределении. Этот способ измерения количества информации называется также объемным.
Пусть имеется некоторое сообщение (последовательность знаков).
Оценка количества содержащейся в нем информации согласно рассмотренному ранее вероятностному подходу (с помощью формулы Шеннона ) дает Iвер, а объемная мера пусть равна Iоб; соотношение между этими величинами:
Iвер 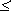 Iоб
Iоб
Именно байт принят в качестве единицы измерения количества информации в международной системе единиц СИ. 1 байт = 8 бит.
Наряду с байтом для измерения количества информации используются более крупные производные единицы:
1 Кбайт = 210 байт = 1024 байт (килобайт)
1 Мбайт = 220 байт = 1024 Кбайт (мегабайт)
1 Гбайт = 230 байт = 1024 Мбайт (гигабайт)
1 Тбайт = 240 байт = 1024 Гбайт (терабайт)
Использование 8-битных цепочек позволяет закодировать 28=256 символов, что превышает оцененное выше N и, следовательно, дает возможность употребить оставшуюся часть кодовой таблицы для представления дополнительных символов.
Однако стандартизация длины кода недостаточна, поскольку способов кодирования, т.е. вариантов сопоставления знакам первичного алфавита восьми битных цепочек, очень много.
Для обеспечения совместимости технических устройств и обеспечения возможности обмена информацией между многими потребителями требуется согласование (стандартизация) кодов, которое осуществляется в форме стандартных кодовых таблиц.
В персональных компьютерах и телекоммуникационных системах применяется международный байтовый код ASCII (American Standard Code for Information Interchange – "американский стандартный код обмена информацией").
Он регламентирует коды первой половины кодовой таблицы (номера кодов от 0 до 127, т.е. первый бит всех кодов 0).
В эту часть попадают коды прописных и строчных английских букв, цифры, знаки препинания и математических операций, а также некоторые управляющие коды (номера от 0 до 31). Ниже приведены некоторые ASCII-коды:
| Таблица 1. Некоторые ASCII-коды | ||
| Знак, клавиша | Код двоичный | Код десятичный |
| пробел | 00100000 | 32 |
| A (лат) | 01000001 | 65 |
| B (лат) | 01000010 | 66 |
| Z | 01011010 | 90 |
| 0 | 00110000 | 48 |
| 1 | 00110001 | 49 |
| 9 | 00111001 | 57 |
| Клавиша ESC | 00011011 | 27 |
Вторая часть кодовой таблицы – она считается расширением основной – охватывает коды в интервале от 128 до 255 (первый бит всех кодов 1).
Она используется для представления символов национальных алфавитов (например, русского или греческого), а также символов псевдографики.
Для этой части также имеются стандарты, например, для символов русского языка это КОИ–8, КОИ–7 и др.








