Математическая постановка задачи кодирования
На этом шаге мы рассмотрим математическую постановку задачи кодирования.
Не обсуждая технических сторон передачи и хранения сообщения (т.е. того, каким образом фактически реализованы передача-прием последовательности сигналов или фиксация состояний), попробуем дать математическую постановку задачи кодирования.
Пусть:
· первичный алфавит A содержит N знаков со средней информацией на знак, определенной с учетом вероятностей их появления, I1(A) (нижний индекс отражает то обстоятельство, что рассматривается первое приближение, а верхний индекс в скобках указывает алфавит).
· исходное сообщение, представленное в первичном алфавите, содержит n знаков
· вторичный алфавит B пусть содержит M знаков со средней информационной емкостью I1(В).
· закодированное сообщение – m знаков.
Если исходное сообщение содержит I(A) информации, а закодированное – I(B), то условие обратимости кодирования, т.е. неисчезновения информации при кодировании, очевидно, может быть записано следующим образом:
I(A) 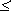 I(B),
I(B),
Смысл этого условия в том, что операция обратимого кодирования может увеличить количество формальной информации в сообщении, но не может его уменьшить.
Однако каждая из величин в данном неравенстве может быть заменена произведением числа знаков на среднюю информационную емкость знака, т.е.:

Отношение m/n характеризует среднее число знаков вторичного алфавита, которое приходится использовать для кодирования одного знака первичного алфавита – будем называть его длиной кода или длиной кодовой цепочки и обозначим
K(B)= m/n (верхний индекс указывает алфавит кодов).
В частном случае, когда появление любых знаков вторичного алфавита равновероятно, согласно формуле Хартли I1(B) =log2M, и тогда
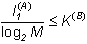 (1)
(1)
По аналогии с величиной R, характеризующей избыточность языка, можно ввести относительную избыточность кода Q:
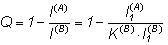 (2)
(2)
Данная величина показывает, насколько операция кодирования увеличила длину исходного сообщения.
Очевидно, чем меньше Q (т.е. чем ближе она к 0 или, что то же, I(B) ближе к I(A)), тем более выгодным оказывается код и более эффективной операция кодирования.
Выгодность кодирования при передаче и хранении – это экономический фактор, поскольку более эффективный код позволяет затратить на передачу сообщения меньше энергии, а также времени и, соответственно, меньше занимать линию связи; при хранении используется меньше площади поверхности (объема) носителя.
При этом следует сознавать, что выгодность кода не идентична временнóй выгодности всей цепочки кодирование – передача – декодирование;
Возможна ситуация, когда за использование эффективного кода при передаче придется расплачиваться тем, что операции кодирования и декодирования будут занимать больше времени и иных ресурсов (например, места в памяти технического устройства, если эти операции производятся с его помощью).
Выражение (1) пока следует воспринимать как соотношение оценочного характера, из которого неясно, в какой степени при кодировании возможно приближение к равенству его правой и левой частей.
По этой причине для теории связи важнейшее значение имеют две теоремы, доказанные Шенноном.
Первая –затрагивает ситуацию с кодированием при передаче сообщения по линии связи, в которой отсутствуют помехи, искажающие информацию. Вторая теорема относится к реальным линиям связи с помехами.
Первая теорема Шеннона, которая называется также основной теоремой о кодировании при отсутствии помех, формулируется следующим образом:
При отсутствии помех передачи всегда возможен такой вариант кодирования сообщения, при котором среднее число знаков кода, приходящихся на один знак кодируемого алфавита, будет сколь угодно близко к отношению средних информаций на знак первичного и вторичного алфавитов.
Используя понятие избыточности кода, можно дать более короткую формулировку теоремы:








