Таким образом: за меру неопределенности опыта с n равновероятными исходами можно принять число logа(n).
Выбор основания логарифма в данном случае значения не имеет, поскольку в силу известной формулы
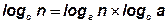
преобразования логарифма logа(n) от одного основания а к другому основанию с состоит во введении одинакового для обеих частей выражения (1.1) постоянного множителя logca, что равносильно изменению масштаба (т.е. размера единицы) измерения неопределенности.
Исходя из этого, мы имеет возможность выбрать из каких-то дополнительных соображений основание логарифма.
Таким удобным основанием оказывается 2, поскольку в этом случае за единицу измерения принимается неопределенность, содержащаяся в опыте, имеющем лишь два равновероятных исхода, которые можно обозначить, например, ИСТИНА (True) и ЛОЖЬ (False) и использовать для анализа таких событий аппарат математической логики.
Единица измерения неопределенности при двух возможных равновероятных исходах опыта называется бит
(Название бит происходит от английского binary digit, что в дословном переводе означает "двоичный разряд" или "двоичная единица".)
Таким образом, функция, описывающей меру неопределенности опыта, имеющего n равновероятных исходов, может быть представлена в виде:
f(n) = log2n (1.2).
Эта величина получила название энтропии. В дальнейшем будем обозначать ее H.
Вновь рассмотрим опыт с n равновероятными исходами.
Поскольку каждый исход случаен, он вносит свой вклад в неопределенность всего опыта, но так как все n исходов равнозначны, разумно допустить, что и их неопределенности одинаковы.
Из свойства аддитивности неопределенности (1.1), а также того, что согласно (1.2) общая неопределенность равна log2n, следует, что неопределенность, вносимая одним исходом составляет
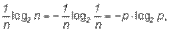
где
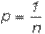
– вероятность любого из отдельных исходов.
Таким образом, неопределенность, вносимая каждым из равновероятных исходов, равна:
H = - p log2p (1.3).
Обобщим формулу (1.3) на ситуацию, когда исходы опытов не равновероятны, например, p(A1) и p(A2).
Тогда:
H1 = - p(A1) log2 p(A1) и H2 = - p(A2) log2 p(A2)
H = H1 + H2 = -p(A1) log2 p(A1) - p(A2) log2 p(A2)
Обобщая это выражение на ситуацию, когда опыт  имеет n не равновероятных исходов A1, A2,..., An, получим:
имеет n не равновероятных исходов A1, A2,..., An, получим:
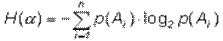 (1.4)
(1.4)
Введенная таким образом величина, как уже было сказано, называется энтропией опыта  .
.
Используя формулу для среднего значения дискретных случайных величин, можно записать:
H(  ) = - log2 p (
) = - log2 p ( 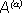 ),
),
где 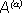 – обозначает исходы, возможные в опыте
– обозначает исходы, возможные в опыте  .
.
Энтропия является мерой неопределенности опыта, в котором проявляются случайные события, и равна средней неопределенности всех возможных его исходов.
Для практики формула (1.4) важна тем, что позволяет сравнить неопределенности различных опытов со случайными исходами.
Пример. Имеются два ящика, в каждом из которых по 12 шаров.
- в первом – 3 белых, 3 черных и 6 красных;
- во втором – каждого цвета по 4.
Опыты состоят в вытаскивании по одному шару из каждого ящика.
Что можно сказать относительно неопределенностей исходов этих опытов?
Согласно (1.4) находим энтропии обоих опытов:
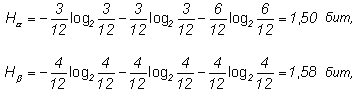
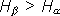 , т.е. неопределенность результата в опыте
, т.е. неопределенность результата в опыте  выше и, следовательно, предсказать его можно с меньшей долей уверенности, чем результат
выше и, следовательно, предсказать его можно с меньшей долей уверенности, чем результат  .
.
2.3. Свойства энтропии
1. Как следует из (1.4), H = 0 только в двух случаях:
· Какая-либо из вероятностей p(Aj) = 1;
Однако, при этом следует, что все остальные p(Ai) = 0 (i 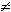 j), т.е. реализуется ситуация, когда один из исходов является достоверным (и общий итог опыта перестает быть случайным);
j), т.е. реализуется ситуация, когда один из исходов является достоверным (и общий итог опыта перестает быть случайным);
· Все вероятности p(Ai) = 0,
То есть никакие из рассматриваемых исходов опыта невозможны, поскольку нетрудно показать, что 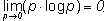
Во всех остальных случаях, очевидно, что H > 0.
2. Очевидным следствием свойства аддитивности (1.1) будет утверждение, что для двух независимых опытов  и
и 
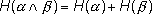 (1.5)
(1.5)
Энтропия сложного опыта, состоящего из нескольких независимых, равна сумме энтропий отдельных опытов.
3. Пусть имеется два опыта с одинаковым числом исходов n, но в одном случае они равновероятны, а в другом – нет. Каково соотношение энтропий опытов?
Примем без доказательства следующее утверждение:
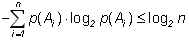 (1.7)
(1.7)
То есть при прочих равных условиях наибольшую энтропию имеет опыт с равновероятными исходами. Другими словами, энтропия максимальна в опытах, где все исходы равновероятны.
2.4. Понятие условной энтропии
Найдем энтропию сложного опыта 
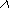
 в том случае, если опыты не являются независимыми, т.е. если на исход
в том случае, если опыты не являются независимыми, т.е. если на исход  оказывает влияние результат опыта
оказывает влияние результат опыта  .
.
Например, если в ящике всего два разноцветных шара и  состоит в извлечении первого, а
состоит в извлечении первого, а  – второго из них, то
– второго из них, то  полностью снимает неопределенность сложного опыта
полностью снимает неопределенность сложного опыта 
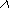
 , т.е. оказывается
, т.е. оказывается
H( 
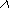
 ) = H(
) = H(  ),
),
а не сумме энтропии, как следует из (1.5).
Связь между  на
на 
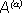 могут оказывать влияние на исходы из
могут оказывать влияние на исходы из 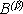 , т.е. некоторые пары событий Ai
, т.е. некоторые пары событий Ai 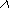 Bj не являются независимыми.
Bj не являются независимыми.
Доказано, что для энтропии сложного опыта справедливо соотношение:
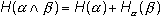 ,(1.10)
,(1.10)
где 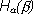 есть средняя условная энтропия опыта
есть средняя условная энтропия опыта  при условии выполнении опыта
при условии выполнении опыта  .
.
Полученное выражение представляет собой общее правило нахождения энтропии сложного опыта. При этом выражение (1.5) является частным случаем (1.10) при условии независимости опытов  и
и  .
.
Относительно условной энтропии можно высказать следующие утверждения:
1. Условная энтропия является величиной неотрицательной.
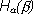 = 0 только в том случае, если любой исход
= 0 только в том случае, если любой исход  полностью определяет исход
полностью определяет исход  (как в примере с двумя шарами), т.е.
(как в примере с двумя шарами), т.е. 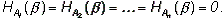 В этом случае H (
В этом случае H ( 
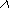
 ) = H (
) = H (  ).
).
2. Если опыты  и
и  независимы, то
независимы, то 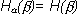 , причем это оказывается наибольшим значением условной энтропии. Другими словами, опыт
, причем это оказывается наибольшим значением условной энтропии. Другими словами, опыт  не может повысить неопределенность опыта
не может повысить неопределенность опыта  ; он может либо не оказать никакого влияния (если опыты независимы), либо понизить энтропию
; он может либо не оказать никакого влияния (если опыты независимы), либо понизить энтропию  .
.
Приведенные утверждения можно объединить одним неравенством:
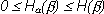 (1.11)
(1.11)
т.е. условная энтропия не превосходит безусловную.
Из соотношений (1.10) и (1.11) следует, что
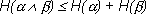 (1.12)
(1.12)
причем равенство реализуется только в том случае, если опыты  и
и  независимы.
независимы.
3. СВЯЗЬ МЕЖДУ ЭНТРОПИЕЙ И ИНФОРМАЦИЕЙ
Рассмотрим пример.
В ящике имеются 2 белых шара и 4 черных.
Из ящика извлекают последовательно два шара без возврата.
Найти энтропию, связанную с первым и вторым извлечениями, а также энтропию обоих извлечений.
Будем считать опытом  извлечение первого шара.
извлечение первого шара.
Он имеет два исхода:
· A1 – вынут белый шар; его вероятность p(A1) = 2/6 = 1/3;
· A2 – вынут черный шар; его вероятность p(A2)=1 – p(A1) = 2/3.
Эти данные позволяют с помощью (1.4) сразу найти H(  ):
):
H(  )= – p(A1)log2 p(A1) – p(A2)log2 p(A2) = –1/3 log21/3 – 2/3 log22/3 = 0,918 бит
)= – p(A1)log2 p(A1) – p(A2)log2 p(A2) = –1/3 log21/3 – 2/3 log22/3 = 0,918 бит
Опыт  – извлечение второго шара также имеет два исхода:
– извлечение второго шара также имеет два исхода:
· B1 – вынут белый шар;
· B2 – вынут черный шар,
Однако их вероятности будут зависеть от того, каким был исход опыта  .
.
В частности:
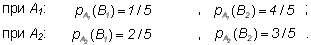
Следовательно, энтропия, связанная со вторым опытом, является условной и, согласно (1.8) и (1.9), равна:
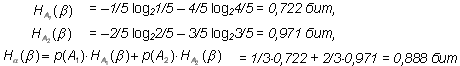
Наконец, из (1.10): H( 
 ) = 0,918 + 0,888 = 1,806 бит.
) = 0,918 + 0,888 = 1,806 бит.
Из рассмотренного примера видно как предшествующий опыт (  ) может уменьшить количество исходов и, следовательно, неопределенность последующего опыта (
) может уменьшить количество исходов и, следовательно, неопределенность последующего опыта (  ).
).
Разность H(  ) и
) и 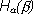 , очевидно, показывает, какие новые сведения относительно
, очевидно, показывает, какие новые сведения относительно  мы получаем, произведя опыт
мы получаем, произведя опыт  . Эта величина называется информацией относительно опыта
. Эта величина называется информацией относительно опыта  , содержащейся в опыте
, содержащейся в опыте  .
.
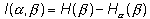 (1.13)
(1.13)
Данное выражение открывает возможность численного измерения количества информации, поскольку оценивать энтропию мы уже умеем.
Из него легко получить ряд следствий.
Следствие 1. Поскольку единицей измерения энтропии является бит, то в этих же единицах может быть измерено количество информации.
Следствие 2. Пусть опыт  =
=  , т.е. просто произведен опыт
, т.е. просто произведен опыт  . Поскольку он несет полную информацию о себе самом, неопределенность его исхода полностью снимается, т.е.
. Поскольку он несет полную информацию о себе самом, неопределенность его исхода полностью снимается, т.е. 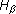
 =0.
=0.
Тогда I(  ,
,  ) = H (
) = H (  ), т.е. можно считать, что энтропия равна информации относительно опыта, которая содержится в нем самом.
), т.е. можно считать, что энтропия равна информации относительно опыта, которая содержится в нем самом.
Можно построить уточнение: энтропия опыта равна той информации, которую мы получаем в результате его осуществления.
Отметим ряд свойств информации.
I(  ,
,  )
) 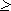 0, причем I(
0, причем I(  ,
,  ) = 0 тогда и только тогда, когда опыты
) = 0 тогда и только тогда, когда опыты  и
и  независимы. Это свойство непосредственно вытекает из (1.10) и (1.13).
независимы. Это свойство непосредственно вытекает из (1.10) и (1.13).
I(  ,
,  ) = I(
) = I(  ,
,  ), т.е. информация симметрична относительно последовательности опытов.
), т.е. информация симметрична относительно последовательности опытов.
Следствие 2 и представление энтропии в виде (1.4) позволяют записать:
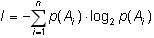 (1.14)
(1.14)
т.е. информация опыта равна среднему значению количества информации, содержащейся в каком-либо одном его исходе.
Рассмотрим ряд примеров применения формулы (1.14).
Пример 1. Какое количество информации требуется, чтобы узнать исход броска монеты? В данном случае n=2 и события равновероятны, т.е. p1=p2=0,5. Согласно (1.14):
I = – 0,5•log20,5 – 0,5•log20,5 = 1 бит
Пример 2. Игра "Угадайка – 4". Некто задумал целое число в интервале от 0 до 3. Наш опыт состоит в угадывании этого числа. На наши вопросы Некто может отвечать лишь "Да" или "Нет". Какое количество информации мы должны получить, чтобы узнать задуманное число, т.е. полностью снять начальную неопределенность? Как правильно построить процесс угадывания?
Исходами в данном случае являются: A1 – "задуман 0", A2 – "задумана 1", A3 – "задумана 2", A4 – "задумана 3".
Конечно, предполагается, что вероятности быть задуманными у всех чисел одинаковы. Поскольку n = 4, следовательно, p(Ai)=1/4, log2 p(Ai) = –2 и I = 2 бит. Таким образом, для полного снятия неопределенности опыта (угадывания задуманного числа) нам необходимо 2 бита информации.
Теперь выясним, какие вопросы необходимо задать, чтобы процесс угадывания был оптимальным, т.е. содержал минимальное их число.
Здесь удобно воспользоваться так называемым выборочным каскадом:
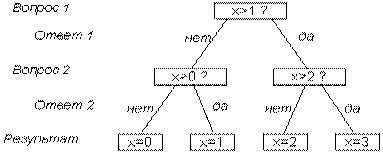
Таким образом, для решения задачи оказалось достаточно 2-х вопросов независимо от того, какое число было задумано. Совпадение между количеством информации и числом вопросов с бинарными ответами неслучайно.
Количество информации численно равно числу вопросов с равновероятными бинарными вариантами ответов, которые необходимо задать, чтобы полностью снять неопределенность задачи.
В рассмотренном примере два полученных ответа в выборочном каскаде полностью сняли начальную неопределенность.
Подобная процедура позволяет определить количество информации в любой задаче, интерпретация которой может быть сведена к парному выбору.
В такой процедуре все n исходов равновероятны. В этом случае для формулы (1.14) все

I = log2n (1.15)
Эта формула была выведена в 1928 г. американским инженером Р.Хартли и носит его имя. Она связывает количество равновероятных состояний (n) и количество информации в сообщении (I), о том, что любое из этих состояний реализовалось.
Смысл этой формулы в том, что, если некоторое множество содержит n элементов и x принадлежит данному множеству, то для его выделения (однозначной идентификации) среди прочих требуется количество информации, равное log2n.
Частным случаем применения формулы (1.15) является ситуация, когда n=2k; подставляя это значение в (1.15), очевидно, получим:
I = k бит (1.16)
Таким образом, величина k равна количеству вопросов с бинарными равновероятными ответами, которые определяли количество информации в задачах, решаемых методом парного выбора
Пример 3. Случайным образом вынимается карта из колоды в 32 карты. Какое количество информации требуется, чтобы угадать, что это за карта? Как построить угадывание?
Для данной задачи n = 25, значит, k = 5 и, следовательно, I = 5 бит. Последовательность вопросов придумайте самостоятельно.
Выражение (1.13) интерпретировать следующим образом: если начальная энтропия опыта H1, а в результате сообщения информации I энтропия становится равной H2 (очевидно, H1 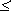 H2), то
H2), то
I = H1 – H2,
т.е. информация равна убыли энтропии.
В частном случае, если изначально равновероятных исходов было n1, а в результате передачи информации I неопределенность уменьшилась, и число исходов стало n2 (очевидно, n2 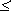 n1), то из (1.15) легко получить:
n1), то из (1.15) легко получить:
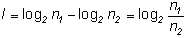
Таким образом, можно дать следующее определение:
Информация – это содержание сообщения, понижающего неопределенность некоторого опыта с неоднозначным исходом. Убыль связанной с ним энтропии является количественной мерой информации.
В случае равновероятных исходов информация равна логарифму отношения числа возможных исходов до и после (получения сообщения).
4. Объективность информации.
При использовании людьми одна и та же информация может иметь различную оценку с точки зрения значимости (важности, ценности).
Определяющим в такой оценке оказывается содержание (смысл) сообщения для конкретного потребителя.
Однако при решении практических задач технического характера содержание сообщения может не играть роли.
Например, задача телеграфной (и любой другой) линии связи является точная и безошибочная передача сообщения без анализа того, насколько ценной для получателя оказывается связанная с ним информация.
Техническое устройство не может оценить важности информации – его задача без потерь передать или сохранить информацию.
Выше мы определили информацию как результат выбора. Такое определение не зависит от того, кто и каким образом осуществляет выбор, а связанная с ним количественная мера информации – одинаковой для любого потребителя.
Следовательно, появляется возможность объективного измерения информации, при этом результат измерения – абсолютен.
Это служит предпосылкой для решения технических задач. Нельзя предложить абсолютной и единой для всех меры ценности информации.
С точки зрения формальной информации страница из учебника информатики или из романа "Война и мир" и страница, записанная бессмысленными значками, содержат одинаковое количество информации.
Количественная сторона информации объективна, смысловая – нет. Однако, жертвуя смысловой (семантической) стороной информации, мы получаем объективные методы измерения ее количества, а также обретаем возможность описывать информационные процессы математическими уравнениями.
Это является условием применимости законов теории информации к анализу и описанию информационных процессов.
5. Информация и алфавит
Естественной для органов чувств человека является аналоговая форма представления информации, универсальной признано считать дискретную форму представления информации с помощью некоторого конечного набора знаков – алфавита.
Именно таким образом представленная информация обрабатывается компьютером, передается по компьютерным и иным линиям связи.
Сообщение есть последовательность знаков алфавита. При их передаче возникает проблема распознавания знака: каким образом прочитать сообщение, т.е. по полученным сигналам установить исходную последовательность знаков первичного алфавита.
В устной речи это достигается использованием различных фонем (основных звуков разного звучания), по которым мы и отличает знаки речи.
В письменности это достигается различным начертанием букв и дальнейшим нашим анализом написанного.
Появление конкретного знака (буквы) в конкретном месте сообщения – событие случайное. Следовательно, узнавание (отождествление) знака требует получения некоторой порции информации.
Можно связать эту информацию с самим знаком и считать, что знак несет в себе (содержит) некоторое количество информации. Оценим это количество.
Самое грубое приближение – нулевое (номер приближения отражается индексом у получаемых величин).
Предположим, что появление всех знаков (букв) алфавита в сообщении равновероятно.
Тогда количество знаков для английского алфавита - ne=27 (с учетом пробела как самостоятельного знака); для русского алфавита - nr=34. Из формулы Хартли находим:
I0(e) =log227 = 4,755 бит.
I0(r) =log234 = 5,087 бит.
Получается, что в нулевом приближении со знаком русского алфавита в среднем связано больше информации, чем со знаком английского.
Например, в русской букве "а" информации больше, чем в "a" английской!
Это, безусловно, не означает, что английский язык – язык Шекспира и Диккенса – беднее, чем язык Пушкина и Достоевского.
Лингвистическое богатство языка определяется количеством слов и их сочетаний, а это никак не связано с числом букв в алфавите.
С точки зрения техники это означает, что сообщения из равного количества символов будет иметь разную длину (и соответственно, время передачи) и большими они окажутся у сообщений на русском языке.
В качестве следующего (первого) приближения, уточняющего исходное, попробуем учесть то обстоятельство, что относительная частота, т.е. вероятность появления различных букв в сообщении различна.
Рассмотрим таблицу средних частот букв для русского алфавита, в который включен также знак "пробел" для разделения слов (из книги А.М. и И.М.Ягломов [с.238]);
с учетом неразличимости букв "е" и "ë", а также "ь" и "ъ" (так принято в телеграфном кодировании), получим алфавит из 32 знаков со следующими вероятностями их появления в русских текстах:
| Таблица 1. Частота появления букв Буква | Частота | Буква | Частота | Буква | Частота | Буква | Частота |
| пробел | 0,175 | o | 0,090 | е, ë | 0,072 | а | 0,062 |
| и | 0,062 | т | 0,053 | н | 0,053 | с | 0,045 |
| р | 0,040 | в | 0,038 | л | 0,035 | к | 0,028 |
| м | 0,026 | д | 0,025 | п | 0,023 | у | 0,021 |
| я | 0,018 | ы | 0,016 | з | 0,016 | ъ, ь | 0,014 |
| б | 0,014 | г | 0,013 | ч | 0,012 | й | 0,010 |
| х | 0,009 | ж | 0,007 | ю | 0,006 | ш | 0,006 |
| ц | 0,004 | щ | 0,003 | э | 0,003 | ф | 0,003 |
Для оценки информации, связанной с выбором одного знака алфавита с учетом неравной вероятности их появления в сообщении (текстах) можно воспользоваться формулой (1.14).
Из нее, в частности, следует, что если pi – вероятность (относительная частота) знака номер i данного алфавита из N знаков, то среднее количество информации, приходящейся на один знак, равно:
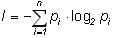 (1.17)
(1.17)
Это и есть знаменитая формула К.Шеннона, с работы которого "Математическая теория связи" (1948) принято начинать отсчет возраста информатики, как самостоятельной науки.
В нашей стране практически одновременно с Шенноном велись подобные исследования, например, и в том же 1948 г. вышла работа А.Н.Колмогорова "Математическая теория передачи информации".
Применение формулы (1.17) к различным алфавитам дает следующие значение средней информации на знак:
· алфавиту русского языка дает 1(r)= 4,36 бит,
· а для английского языка I1(e) = 4,04 бит,
· для французского I1(l) = 3,96 бит,
· для немецкого I1(d) = 4,10 бит,
· для испанского I1(s) = 3,98 бит.
Как мы видим, и для русского, и для английского языков учет вероятностей появления букв в сообщениях приводит к уменьшению среднего информационного содержания буквы, что, кстати, подтверждает справедливость формулы (1.7).
Несовпадение значений средней информации для английского, французского и немецкого языков, основанных на одном алфавите, связано с тем, что частоты появления одинаковых букв в них различаются.
В рассматриваемом приближении по умолчанию предполагается, что вероятность появления любого знака в любом месте сообщения остается одинаковой и не зависит от того, какие знаки или их сочетания предшествуют данному.
Такие сообщения называются шенноновскими (или сообщениями без памяти).
Сообщения, в которых вероятность появления каждого отдельного знака не меняется со временем, называются шенноновскими, а порождающий их отправитель – шенноновским источником.
Если сообщение является шенноновским, то набор знаков (алфавит) и вероятности их появления в сообщении могут считаться известными заранее.
В этом случае:
· с одной стороны, можно предложить оптимальные способы кодирования, уменьшающие суммарную длину сообщения при передаче по каналу связи.
· с другой стороны, интерпретация сообщения, представляющего собой последовательность сигналов, сводится к задаче распознавания знака, т.е. выявлению, какой именно знак находится в данном месте сообщения.
А такая задача, как мы уже убедились в предыдущем шаге, может быть решена серией парных выборов.
При этом количество информации, содержащееся в знаке, служит мерой затрат по его выявлению.
Последующие (второе и далее) приближения при оценке значения информации, приходящейся на знак алфавита, строятся путем учета корреляций, т.е. связей между буквами в словах.
Дело в том, что в словах буквы появляются не в любых сочетаниях; это понижает неопределенность угадывания следующей буквы после нескольких, например, в русском языке нет слов, в которых встречается сочетание щц или фъ.
И напротив, после некоторых сочетаний можно с большей определенностью, чем чистый случай, судить о появлении следующей буквы, например, после распространенного сочетания пр- всегда следует гласная буква, а их в русском языке 10 и, следовательно, вероятность угадывания следующей буквы 1/10, а не 1/33.
В связи с этим примем следующее определение:
Сообщения (а также источники, их порождающие), в которых существуют статистические связи (корреляции) между знаками или их сочетаниями, называются сообщениями (источниками) с памятью или марковскими сообщениями (источниками).
Как указывается в книге Л.Бриллюэна [с.46], учет в английских словах двухбуквенных сочетаний понижает среднюю информацию на знак до значения I2(e)=3,32 бит, учет трехбуквенных – до I3(e)=3,10 бит. Шеннон сумел приблизительно оценить I5(e)  2,1 бит, I8(e)
2,1 бит, I8(e)  1,9 бит. Аналогичные исследования для русского языка дают: I2(r) = 3,52 бит; I3(r)= 3,01 бит.
1,9 бит. Аналогичные исследования для русского языка дают: I2(r) = 3,52 бит; I3(r)= 3,01 бит.
Последовательность I0, I1, I2... является убывающей в любом языке.
Экстраполируя ее на учет бесконечного числа корреляций, можно оценить предельную информацию на знак в данном языке 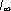 , которая будет отражать минимальную неопределенность, связанную с выбором знака алфавита без учета семантических особенностей языка, в то время как I0 является другим предельным случаем, поскольку характеризует наибольшую информацию, которая может содержаться в знаке данного алфавита.
, которая будет отражать минимальную неопределенность, связанную с выбором знака алфавита без учета семантических особенностей языка, в то время как I0 является другим предельным случаем, поскольку характеризует наибольшую информацию, которая может содержаться в знаке данного алфавита.
Шеннон ввел величину, которую назвал относительной избыточностью языка:
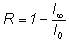 (1.18)
(1.18)
Избыточность является мерой бесполезно совершаемых альтернативных выборов при чтении текста. Эта величина показывает, какую долю лишней информации содержат тексты данного языка; лишней в том отношении, что она определяется структурой самого языка и, следовательно, может быть восстановлена без явного указания в буквенном виде.
Исследования Шеннона для английского языка дали значение 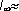 1,4÷1,5 бит, что по отношению к I0=4,755 бит создает избыточность около 0,68.
1,4÷1,5 бит, что по отношению к I0=4,755 бит создает избыточность около 0,68.
Подобные оценки показывают, что и для других европейских языков, в том числе русского, избыточность составляет 60 – 70%.
Это означает, что в принципе возможно почти трехкратное (!) сокращение текстов без ущерба для их содержательной стороны и выразительности.
Например, телеграфные тексты делаются короче за счет отбрасывания союзов и предлогов без ущерба для смысла; в них же используются однозначно интерпретируемые сокращения "ЗПТ" и "ТЧК" вместо полных слов (эти сокращения приходится использовать, поскольку знаки "." и "," не входят в телеграфный алфавит).
Однако такое "экономичное" представление слов снижает разборчивость языка, уменьшает возможность понимания речи при наличии шума (а это одна из проблем передачи информации по реальным линиям связи), а также исключает возможность локализации и исправления ошибки (написания или передачи) при ее возникновении.
Именно избыточность языка позволяет легко восстановить текст, даже если он содержит большое число ошибок или неполон (например, при отгадывании кроссвордов или при игре в "Поле чудес"). В этом смысле избыточность есть определенная страховка и гарантия разборчивости.
На практике учет корреляций в сочетаниях знаков сообщения весьма затруднителен, поскольку требует объемных статистических исследований текстов.
Кроме того, корреляционные вероятности зависят от характера текстов и целого ряда иных их особенностей.
| Таблица 1. Частота появления букв Буква | Частота | Буква | Частота | Буква | Частота | Буква | Частота |
| пробел | 0,175 | o | 0,090 | е, ë | 0,072 | а | 0,062 |
| и | 0,062 | т | 0,053 | н | 0,053 | с | 0,045 |
| р | 0,040 | в | 0,038 | л | 0,035 | к | 0,028 |
| м | 0,026 | д | 0,025 | п | 0,023 | у | 0,021 |
| я | 0,018 | ы | 0,016 | з | 0,016 | ъ, ь | 0,014 |
| б | 0,014 | г | 0,013 | ч | 0,012 | й | 0,010 |
| х | 0,009 | ж | 0,007 | ю | 0,006 | ш | 0,006 |
| ц | 0,004 | щ | 0,003 | э | 0,003 | ф | 0,00 |
По этим причинам в дальнейшем мы ограничим себя рассмотрением только шенноновских сообщений, т.е. будем учитывать различную (априорную) вероятность появления знаков в тексте, но не их корреляции.
Со следующего шага мы начнем рассматривать теорию кодирования.








