2. Энтропия как мера неопределенности
2.1. Степень неопределенности
Описать случайные события можно не только в терминах вероятностей.
То, что событие случайно, означает отсутствие полной уверенности в его наступлении, что, в свою очередь, создает неопределенность в исходах опытов, связанных с данным событием.
Степень неопределенности различна для разных ситуаций.
Например, если опыт состоит в определении возраста случайно выбранного студента 1-го курса дневного отделения вуза, то с большой долей уверенности можно утверждать, что он окажется менее 30 лет;
Гораздо меньшую определенность имеет аналогичный опыт, если проверяется, будет ли возраст произвольно выбранного студента меньше 18 лет.
Для практики важно иметь возможность произвести численную оценку неопределенности разных опытов.
2.2. Количественная мера неопределенности.
Пусть опыт имеет n равновероятных исходов.
Очевидно, что неопределенность каждого из них зависит от n, т.е. мера неопределенности является функцией числа исходов f(n).
Можно указать некоторые свойства этой функции:
1. f(1) = 0, поскольку при n = 1 исход опыта не является случайным и, следовательно, неопределенность отсутствует;
2. f(n) возрастает с ростом n, поскольку чем больше число возможных исходов, тем более затруднительным становится предсказание результата опыта.
Для определения явного вида функции f(n) рассмотрим два независимых опыта 
и 
с количествами равновероятных исходов, соответственно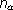 
, 
.
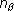(Для обозначения опытов со случайными исходами будем использовать греческие буквы , и т.д., а для обозначения отдельных исходов опытов (событий) – латинские заглавные A, B и т.д.)
Пусть имеет место сложный опыт, который состоит в одновременном выполнении опытов и ;
Число возможных его исходов равно 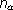· 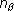, причем, все они равновероятны.
Очевидно, неопределенность исхода такого сложного опыта 
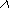
будет больше неопределенности опыта , поскольку к ней добавляется неопределенность ; мера неопределенности сложного опыта равна f( · ).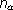
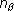С другой стороны, меры неопределенности отдельных и составляют, соответственно, f( 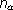) и f( ).
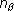В первом случае (сложный опыт) проявляется общая (суммарная) неопределенность совместных событий, во втором – неопределенность каждого из событий в отдельности.
Однако из независимости и следует, что в сложном опыте они никак не могут повлиять друг на друга и, в частности, не может оказать воздействия на неопределенность , и наоборот.
Следовательно, мера суммарной неопределенности должна быть равна сумме мер неопределенности каждого из опытов, т.е. мера неопределенности аддитивна:
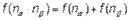(1.1)
Доказано, что единственная функция f(n), из всех существующих классов функций удовлетворяющая свойствам (1) и (2) и соотношению (1.1) является log(n).