12. Кристаллизация и формирование обычных и наплавляемых слитков

Дата: 2025-05-01; Просмотры: 4

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

104. Связь между глубиной жидкой ванны
и скоростью плавки при переплавных процессах

Задача. Определить массовую скорость плавки при ВДП сплава ХН55ВМТФКЮР в кристаллизаторе диаметром 160 мм, при которой глубина жидкой ванны равна диаметру слитка.

Исходные данные. 1. Глубину ванны считать по изоликвидусу (изотерме ликвидуса). 2. Т_лик = 1653 К; Т_сол = 1533 К. 3. Коэффициент теплопроводности l = 28,8 Вт/(м×К). 4. Удельная массовая теплоемкость C = 737 Дж/(кг×К). 5. Скрытая удельная теплота кристаллизации S = 274 кДж/кг. 6. Средний перегрев поверхности ванны DT = 100 К.

Теория. Зависимость глубины конической части жидкой ванны от массовой скорости плавки в наплавляемом слитке по данным М. Мусатова имеет вид

Н = 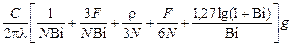, (12.1)

где Н - глубина конической части ванны; g - массовая скорость плавки;

N = 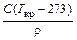; F = 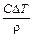; Bi = ;

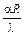Т_кр - температура кристаллизации. При Т_кр = Т_сол формула (12.1) дает значение Н для фронта солидуса, при Т_кр = Т_лик - для фронта ликвидуса; DT - перегрев металла над температурой ликвидуса; a - коэффициент теплоотдачи от слитка к кристаллизатору.

Коэффициент a зависит от температуры поверхности слитка. Поскольку эта величина слитка зависит от условий теплообмена, коэффициент a в свою очередь оказывается функцией критерия Био. С учетом этого приближенно для участка слитка, соответствующего глубине жидкой ванны, можно считать (по данным автора)

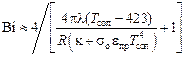, (12.2)

где R - радиус слитка; s_о - постоянная Стефана – Больцмана, 5,67×10^-8 Вт/(м²×К⁴,); e_пр - приведенная степень черноты в системе «слиток–кристаллизатор», e_пр = 0,56; k = 1260(1843 - T_сол), Вт/м².

Решение. k = 1260(1843 - 1533) = 3,9×10⁵ Вт/м²;

Bi = 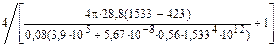= 0,408;

N = 737(1653 - 273)/(274×10³) = 3,710;

F = (737×100)/(274×10³) = 0,270;

H =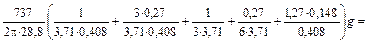
= 7,15g, м.

Отсюда необходимая массовая скорость плавки составит

g = H/7,15 = 0,16/7,15 = 0,0224 кг/с = 22,4 г/с = 1,34 кг/мин.

105. Продолжительность полного
затвердевания стального слитка

Задача. Определить продолжительность полного затвердевания слитка стали Р18 круглого сечения массой 100 кг. Масса головной части слитка 16 кг.

Исходные данные. 1. Отношение высоты тела слитка к среднему диаметру H/D_ср = 3,0. 2. Изложница расширена кверху с конусностью 6 %. Донная часть слитка имеет форму полусферы. 3. Плотность жидкой стали r = 7650 кг/м³. 4. Скрытая удельная теплота кристаллизации 245 кДж/кг. 5. Удельная массовая теплоемкость
565 Дж/(кг×К). 6. Температурный интервал кристаллизации 160 К. Перегрев над температурой ликвидуса 100 К. 7. Коэффициент теплопроводности 30 Вт/(м×К). 8. Средний перепад температуры между поверхностью слитка и стенкой изложницы 275 К. 9. Критерий Био равен 0,74.

Теория. Обычно для определения толщины корочки затвердевшего металла слитка (x) пользуются так называемой формулой квадратного корня

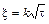, (12.3)

где t - время; k - коэффициент, зависящий от теплофизических свойств металла и условий охлаждения слитка.

Значение коэффициента k колеблются в пределах 2,2×10^-3–3,62×10^-3 м/с^0,5. Чем больше степень легирования стали, тем меньше значение k.

Хотя формула (12.3) выведена для плоских слитков, она может быть использована для определения полного времени затвердевания слитка (t_о) с любой (квадратной, круглой) формой сечения.

Для круглого слитка t = t_о при x = R, где R - радиус слитка. Отсюда по данным [3]:

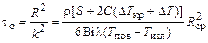, (12.4)

где r - плотность жидкого металла; S - скрытая удельная теплота кристаллизации; С - удельная массовая теплоемкость жидкого металла; l - коэффициент теплопроводности; Bi - критерий Био; DT_кр - температурный интервал кристаллизации; T_пов , T_изл - соответственно температура боковой поверхности слитка и внутренней поверхности изложницы; DT - перегрев металла над температурой ликвидуса; R - средний радиус слитка.

При сравнительно небольшой конусности, имеющей место в слитках, объем усеченного конуса примерно равен

V = (pH/2)(R² + r²), (12.5)

где R и r - соответственно радиусы верхнего и нижнего оснований.

С учетом полусферической донной части объем тела слитка составляет

V_т = (pH/2)(R² + r²) + (2p/3)r³. (12.6)

Конусность слитка определяется по формуле:

K = [(R - r)/H ]×100 %.

Величину отношения H/D_ср , равную H/(R + r), обозначим a. Средний радиус слитка связан с малым радиусом соотношением

R_сp = r/(1 - n), где n = aK/100.

Отсюда

K_сp = 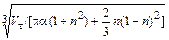. (12.7)

В свою очередь

V_т = M_т/r = (M_сл – M_г)/r, (12.8)

где M_т - масса тела слитка; M_сл - общая масса слитка; M_г - масса головной части слитка.

Решение. Объем тела слитка V_т = (100 - 16)/7650 = 1,1×10^-2 м³. Коэффициент п = (aK )/100 = (3×6)/100 = 0,18.

Средний радиус слитка

R_сp = 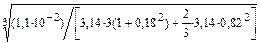= 0,10 м.

Продолжительность полного затвердевания

t_o = 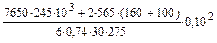= 1140 c = 19,0 мин.

106. Связь между расположением структурных зон в наплавляемом слитке и режимом переплава

Задача. Определить максимально допустимый ток переплава при ВДП хромоникелевого сплава, при котором в слитке диаметром 400 мм отсутствует зона равноосных кристаллов.

Исходные данные. 1. При переплаве на токе 18 кА ширина зоны равноосных кристаллов составляет 0,60 от диаметра слитка. 2. Глубина конической части ванны (Н_к) линейно зависит от тока I:

Н_к = 0,04(I – 2) м,

где I выражен в килоамперах.

Теория. В слитках переход от одной структурной зоны к другой, в частности, от зоны столбчатых кристаллов к зоне равноосных кристаллов определяется для металла данного состава условием

G_лик /υ_п = A, (12.9)

где G_лик - температурный градиент в некоторой точке на фронте ликвидуса; υ_п - линейная скорость продвижения фронта кристаллизации в той же точке; А - константа, характерная для данного сплава.

Для наплавляемых слитков при установившемся режиме наплавления это условие после соответствующих преобразований имеет вид

1 + (у' )²/ 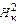= А, (12.10)

где у' - производная от кривой профиля жидкой ванны по радиусу в точке, в которой происходит смена зон; Н - глубина конической части ванны.

Если уравнение профиля жидкой ванны описывается параболой вида

у/Н_k = (r/R)²,

то у' = dy/dr = (2Н_k /R)×(r/R) и уравнение (12.10) принимает вид

(1/ 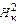) + (4/R²) 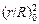= A, (12.11)

где (r/R)₀ - безразмерная ширина зоны равноосных кристаллов; R - радиус слитка.

В случае отсутствия зоны равноосных кристаллов

(r/R)₀ = 0,

что соответствует условию

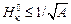, (12.12)

где 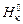- глубина конической части ванны в условиях отсутствия зоны равноосных кристаллов.

Таким образом, определив из эксперимента величину А, можно найти величину 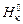. Поскольку Н_k линейно связана с массовой скоростью плавки и силой тока, то, зная 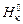, можно оценить соответствующий необходимый режим переплава.

Решение. Определим глубину Н_k для условий эксперимента

Н_k = 0,04(I – 2) = 0,04(18 - 2) = 0,64 м.

Вычислим коэффициент А:

А = [1 + 4(0,64²/0,20²)×0,6²]/0,64² = 38,2 м^–2.

Найдем :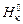

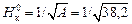= 0,162 м.

Необходимый ток переплава составит

I = 25× 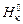+ 2 = 25×0,162 + 2 = 6,05 кА.

107. Допустимая глубина жидкой фазы
в заготовке и максимально допустимая скорость разливки при непрерывной разливке металла

Задача. Определить максимально допустимые значения глубины жидкой фазы и скорости разливки сплава ХН56ВМКЮ на машине полунепрерывного литья заготовок с кристаллизатором круглого сечения.