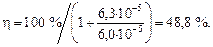11. Рафинирование металла при переплавных процессах
100. Рафинирование металла
от растворенных газов при ВДП
Задача. Определить конечное содержание азота в хромоникелевом сплаве после ВДП, если исходная массовая доля азота равна 0,01 %.
Исходные данные. 1. Линейная скорость наплавления слитка υ0 =
= 3,5×10-5 м/с; линейная скорость оплавления электрода υэл = 5,6×10-5 м/с. 2. Средняя температура зеркала ванны 1830 К; средняя температура торца электрода 1675 К. 3. Торец электрода - плоский. 4. Логарифм коэффициента массопереноса азота в сплаве lgbN (м/с) = -1,106 -
- (5450/T). 5. Логарифм коэффициента активности азота в сплаве lgfN =
= -(5797/T) + 1,072. 6. Равновесным с газовой фазой содержанием азота в поверхностных слоях металла пренебречь. 7. Плотность жидкого сплава r = 7150 кг/м3. 8. Средняя атомная масса сплава МMe = 57,8.
Теория. В общем случае процесс удаления из металла газообразных примесей (азота и водорода) может лимитироваться реакциями как первого, так и второго порядка.
Для переплавного процесса на i-й стадии переплава балансовое уравнение удаления примеси в общем случае имеет вид[1]
G 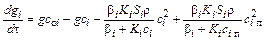 ,
,
где G - масса жидкого металла; c0i - исходное содержание примеси на данной стадии; c i - текущее (конечное) содержание примеси на данной стадии; c i п - содержание примеси на поверхности металла, равновесное с рафинирующей фазой; bi - константа скорости процесса реакции первого порядка; K i - константа скорости процесса реакции второго порядка; g - массовая скорость переплава; r - плотность металла; S i - площадь поверхности металла.
Для установившегося режима переплава dc i /dt = 0, и если пренебречь значением c i п , то балансовое уравнение принимает вид
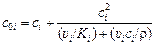 , (11.1)
, (11.1)
где υ i = g/(rS i) - линейная скорость процесса переплава на данной стадии.
Решение уравнения (11.1) относительно с i имеет вид
с i = 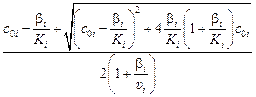 . (11.2)
. (11.2)
Если процесс лимитируется реакцией первого порядка, т.е. bi < K iс i , то
с i » 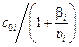 . (11.3)
. (11.3)
Если процесс лимитируется реакцией второго порядка при bi >> K iс i , то
c i » 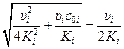 . (11.4)
. (11.4)
Реакцией второго порядка в процессе дегазации металла является реакция [Г] =  {Г2}, химико-десорбционное звено которой может лимитировать процесс. Для этого случая
{Г2}, химико-десорбционное звено которой может лимитировать процесс. Для этого случая
K i = 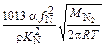 м/(с×%), (11.5)
м/(с×%), (11.5)
где KN - константа в формуле [% N] = (K N /f N) 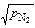 при условии, что pN2 - в атмосферах. Для азота lgKN = -(3607/T) - 0,973 (в никеле); a - коэффициент, характеризующий долю площади поверхности дегазации, незаблокированную ПАВ (кислородом, серой и т.д.), в железе a » 0,018/(0,018 + 2fO [% О] + fS[% S]). В данном расчете можно принять a = 1; r - плотность жидкого металла.
при условии, что pN2 - в атмосферах. Для азота lgKN = -(3607/T) - 0,973 (в никеле); a - коэффициент, характеризующий долю площади поверхности дегазации, незаблокированную ПАВ (кислородом, серой и т.д.), в железе a » 0,018/(0,018 + 2fO [% О] + fS[% S]). В данном расчете можно принять a = 1; r - плотность жидкого металла.
Решение. Оценим величины bi и K i на торце электрода и на поверхности ванны. На торце электрода
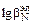 = -1,106 - (5460/1675) = -4,366 =
= -1,106 - (5460/1675) = -4,366 = 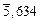 ;
; 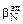 = 4,31×10-5 м/с;
= 4,31×10-5 м/с;
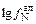 = -(5797/1675) + 1,072 = -2,39 =
= -(5797/1675) + 1,072 = -2,39 = 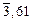 ;
; 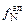 = 4,08×10-3;
= 4,08×10-3;
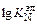 = -(3607/1675) - 0,973 = -3,130 =
= -(3607/1675) - 0,973 = -3,130 = 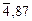 ;
; 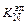 = 7,42×10-4 %/атм1/2;
= 7,42×10-4 %/атм1/2;
Kэл = 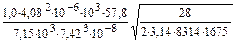 = 1,0×10-2 м/(с×%);
= 1,0×10-2 м/(с×%);
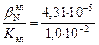 = 4,3×10-3 %;
= 4,3×10-3 %; 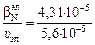 = 0,77.
= 0,77.
На поверхности ванны
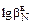 = -1,106 - (5460/1830) = -4,086 =
= -1,106 - (5460/1830) = -4,086 = 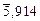 ;
; 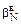 = 8,13×10-5 м/с;
= 8,13×10-5 м/с;
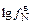 = (-5797/1830) + 1,072 = -2,095 =
= (-5797/1830) + 1,072 = -2,095 = 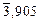 ;
; 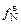 = 8,05×10-3;
= 8,05×10-3;
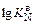 = (-3607/1830) - 0,973 = -2,948 =
= (-3607/1830) - 0,973 = -2,948 = 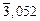 ;
; 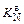 = 1,13×10-3 %/атм1/2;
= 1,13×10-3 %/атм1/2;
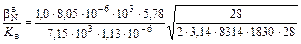 = 1,65×10-2 м/(с×%).
= 1,65×10-2 м/(с×%).
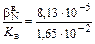 = 4,96×10-3 %;
= 4,96×10-3 %;
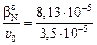 = 2,33.
= 2,33.
Определим долю азота в пленке на торце электрода по формуле (11.2):
[% N]эл = 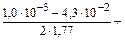
+ 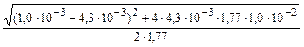 = 6,8×10-3 %.
= 6,8×10-3 %.
В ванне массовая доля азота
[% N]в = 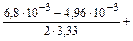
+ 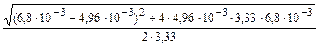 = 4,07×10-3 %.
= 4,07×10-3 %.
Удалилось азота D[% N] = 0,010 - 0,00407 = 0,00593 %. Дегазация составила (D[N]/[N]o)×100 = 60 %.
101. Степень чистоты аргона при плазменной плавке
Задача. Определить необходимую чистоту аргона по азоту при плазменной дуговой плавке чистого железа, если массовая доля азота в железе не должна превышать 1×10-3 %.
Исходные данные. 1. Температуры металла 1873 К, аргонной плазмы – 2200 К. 2. Рабочее давление аргона в печной камере 50 Па. 3. Термодинамические данные:
 {N2} = [N]Fe ; {N2} = [N]Fe ; 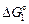 = 10500 + 20,37Т, Дж/моль = 10500 + 20,37Т, Дж/моль
| ||
{N} =  {N2}; {N2}; 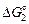 = -471500 + 57,35Т, Дж/моль = -471500 + 57,35Т, Дж/моль
| ||
| {N} = [N]Fe ; DG° = -461000 + 77,72Т, Дж/моль. |
Теория. При вакуумплазменной дуговой плавке поверхность жидкого металла контактирует с плазмой разряда, температура которой выше температуры металла.
В этих условиях, если в плазмообразующем газе содержится азот, он вступает в контакт с металлом, имея степень диссоциации, определяемую температурой плазмы. Поскольку температура плазмы выше температуры металла, то парциальное давление атомарного азота рN у поверхности металла выше равновесного значения рN при температуре металла. Этим объясняется повышенное содержание в металле азота при дуговых видах нагрева металла.
В этих случаях массовая доля растворенного азота, условно равновесного с плазмой, определяется из выражения
[% N] = (KN/fN)pN » (KN/fN) 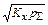 , (11.6)
, (11.6)
где KN - константа реакции {N} = [N] при температуре поверхности металла; K x - константа реакции диссоциации азота {N2} = 2{N} при температуре плазмы; рS - общее парциальное давление азота в газовой фазе.
Если давление выражено в атмосферах, то
lgK x = lg( 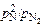 ) = (-49400/T ) + 6,00;
) = (-49400/T ) + 6,00;
lgKN = (24155/T ) - 4,065.
При заданном значении [% N] допустимое общее парциальное давление азота в газовой фазе
рS £ ( 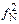 [% N]2)/(
[% N]2)/( 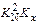 ). (11.7)
). (11.7)
Если азот является примесью в аргоне, то необходимую чистоту аргона по азоту (n, %) можно определить по формуле
n = 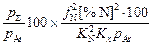 %. (11.8)
%. (11.8)
Решение. При 2200 К
lgK x = (-49400/2200) + 6,00 = -16,455; KN = 3,52×10-17.
При 1873 К lgKN = (24155/1873) - 4,065 = 8,831; KN = 6,80×108.
Для чистого железа fN = 1. Давление аргона составляет рAr = 50×10-5 =
= 5×10-4 атм. Отсюда объемная доля азота в аргоне не должна превышать
n £ (1×10-6×100 %)/(6,82×1016×3,52×1017×5×10-4) = 0,12 %.
102. Исходное содержание летучего компонента в металле при переплаве в вакууме
Задача. Определить необходимое исходное содержание марганца в стали ШХ15 при ЭЛП, при котором после переплава обеспечивается в стали 0,25 % Мn.
Исходные данные. 1. Переплав ведут в кристаллизаторе диаметром 800 мм. 2. Диаметр расходуемой заготовки 600 мм. 3. Массовая скорость переплава 0,15 кг/с. 4. Средний перегрев над температурой ликвидуса на торце заготовки 50 К, на поверхности ванны 200 К. 5. Торец заготовки имеет вид конуса с углом при вершине a = p/4. 6. Температура ликвидуса стали ШХ15 1733 К. 7. Плотность стали ШХ15 при 1873 К 6950 кг/м3, при 1933 К 6800 кг/м3.
Теория. Испарение примесей при переплавных процессах, включая ЭЛП, в основном происходит из пленки жидкого металла на торце заготовки и из ванны. Роль падающих капель сравнительно мала. В отличие от процесса ВДП, где межэлектродное расстояние невелико (~ 20 мм), и следует учитывать конденсацию паров на торце электрода, при ЭЛП расстояние от поверхности ванны до торца заготовки составляет сотни миллиметров. В этом случае процессом конденсации на торце заготовки паров, уходящих с поверхности жидкой ванны, можно пренебречь. При установившемся процессе в единицу времени баланс марганца при испарении из жидкой пленки имеет вид
[% Мn]0 g = [% Мn]пл g + 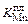 rпл [% Мn]пл Fпл , (11.9)
rпл [% Мn]пл Fпл , (11.9)
где [% Mn]о - исходная массовая доля марганца; [% Мn]пл - массовая доля марганца в пленке; g - массовая скорость плавки; rпл - плотность жидкой стали в пленке; 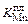 - константа скорости процесса испарения марганца на стадии пленки; Fпл - площадь поверхности пленки металла.
- константа скорости процесса испарения марганца на стадии пленки; Fпл - площадь поверхности пленки металла.
Отсюда
[% Мn]пл = [% Мn]о /[1 + ( 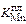 rпл Fпл /g)]. (11.10)
rпл Fпл /g)]. (11.10)
Считая, что в ванну металл попадает с содержанием марганца [% Мn]пл, при испарении из ванны имеем
[% Мn]пл g = [% Мn]кон g + 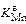 rв[% Mn]кон Fв , (11.11)
rв[% Mn]кон Fв , (11.11)
где [% Мn]кон - конечная массовая доля марганца; KMn - константа скорости процесса испарения марганца на стадии ванны; Fв - площадь поверхности зеркала ванны; rв - плотность жидкой стали в ванне.
Отсюда
[% Мn]кон = [% Mn]пл /[l + ( 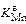 rв Fв /g)]. (11.12)
rв Fв /g)]. (11.12)
Небольшим изменением величины g при переходе от пленки к ванне за счет процесса испарения пренебрегаем. Комбинируя выражения (11.10) и (11.12), получаем
[% Мn]0 = [% Мn]кон[1 + ( 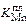 rMnFпл /g)][1 + (
rMnFпл /g)][1 + ( 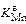 rвFв/g)]. (11.13)
rвFв/g)]. (11.13)
Для марганца в расплавах с железом и никелем процесс испарения при давлении менее 2–3 Па лимитируется внутридиффузионным звеном. По данным Р.А. Алеева и Ю.В. Балкового константа скорости процесса испарения в этом случае имеет вид
KMn = 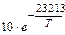 =
= 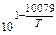 м/с. (11.14)
м/с. (11.14)
Решение. Температура ликвидуса для стали ШХ15 равна 1733 К. Отсюда средняя температура поверхности пленки на торце заготовки составит 1733 + 50 = 1783 К, а на поверхности зеркала жидкой ванны 1733 + 200 = 1933 К.
Соответственно 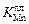 = 101 - (10079/1783) = 10-4,653 = 2,2×10-5 м/с.
= 101 - (10079/1783) = 10-4,653 = 2,2×10-5 м/с.
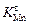 = 101 - (10079/1933) = 10-4,214 = 6,1×10-5 м/с.
= 101 - (10079/1933) = 10-4,214 = 6,1×10-5 м/с.
Оплавляемый торец имеет вид конуса с углом при вершине a = p/4. При диаметре заготовки D = 0,6 м, боковая поверхность конуса равна
Fпл = 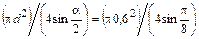 = (p×0,36)/(4×0,3827) =
= (p×0,36)/(4×0,3827) =
= 0,7388 м2.
Площадь зеркала ванны при диаметре D = 0,8 м составит
Fв = (pD2)/4 = (p0,82)/4 = 0,5027 м2.
Отсюда массовая доля марганца в исходном металле составит
[% Мn]0 = 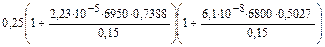 =
=
= 0,25×1,7633×2,39 = 1,05 %.
103. Удаление неметаллических включений
при переплаве в вакууме
Задача. Определить степень удаления непродиссоциировавших оксидов алюминия при ЭЛП в кристаллизаторе диаметром 320 мм.
Исходные данные. 1. Плотность жидкого металла r = 7100 кг/м3. 2. Массовая скорость плавки 0,036 кг/с. 3. Скорость движения частиц глинозема в ванне, определенная по закону Стокса (см. задачу 73), близка к 6×10-5 м/с.
Теория. При переплавных бесшлаковых процессах удаление непродиссоциировавших оксидных включений происходит в основном в результате их всплывания на поверхность жидкой ванны.
Балансовое уравнение удаления включений из металла при установившемся режиме наплавления в единицу времени имеет вид:
[% н.в]0 g = [% н.в]в g s + wFr[% н.в]в , (11.15)
где [% н.в]0 - содержание непродиссоциировавших включений в металле, поступающем в ванну; [% н.в] - то же в металле жидкой ванны; g - массовая скорость плавки; r - плотность жидкого металла; F - площадь поверхности зеркала ванны; w - скорость всплывания частиц глинозема.
Отсюда
[% н.в]в = 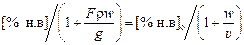 , (11.16)
, (11.16)
где υ = g/Fr - линейная скорость наплавления слитка. Степень удаления включений
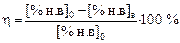 ,
,
или с учетом выражения (11.16)
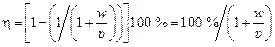 . (11.17)
. (11.17)
Решение. Линейная скорость наплавления слитка
υ = g/Fr = 4g/(pD2r) = 4×0,036/(p×0,322×7100) = 6,3×10-5 м/с.
Степень удаления непродиссоциировавших частиц глинозема вычисляем по формуле (11.17):