Исходные данные. 1. Состав сплава: 10,0 % Сr; 12,0 % Со; 5,3 % Al; 7 % Мо; 7 % W.
2. Al2О3(тв) + SiО2 (тв) = Al2О3 × SiО2(тв) DG° = – 185894 + 1,675Т [8].
3. 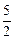 SiO2 (тв) + 2[Al](1 % в Ni) =
SiO2 (тв) + 2[Al](1 % в Ni) =  [Si](1 % в Ni) + Al2O3 ×SiO2(тв). (10.13)
[Si](1 % в Ni) + Al2O3 ×SiO2(тв). (10.13)
На основе расчетов по данным табл. П1 для реакции (10.13)
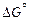 = - 442444 + 68,95Т.
= - 442444 + 68,95Т.
В никеле при 1873 К
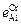 = 0,045;
= 0,045; 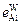 = 0,025;
= 0,025; 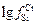 = 1,2 + 0,7 % [% Cr].
= 1,2 + 0,7 % [% Cr].
В никеле 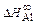 = -153134 Дж/моль.
= -153134 Дж/моль.
Теория. Содержание кремния в жаропрочных сплавах должно быть минимальным, так как образующиеся при охлаждении и кристаллизации этих сплавов силикаты различного состава в виде стекловидных пленок располагаются по границам зерен. Вследствие низкой прочности таких стекол при высокой температуре служебные свойства этих сплавов резко снижаются.
Кремний может попадать в металл из огнеупоров, содержащих кремнезем, в результате восстановления его алюминием и титаном, содержащимися в жаропрочных сплавах, поэтому контакт этих сплавов с кремнесодержащими огнеупорами при плавке и разливке должен быть исключен. Особенно это относится к шамоту, в котором 20–30 % SiO2 не связано в алюмосиликаты. Если в огнеупоре имеется свободный кремнезем, то продуктом реакции является алюмосиликат. Если огнеупор представляет собой чистый алюмосиликат, то продуктом реакции является глинозем.
Решение. Параметр взаимодействия 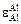 найдем на основании ТКР:
найдем на основании ТКР:
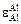 =
= 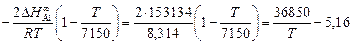 ;
;
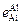 = 4,342×10-3
= 4,342×10-3 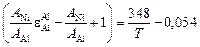 .
.
Для остальных параметров взаимодействия примем:
e Т = (1873/T)e1873;
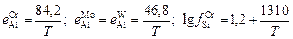 [% Сr].
[% Сr].
Константа реакции (10.13) имеет вид
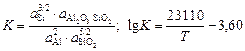 .
.
Считая силлиманит и кремнезем конденсированными фазами, принимаем их активности равными 1. Тогда
lg[% Si] = 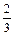 lgK +
lgK + 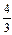 lg fAl - lg fSi +
lg fAl - lg fSi + 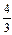 lg[% Al];
lg[% Al];
lg fAl = 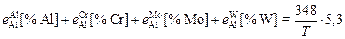 -
-
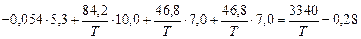 ;
;
lg fSi = 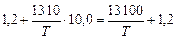 ;
;
lg[% Si] = 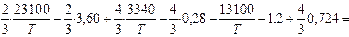 =
= 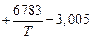 .
.
При T = 1800 К lg[% Si] = (6753/1800) - 3,005 = 0,75; [% Si] = 5,6 %.
При взаимодействии расплава с чистым силлиманитом реакция имеет вид
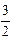 А12O3×SiO2 (т) + 2[Al](1 % в Ni) =
А12O3×SiO2 (т) + 2[Al](1 % в Ni) = 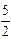 А12O3 (т) +
А12O3 (т) + 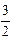 [Si](1 % в Ni).
[Si](1 % в Ni).
По данным о DGo образования силлиманита и данным в табл. П1, П2 имеем
DGo = 22291 + 64,59T.
Считая силлиманит и глинозем конденсированными фазами, имеем
K = 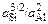 ; lgK = (1164/T ) - 3,374.
; lgK = (1164/T ) - 3,374.
В этом случае
lg [% Si] = 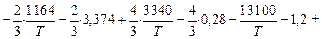
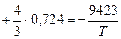 - 2,856.
- 2,856.
При Т = 1800 К lg[% Si] = 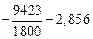 = -8,091,
= -8,091,
[% Si] = 8,11×10-9 %.
Таким образом, при контакте с огнеупорами, содержащими не связанный в алюмосиликаты кремнезем, равновесная массовая доля кремния в сплаве составит 8,9 %. Контакт металла с такими огнеупорами следует исключить. Понижение температуры в данном случае способствует насыщению сплава кремнием.
При контакте с чистым силлиманитом, в котором весь кремнезем связан в силикат, равновесная массовая доля кремния в сплаве равна 8×10-9 %, и контакт с таким огнеупором не загрязняет металл кремнием.
94. Обезуглероживание раскисленного
металла при плавке в вакууме
Задача. Определить, при каких давлениях и температурах термодинамически возможно глубокое обезуглероживание стали типа 03Н18К9М5Т в раскисленном состоянии (в присутствии алюминия).
Исходные данные. Состав стали принять в соответствии с марочным обозначением, концентрации раскислителей – 0,6 % Ti, 0,05–0,15 % Al.
Теория. Высокопрочная мартенситно-стареющая сталь типа 03Н18К9М5Т для повышения качества слитков подвергается дополнительному переплаву в вакуумных дуговых (ВДП) или электронно-лучевых печах (ЭЛП). Одной из наиболее вредных примесей в этом металле является углерод, вызывающий появление охрупчивающих карбидных сеток при [С] > 0,005 %. Выплавить сталь с таким низким содержанием углерода трудно, поэтому актуальной является задача дополнительного обезуглероживания металла при конечном вакуумном переплаве, когда сталь полностью раскислена. Для оценки возможности окисления углерода в присутствии алюминия, необходимо сопоставить равновесные концентрации кислорода, соответствующие этим компонентам. Очевидно, что процесс обезуглероживания возможен только в том случае, когда равновесие с алюминием имеет место при более высоком содержании кислорода, чем равновесие с углеродом (другими словами - чем требуется для обезуглероживания)1.
Термодинамические характеристики реакций взаимодействия кислорода с углеродом и алюминием можно принять по данным табл. П10:
[С] + [О] = СО(г) ; lgK = 1168/T + 2,07; (10.14)
2[Al] + 3[О] = Аl2O3 (т); lgK = 64900/T - 20,63. (10.15)
Известно, что в условиях промышленной вакуумной плавки достигаемые реально концентрации углерода и кислорода соответствуют обычно значениям рCO интервале от 0,1 до 0,01 атм, поэтому расчеты целесообразно вести для этих значений рCO .
Коэффициенты активности fAl , fC и fO при 1873 К можно определить с помощью параметров взаимодействия. Пересчет на другие температуры можно сделать по следующей формуле ТРР:
lg fi (T ) = (1873/T )lg fi (1873 ) . (10.16)
Решение. Рассчитываем равновесные концентрации кислорода для [% С] от 0,005 до 0,02 % и [% Al] от 0,005 до 0,15 % в интервале 1873–2273 К*. Пример расчета для [С] = 0,02 % при 2073 К:
lg fC (1873 ) = -0,075;
lg fC (2073 ) = 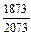 (-0,075) = -0,0676; lg fC (2073 ) = 0,856;
(-0,075) = -0,0676; lg fC (2073 ) = 0,856;
lg fO (2073 ) = 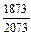 (-0,1625) = -0,147; fO (2073 ) = 0,713.
(-0,1625) = -0,147; fO (2073 ) = 0,713.
Для 2073 К
lgK = 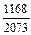 + 2,07 = 2,6334; K =
+ 2,07 = 2,6334; K = 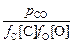 = 430.
= 430.
При рCO = 0,1 атм
[О] = 0,1/(430×0,856×0,02×0,713) = 0,019 %.
Расчеты равновесия алюминия с кислородом затруднены отсутствием необходимых параметров 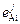 . Для основных легирующих – никеля и кобальта – эти параметры можно оценить с помощью теоретической формулы [3]:
. Для основных легирующих – никеля и кобальта – эти параметры можно оценить с помощью теоретической формулы [3]:
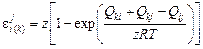 , (10.17)
, (10.17)
где z - координационное число (для сплавов железа можно принять
z = 8); Qki , Qkj , Qij - энергия смешения компонентов. В первом приближении энергии смешения могут быть приняты равными начальным теплотам растворения 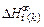 , которые по данным [63, 64] и табл. П2 равны
, которые по данным [63, 64] и табл. П2 равны
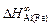 = -62,8;
= -62,8; 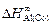 = -91,1;
= -91,1; 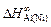 = -153,1;
= -153,1; 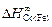 =
=
= 1,42; 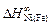 = -10,0 кДж/моль.
= -10,0 кДж/моль.
При 1873 К получим
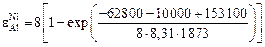 = -6,7;
= -6,7;
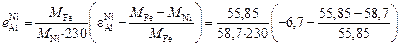 = = –0,0275.
= = –0,0275.
Аналогично 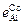 = -0,0086.
= -0,0086.
Таким образом,
lg fAl (1873) = -0,0275×18 - 0,0086×9 = -0,5727; fAl (1873) = 0,268;
lg fAl (2073) = 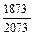 (-0,5727) = -0,5174; fAl (2073) = 0,304;
(-0,5727) = -0,5174; fAl (2073) = 0,304;
lg fAl (2273) = 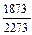 (-0,5727) = -0,4719; fAl (2273) = 0,337.
(-0,5727) = -0,4719; fAl (2273) = 0,337.
Пример расчета для [Аl] = 0,15 % при 2073 К:
lgK = 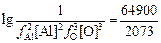 -20,63 = 10,677;
-20,63 = 10,677;
lg[О] = 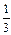 (-lgK - 2lg fAl - 2lg [Al] - 3lg fO) =
(-lgK - 2lg fAl - 2lg [Al] - 3lg fO) = 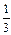 [-10,677 - 2(-0,5177) -
[-10,677 - 2(-0,5177) -
- 2lg0,15 - 3(-0,147)] = -2,5179; [О] = 0,003 %.
Результаты расчетов для остальных температур и концентраций, приведенные в таблице и на рисунке, показывают, что условие обезуглероживания ([О]C < [О]Al) выполняется только при температурах
> 2073 К и рCO < 0,01 атм. Такой перегрев металла (даже на поверхности) при ВДП не наблюдается. При ЭЛП он возможен. Остаточное давление у поверхности металла при ЭЛП также значительно ниже, поэтому в условиях ЭЛП можно ожидать некоторого обезуглероживания металла, несмотря на относительно высокое содержание алюминия. Процесс может идти только на поверхности ванны, без образования пузырей СО. Это определяет малую скорость обезуглероживания, но при низких содержаниях углерода и сравнительно малой скорости переплава она может оказаться достаточной.
Равновесные концентрации кислорода (%) в стали
03Н18К9М5Т при различных условиях
| T, К | pCO = 0,1 атм | pCO = 0,01 атм | 0,05 % (Аl) | 0,15 % (Аl) | ||
| 0,005 % [C] | 0,02 % [C] | 0,005 % [C] | 0,02 % [C] | |||
| [C] + [O] = CO(г) | 2[Al] + 3[O] = Al2O3 (т) | |||||
| 1873 | 0,070 | 0,0175 | 0,0070 | 0,0018 | 0,0006 | 0,0003 |
| 2073 | 0,076 | 0,0190 | 0,0076 | 0,0019 | 0,0063 | 0,0030 |
| 2273 | 0,082 | 0,0204 | 0,0082 | 0,0020 | 0,0473 | 0,0228 |
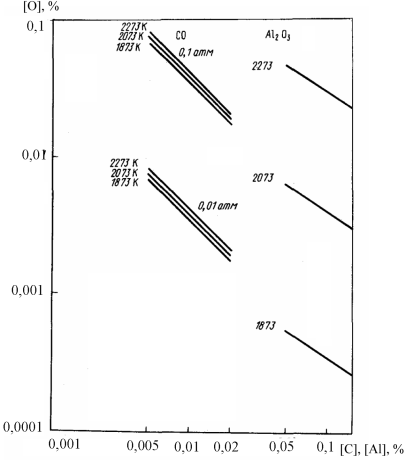
Равновесные концентрации кислорода в расплаве стали типа 03Н18К9М5Т при различных температурах, парциальных давлениях СО и концентрациях углерода и алюминия
Примечания. 1. Как показано В.Г. Дюбановым, Б.С. Ломбергом и др., при ЭЛП стали 03Н18К9М5Т наблюдается удаление углерода и исключается брак по карбидной сетке. При ВДП такого обезуглероживания металла не происходит.
2. Как видно из рисунка, повышение температуры сдвигает равновесие реакции раскисления металла алюминием (10.15) значительно сильнее, чем реакции раскисления углеродом. Это согласуется с табличными данными о величинах стандартных энтальпий образования Аl2O3 и СО (кДж/ (г×ат) О2): -1681/3 = -560 и -118 соответственно (см. табл. П1). Очевидно, что качественно влияние температуры можно было предсказать и без вычислений. Для более точного предсказания лучше пользоваться не стандартными энтальпиями образования оксидов, а теплотами реакций (10.14) и (10.15), которые можно определить по соответствующим уравнениям для lgK:
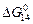 = -2,303RT lgK = -19,14Т
= -2,303RT lgK = -19,14Т 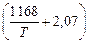 = -22360 - 39,6Т Дж;
= -22360 - 39,6Т Дж;
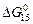 = -19,14T
= -19,14T 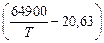 = -1242000 + 394,9T Дж.
= -1242000 + 394,9T Дж.
Видно, что энтальпия реакции (10.15) (-1242/3 = -414 кДж/(г×ат) О2) значительно больше по абсолютной величине, чем 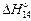 (-22,36 кДж).
(-22,36 кДж).
95. Влияние футеровки на раскисление металла углеродом при плавке в вакууме
Задача. Рассчитать изменение концентраций углерода и кислорода и произведение [С][О] = m при вакуумной плавке металла без учета взаимодействия его с футеровкой (при бестигельной плавке или при плавке в большегрузной печи, когда удельная поверхность контакта металла с тиглем относительно мала). Оценить влияние футеровки на конечные концентрации углерода и кислорода.
Исходные данные и рекомендуемые допущения. Температура
Т = 1873 К. Давление в печи: р = 0,0067 Па (6,6 × 10–8 атм). Натеканием воздуха в печь пренебречь. Исходное содержание углерода: [С]0 = 0,04 %. Исходное содержание кислорода [О]0 принять на уровне равновесного с [С]0 при pCO = 101325 Па (1 атм). В термодинамических расчетах принять pCO = р, 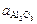 = 1, fC = fO = fAl = 1.
= 1, fC = fO = fAl = 1.
Теория. Взаимодействие растворенных в металле углерода и кислорода описывается реакцией:
[С] + [O] = СО(г); (10.18)
K = pCO/[C][О]; lgK = (1168/T ) + 2,07; (10.19)
Согласно уравнению (10.19) связь между равновесными [C] и [О] при заданных давлениях pCO (6,6 × 10–8 и 1 атм) выражается на графике зависимости lg[% О] от lg [% С] (см. рисунок) прямыми 1–2 и 1¢–2¢.
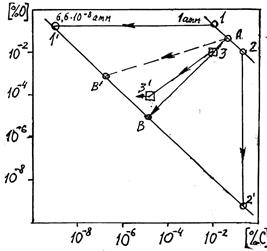
Изменение концентраций углерода и кислорода в железе при вакуумной плавке без учета и с учетом взаимодействия металла с футеровкой (линии АВ и A В¢, соответственно). Линия 3–3¢ – экспериментальные данные; стрелка у точки 3¢ означает, что действительное содержание углерода несколько ниже показанного на графике (анализ выполняли на пределе чувствительности метода)
При понижении давления в печи протекание реакции (10.18) должно сопровождаться изменением состава металла от исходного состояния на прямой 1–2 до какой-то из точек на прямой 1¢–2¢. Положение этой конечной равновесной точки зависит от содержания кислорода (от поступления кислорода в металл, например, из тигля, или расходования его на другие процессы). Если металл не получает и не расходует кислород (при плавке без взаимодействия с футеровкой), то его состав изменяется в ходе реакции (10.18) согласно стехиометрическому соотношению:
[С]0 – [С] = ([О]0 – [О])×12/16. (10.20)
Решение. Вычислим исходную концентрацию кислорода [О]0, равновесную с [С]0 = 0,04 % при pCO = 1 атм. По формуле (10.19) определим K1873:
lgK = (1168/1873) + 2,07 = 2,69; K = 495;
[C][O] = m(1 атм) = 1/495 = 0,002.
Отсюда
0,04[О]0 = 0,002; [О]0 = 0,05 %.
На графике исходный состав металла характеризуется, таким образом, точкой А.
Уравнение стехиометрической линии согласно (10.20) имеет вид:
[O]стех = [O]0 – ([С]0 – [С]) × 16/12. (10.21)
Эту линию можно построить, задавая различные значения [С] < [С]0 и вычисляя соответствующие им значения [O]стех. Результаты расчетов приведены ниже:
| [C] | 0,03 | 0,003 | 0,001 | 0,0001 | 0,00001 |
| [O]стех | 0,0367 | 0,00400 | 0,00133 | 0,000133 | 0,0000133 |
| [O]равн | 0,00000000443 | 0,0000000443 | 0,000000133 | 0,00000133 | 0,0000133 |
Стехиометрическая линия на графике (см. рисунок) – это линия АВ. Точка В находится на пересечении стехиометрической кривой с равновесной прямой 1¢ – 2¢.
Форма кривой АВ в данном случае соответствует примерно эквивалентным содержаниям углерода и кислорода (без избытка или недостатка того или другого) в интервале между точками А и В. При других начальных составах, характеризуемых точками 1 и 2, стехиометрические линии могут почти совпадать с вертикалью (2–2¢) или горизонталью (1–1¢), в заисимости от того, который из элементов находится в избытке.
При взаимодействии металла с футеровкой – с тиглем из Al2O3, например, по реакции
Al2O3 (т) = 2[Аl] + 3[O] (10.22)
содержание кислорода в металле будет увеличиваться. Равновесие с углеродом, соответствующее линии 1¢–2¢, установится в этом случае при более высоком содержании кислорода. Примером такого взаимодействия является линия АВ¢. Экспериментальные данные, полученные в работе [65], выражаются линией 3–3¢.
Примечания. 1. При взаимодействии металла с футеровкой путь характеристической точки на графике из начального в конечное положение, из А в В¢, определяется соотношением скоростей реакций (10.18) и (10.22). Если реакция (10.18) имеет относительно большую скорость, то путь точки приближается к линии ABВ¢. Если скорости соизмеримы, то ближе к реальности прямая AВ¢.
2. При явном избытке одного из компонентов ([С] или [О]) его содержание практически не изменяется вследствие недостатка второго реагента, например, при рCO = 1 атм и [С]0 = 0,01 % [О]0 = 0,2. В этом случае кислород – в избытке, поэтому его содержание при окислении 0,01 % углерода практически не изменяется (линия на рисунке становится горизонтальной).
3. Принятое в расчете допущение о равенстве рCO остаточному давлению реализуется только в специальных (например, в лабораторных) условиях, когда сравнительно малая скорость беспузырькового выделения СО (через открытую поверхность металла) оказывается достаточной для достижения равновесия. В обычных условиях действует условие пузырькового выделения СО: рCO > р + rgh + (2s/r) (см. задачу 85).
4. На рисунке для сопоставления с расчетными результатами представлены экспериментальные данные – линия 3–3¢ [65]. Данные получены в лабораторных условиях, близких к расчетным, при использовании специальных методов анализа металла. Содержание алюминия в металле до и после опыта было менее предела обнаружения (10–4 %). В других опытах тех же авторов при плавке образцов, содержащих 0,2 % С, концентрация алюминия увеличилась за 1 ч с 0,019 до 0,033 %. Как видно из графика, расчетные данные довольно близки к экспериментальным.
5. При увеличении массы металла в тигле влияние футеровки уменьшается, поскольку удельная поверхность контакта металла с тиглем снижается. Особенно мало влияние реакций с участием трех фаз (например, реакции (10.18) и др.), так как они идут на тонкой линии, где контактируют три фазы. В крупных промышленных вакуумных печах переход кислорода в металл из футеровки очень мал. В лабораторных условиях и в малых промышленных агрегатах его необходимо учитывать.
96. Минимальная концентрация газов
в стали при вакуумной плавке
Задача. Определить минимальные концентрации кислорода, азота и водорода в жидкой низкоуглеродистой стали при вакуумплавке.
Исходные данные. 1. Т = 1873 К. 2. Поверхностное натяжение стали, содержащей углерод и кислород, s = 1500 мДж/м2. 3. KH = 0,0027;
KN = 0,044; K = рCO /([С][О]) = 490.
Теория. Рассмотрим наиболее простой случай, когда пузырь газа находится в поверхностном слое hм = r, рост ® 0, hш ® 0 (см. рисунок) (см. задачу 85). Тогда давление газа в пузыре равно
рг = pм gr + 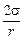 . (10.23)
. (10.23)
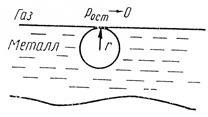
Схема расположения пузыря газа
Продифференцируем уравнение (10.23) по r и приравняем его нулю. Это позволит вычислить минимальный радиус (rmin), при котором пузырь может существовать
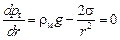 ; rmin =
; rmin = 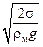 . (10.24)
. (10.24)
В этом случае минимальное давление в пузыре можно определить, если подставить значение rmin в уравнение (10.23):
pmin = 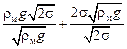 ; pmin =
; pmin = 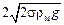 . (10.25)
. (10.25)
Решение. По формуле (10.25) вычисляем pmin:
pmin = 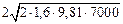 = 937,5 Н/м2
= 937,5 Н/м2
или
pmin = 0,00956 атм, pmin » 0,01 атм.
Если давление в пузыре < 0,01 атм, то даже в самом благоприятном случае (pост ® 0, hм = r, hш = 0) пузырь не будет существовать. Перейдем от давления к концентрациям. При 1873 К для водорода [H] = = KH 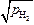 = 0,0027
= 0,0027 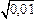 = 0,00027 %; для азота [N] =
= 0,00027 %; для азота [N] = 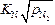 =
=
= 0,044 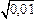 = 0,0044 %; для кислорода [О] = pCO/(K×[С]) = 0,01/(490×0,1) = = 0,0004 % при [С] = 0,1 %.
= 0,0044 %; для кислорода [О] = pCO/(K×[С]) = 0,01/(490×0,1) = = 0,0004 % при [С] = 0,1 %.
Примечание. В расчете предполагается, что кинетические затруднения (образование зародышей пузырей и др.) устранены и роли не играют.
97. Лимитирующая стадия испарения
Задача. Определить лимитирующую стадию испарения марганца из сплава с железом при вакуумной индукционной плавке.
Исходные данные. 1. После 10-мин выдержки при 1873 К концентрация марганца в расплаве железа снизилась с 4,29 до 0,31 %. 2. Объем расплава V = 14,93×10-6 м3, площадь поверхности металл–газ S = 5,56×10-4 м2. 3. rспл = 6900 кг/м3. 4. gMn = 1,43. 5. 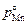 = 5400 Па. 6. рост < 0,133 Па.
= 5400 Па. 6. рост < 0,133 Па.
Теория. Процесс испарения включает три последовательные стадии: 1) внутридиффузионную - перенос компонента из объема расплава к поверхности раздела металл–газ; 2) испарение с открытой поверхности; 3) внешнюю (массоперенос в газовой фазе). При достаточно низких остаточных давлениях (рост < 0,133 Па) третья стадия, как правило, процесса испарения в целом не лимитирует. Рассмотрим последовательно первую и вторую стадию.
1. Поток (W1) компонента в жидком расплаве описывается уравнением
W1 = K1(c - cп), (10.26)
где K1 - коэффициент массопередачи примеси в расплаве; с и cп концентрации примеси в объеме и в приповерхностном слое.
2. Константа скорости испарения (K2) марганца с открытой поверхности при рост < 0,133 Па описывается следующим уравнением основанным на формуле Лангмюра:
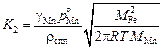 . (10.27)
. (10.27)
Здесь MFe и MMn - атомные массы железа и марганца.
Скорость испарения в лангмюровском режиме
W2 = K2cп. (10.28)
В стационарных условиях
W1 = W2 = W; K1(с - сп) = K2сп . (10.29)
Отсюда
cп = [K1 /(K2 + K1)]c . (10.30)
Подставив значение cп в уравнение (10.28), с учетом выражения (10.29) получим
W = [(K1K2)/(K1 + K2)]с . (10.31)
Обозначив (K1K2)/(K1 + K2) = Kэф, получим
W = Kэф с. (10.32)
Тогда
W = -dc/dt = Kэф(S/V )c . (10.33)
Интегрируя уравнение (10.33), получаем
ln(со/с) = Kэф(S/V )t . (10.34)
По уравнению (10.34) можно определить Kэф . Из уравнений (10.28) и (10.32) следует
K2 cп = Kэф с или cп /с = Kэф /K2. (10.35)
Если (cп /с) ® 0, то процесс испарения протекает во внутридиффузионной области (процесс лимитируется массопередачей в расплаве). Если (cп /с) ® 1, то реализуется кинетический режим испарения.
Решение. Вычислим K2 по формуле (10.27):
K2 = 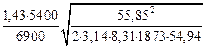 = 2,7×10-2 м/с.
= 2,7×10-2 м/с.
Теперь вычислим Kэф по уравнению (10.34):
Kэф = 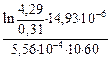 = 1,2×10-4 м/с.
= 1,2×10-4 м/с.
Тогда по уравнению (10.35) сп/с = (1,2×10-4)/(2,7×10-2) = 4,3×10-3.
Таким образом, испарение марганца протекает в диффузионном режиме.
98. Кинетические характеристики
процесса испарения примеси
Задача. Определить лимитирующее звено процесса испарения меди из железа.
Исходные данные. 1. Основа сплава - железо, испаряющаяся примесь - медь. 2. При 1873 К константа скорости испарения меди при р = 100 Па равна 2,21×10-5 м/с, а при р = 0,133 Па - 9,0×10-5 м/с. 3. Коэффициент активности меди в железе gCu = 10. 4. Плотность жидкого железа r = 7×103 кг/м3. 5. Давление насыщенности пара чистой меди при 1873 К равно 106 Па.
Теория. Процесс испарения примеси из металла может в общем случае лимитироваться одним из трех последовательных звеньев этого процесса - массопереносом в металле, десорбцией с поверхности и массопереносом в газовой фазе. При стационарном процессе испарения потоки вещества, диффундирующего через непромешиваемый слой жидкого металла, испаряющегося с поверхности и диффундирующего через непромешиваемый слой газовой фазы, одинаковы.
Поток вещества примеси с единицы площади поверхности испарения является в данном случае скоростью испарения w, кг/(м2×с).
Если средняя концентрация примеси в объеме металла равна с, то для стационарного режима можно записать
w = Kэф с, (10.36)
где Kэф - эффективная константа процесса испарения.
Если обозначить константу скорости процесса внутреннего массо-переноса K1 , константу скорости акта испарения K2 и константу скорости массопереноса в газе через K3 , то
1/Kэф = (1/K1) + (1/K2) + (1/K3). (10.37)
Размерность Kэф зависит от выбора размерности с. Если с выражается как массовая концентрация в процентах, то размерность [Kэф] = = кг/(м2×с×100 %). Однако чаще всего на практике выбирают размерность [Kэф] = м/с. В этом случае размерность с должна составлять [с] = кг/м3, т.е. выражаться единицами концентрации. Переход от массовой доли [% с] к концентрации с в этом случае производят по формуле
c = [% c](r /100), (10.38)
где r - плотность жидкого металла - основы сплава.
В данной задаче принят второй вариант выбора размерности Kэф.
Константы K1 и K2 часто объединяются в одну константу K0 = = (K1K2)/(K1 + K2), не зависящую от давления газовой фазы (р). В отличие от K0 величина K3 существенно зависит от р. Зависимость эта определяется критериальным уравнением массопередачи
Sh = C(Gr×Sc)i, (10.39)
где Sh - критерий Шервуда; Gr - критерий Грасгофа; Sc - критерий Шмидта; С и i - постоянные коэффициенты. Для Gr×Sc = 103–109, С = = 0,54, i = 0,25.
При i = 0,25 зависимость K3 от р имеет вид
K3 = 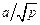 , (10.40)
, (10.40)
где а - коэффициент, зависящий от рода газа, температуры и диаметра зеркала ванны металла.
Эффективная константа Kэф в этом случае также зависит от давления:
Kэф = K0/(1 + (K0 /a) 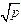 ). (10.41)
). (10.41)
При (K0 /a) 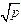 << 1 давление газовой фазы практически не влияет на величину Kэф. Заметную роль изменение давления начинает играть при (K0 /a)
<< 1 давление газовой фазы практически не влияет на величину Kэф. Заметную роль изменение давления начинает играть при (K0 /a) 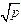 > 0,2, а при (Kэф /a)
> 0,2, а при (Kэф /a) 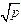 > 0,5 процесс начинает лимитироваться массопереносом в газовой фазе.
> 0,5 процесс начинает лимитироваться массопереносом в газовой фазе.
При каждом данном значении р в выражении для Kэф имеются две неизвестные величины: K0 и а. Таким образом, при наличии данных о значениях Kэф как минимум при двух различных значениях р можно оценить величины K0 и а. В свою очередь знание величины K0 позволяет оценить величины K1 и K2 .
По уравнению Лангмюра для стадии акта испарения примеси
w = 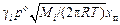 = K2cп , (10.42)
= K2cп , (10.42)
где gi - коэффициент активности примеси; po - давление насыщенного пара примеси; М i - атомная масса примеси; R - универсальная газовая постоянная; R = 8314 Дж/(К×кг-моль); xп - мольная доля примеси в поверхностном слое; cп - концентрация примеси в поверхностном слое.
Из формулы (10.42) следует, что
K2 = 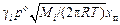 = (xп/cп). (10.43)
= (xп/cп). (10.43)
При близких атомных массах основы сплава и примеси и малых содержаниях примеси приближенно можно считать, что
xп/cп » Мм /(М i r), (10.44)
где Mм - атомная масса основы сплава. Тогда
K2 » 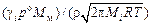 . (10.45)
. (10.45)
При известных значениях K0 и K2 имеем
K1 = (K0K2)/(K2 - K0). (10.46)
В глубоком вакууме при K1 /K2 < 1,0, процесс лимитируется внутренним массопереносом, а при K1 /K2 > 1,0 - актом испарения. При необходимости сравнить все три звена, сравнивают величины K1 , K2 и K3 . Лимитирующим является звено с наименьшим K i .
Решение. На основании исходных данных составим и решим систему уравнений, связывающих величины Kэф и р:
2,21×10-5 = K0 /[1 + (K/a) 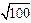 ];
];
9,0×10-5 = K0 /[1 + (K/a) 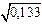 ].
].
В результате решения системы получим K0 = 1,02×10-4 м/с, а = = 2,82×10-4 м×Па1/2/с. Найдем K2 по формуле (10.45), считая для меди MCu = 63,5 кг-моль,
K2 = (10×106×55,8)/(7000 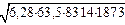 ) = 1,08×10-4 м/с
) = 1,08×10-4 м/с
и величину K1 по формуле (10.46):
K1 = (1,02×10-4×1,08×10-4)/(1,08×10-4 - 1,02×10-4) = 1,84×10-3 м/с.
Определим K3 при р = 100 Па и р = 0,133 Па.
При р = 100 Па K3 = 2,82×10-4/ 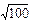 = 2,82×10-5 м/с.
= 2,82×10-5 м/с.
При р = 0,133 Па K3 = 2,82×10-4/ 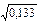 =7,75×10-4 м/с.
=7,75×10-4 м/с.
Таким образом, полученные результаты показывают, что в условиях экспериментов при р = 100 Па процесс лимитируется массопереносом в газовой фазе, а при р = 0,133 Па и ниже лимитирующим звеном является акт испарения.
99. Коэффициент испарения компонента
в условиях вакуумной плавки
Задача. Определить коэффициент испарения (a) марганца из расплава Fe–4 % Mn при плавке в ВИП.
Исходные данные. 1. Вместимость ВИП – 1000 кг, диаметр тигля 0,51 м, продолжительность вакуумирования 600 с, плотность сплава r = 7000 кг/м3. 2. Т = 1873 К. 3. Давление пара железа 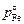 = 6,9 Па.
= 6,9 Па.
4. ln gFe = 0,389 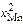 . 5. Константа скорости испарения марганца
. 5. Константа скорости испарения марганца
KMn = 1,16×10-4 м×с-1. 6. 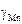 = 1,43 при 1873 К.
= 1,43 при 1873 К.
Теория. Полнота процесса испарения при вакуумной плавке характеризуется коэффициентом испарения Олетте (a)
a = (gi 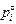 )/(gFe
)/(gFe 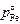 )
) 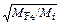 , (10.47)
, (10.47)
где gi , gFe , 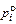 ,
, 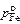 , M i , MFe - коэффициенты активностей, давления паров и молекулярные массы примесного элемента и железа. Зная a, можно оценить относительные потери элементов в процессе плавки в вакууме
, M i , MFe - коэффициенты активностей, давления паров и молекулярные массы примесного элемента и железа. Зная a, можно оценить относительные потери элементов в процессе плавки в вакууме
u i = 100 - 100[1 - (uFe /100)]a, (10.48)
где u i и uFe - относительные потери i-й примеси и железа.
Коэффициент a можно вычислить по уравнению (10.47) или определить экспериментально. В первом случае необходимо знать табличные данные по коэффициентам активностей и давлениям паров компонентов, во втором - опытные данные по скорости испарения элементов, которая описывается уравнением
-dc/dt = K(S/V)c, (10.49)
где S и V - поверхность и объем расплава.
Проинтегрировав выражение (10.49) в пределах t = 0 и t; с = со и с, получим
ln(со /с) = K(S/V )t. (10.50)
Если процесс испарения описывается уравнением первого порядка, то экспериментальные результаты, отложенные на графике в координатах ln(со /с)–t аппроксимируются прямой линией, угловой коэффициент которой характеризует константу скорости испарения. Для чисто кинетического режима константа скорости испарения примеси может быть вычислена по следующему уравнению, основанному на уравнении Лангмюра:
K i = 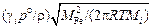 , (10.51)
, (10.51)
где r - плотность сплава; R, Т - универсальная газовая постоянная и температура.
Решение. По уравнению (10.50) определим конечное содержание марганца
ln(4,0/cMn) = (1,16×10-4×600×3,14×0,2552×7000)/1000; cMn = 3,62 %.
Относительные потери марганца составят 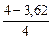 ×100 = 9,5 %.
×100 = 9,5 %.
Константу скорости испарения железа определим по формуле (10.51):
KFe = [(1×6,9)/(7×103)] 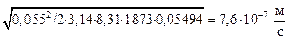 .
.
Теперь по формуле (10.50) вычислим конечную концентрацию железа:
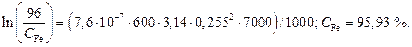
Относительные потери железа [(96 – 95,93)/96]×100 = 0,07 %.
Для определения a прологарифмируем уравнение (10.48) и подставим соответствующие значения uMn и uFe:
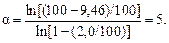
Поскольку a > 1, то в процессе испарения в расплаве снижается содержание марганца. Если a < 1, то расплав будет обогащаться растворенным компонентом.
Примечание. Расчетное значение a, вычисленное по уравнению (10.47), равно
aрасч = [(1,43×5400)/(1×6,9)] 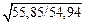 = 1128.
= 1128.
Существенное различие между aрасч = 1128 и a = 5 связано с тем, что уравнение (10.47) выведено для случая свободного испарения. Вместе с тем известно, что марганец испаряется в кинетико-диффузионном режиме. Таким образом, теоретические коэффициенты испарения совпадают с экспериментальными только в том случае, когда процесс протекает в кинетическом режиме.








