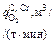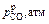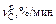Результаты расчета изменения состава и температуры металла по ходу аргоно-кислородной продувки
| t, мин | Состав металла, % | T, К | nFe, %/мин | nSi, %/мин |
|
|
| nС, %/мин | nСr, %/мин | n T, К/мин | ||
| C | Cr | Si | ||||||||||
| Период I | ||||||||||||
| 0 | 1,160 | 17,29 | 0,400 | 1748,00 | 0,039 | 0,044 | 0,088 | 1,190 | – | 0,0095 | 0 | 11,84 |
| 1 | 1,150 | 17,29 | 0,356 | 1759,84 | 0,039 | 0,044 | 0,088 | 1,300 | – | 0,0095 | 0 | 11,82 |
| 2 | 1,141 | 17,29 | 0,312 | 1771,66 | 0,039 | 0,044 | 0,088 | 1,410 | – | 0,0095 | 0 | 11,80 |
| 7 | 1,085 | 17,29 | 0,090 | 1830,77 | 0,039 | 0,044 | 0,088 | 2,0 | – | 0,095 | 0 | 11,72 |
| 8 | 10,75 | 17,29 | 0,046 | 1842,49 | 0,039 | 0 | 0,442 | 2,210 | – | 0,0474 | 0 | 3,34 |
| 22 | 0,420 | 17,29 | 0,046 | 1889,06 | 0,039 | 0 | 0,442 | 1,020 | – | 0,0474 | 0 | 3,28 |
| 23 | 0,373 | 17,29 | 0,046 | 1892,34 | 0,038 | 0 | 0,425 | 0,910 | 0,1380 | 0,0456 | 0 | 2,91 |
| Период II | ||||||||||||
| 24 | 0,327 | 17,29 | 0,046 | 1895,25 | 0,038 | 0 | 0,425 | 0,807 | 0,0560 | 0,0456 | 0 | 2,91 |
| 25 | 0,282 | 17,29 | 0,046 | 1898,16 | 0,038 | 0 | 0,425 | 0,700 | 0,0313 | 0,0313 | 0,046 | 6,38 |
| 26 | 0,251 | 17,24 | 0,046 | 1904,54 | 0,038 | 0 | 0,425 | 0,651 | 0,0250 | 0,0250 | 0,068 | 7,40 |
| 32 | 0,132 | 16,73 | 0,046 | 1959,25 | 0,038 | 0 | 0,425 | 0,525 | 0,0148 | 0,0148 | 0,1016 | 10,36 |
| 33 | 0,118 | 16,63 | 0,046 | 1969,61 | 0,020 | 0 | 0,221 | 0,507 | 0,0280 | 0,0237 | 0 | –0,57 |
| Период III | ||||||||||||
| 34 | 0,094 | 16,63 | 0,046 | 1969,04 | 0,020 | 0 | 0,221 | 0,400 | 0,00182 | 0,0182 | 0,018 | 0,07 |
| 35 | 0,076 | 16,61 | 0,046 | 1969,70 | 0,020 | 0 | 0,221 | 0,323 | 0,0130 | 0,0130 | 0,035 | 1,93 |
| 39 | 0,0375 | 16,42 | 0,046 | 1980,84 | 0,020 | 0 | 0,221 | 0,174 | 0,0057 | 0,0057 | 0,060 | 3,72 |
| 39,5 | 0,0346 | 16,39 | 0,046 | 1982,70 | ||||||||
| Примечание. В таблицу внесены округленные значения; промежуточные значения в каждом из периодов не приводятся. | ||||||||||||
Как видно из приведенного ниже сопоставления, расчетные значения (знаменатель) [С], [Сr] и T в конце каждого периода достаточно близки к экспериментальным (числитель):
| Н.п. | С, % | Cr, % | Т, К | |
| 1,16 | 17,29 | 1748 | ||
| I | 0,41/0,37 | 16,9/17,29 | 1923/1892 | |
| II | 0,12/,0,118 | 16,7/16,3 | 1998/1969 | |
| III | 0,047/0,0346 | 16,45/16,39 | 2003/1982 | |
| Примечание. Н.п. - начало продувки, I–III - моменты окончания периодов продувки. | ||||
Примечание. Образование оксида с формулой Cr3O4 экспериментально не зарегистрировано. Формула принята только потому, что она обеспечила наилучшее согласование между собой равновесных опытных значений [Cr], [C], и Т при рСО = 1 атм. Значение DGº образования Cr3O4 получено обратным расчетом из 9.2.
83. Распределение серы
между металлом и шлаком
Задача. Определить количество шлака, необходимое для десульфурации 1 т стали в ковше при 1923 К.
Исходные данные.
1. Состав шлака: 50 % СаО; 50 % Al2O3. 2. Содержание алюминия и серы в конечном металле: 0,010 % [Аl], 0,005 % [S]. 3. Содержание серы в исходном металле 0,015 %.
Теория. В условиях сталеварения обычно валентность серы nS = -2 (см. задачу 24), поэтому растворимость серы в шлаке определяется соотношением
(S) = 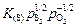 ,
,
где S - концентрация серы в шлаке.
Константу K(S) называют сульфидной емкостью шлака, и если массовое содержание серы выражено в процентах, то ее обозначают символом cS (см. задачу 29):
(% S) = 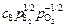 . (9.27)
. (9.27)
Окислительный потенциал системы ( pO2) и давление паров серы ( pS2), необходимые для расчета равновесного содержания серы в шлаке (% S), могут быть найдены по заданным значениям [Аl] и [S] из реакций
2[Аl] + 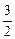 О2 = (Аl2О3);
О2 = (Аl2О3);
[S] =  S2 .
S2 .
Сульфидная емкость cS шлака заданного состава оценивается при помощи одного из теоретических методов или принимается на основании опубликованных экспериментальных данных.
Решение. На основании справочных данных принимаем значения DG реакций:
 О2(г) = [% О]Fe ; DGº = -117200 - 7,89Т, Дж;
О2(г) = [% О]Fe ; DGº = -117200 - 7,89Т, Дж;
lg K[O] = 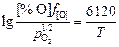 + 0,151;
+ 0,151;
K[O] (1923 К) = 2154; (9.28)
 S2 (г) = [% S]Fe ; DGº = -7200 – 10,26Т, Дж;
S2 (г) = [% S]Fe ; DGº = -7200 – 10,26Т, Дж;
lgK[S] = 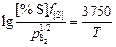 + 0,535;
+ 0,535;
K[S] (1923 К) = 309; (9.29)
2[Al] + 3[O] = Al2O3 (т) ; DGº = -1199700 – 372,2Т, Дж;
lgK4 = 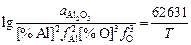 - 19,431;
- 19,431;
K4 (1924 К) = 1,36×1013. (9.30)
Чтобы не усложнять примера, коэффициенты активности fC , fO , fAl и gAl2O3 принимаем равными 1. Решая совместно уравнения
(9.27) – (9.30), определяем содержание серы в шлаке после обработки металла:
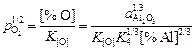 ,
,
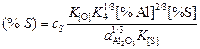
Пользуясь данными [4, с. 118], получим
lg cS = -2,37, cS = 4,3×10-3.
Вычисляем содержание серы в конечном шлаке:
(% S) = 43×10-3 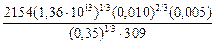 = 0,24.
= 0,24.
Из 1 т металла должно перейти в шлак [(0,015 - 0,005)×1000 кг]/100 =
= 0,1 кг серы. Для этого потребуется шлака (0,1×100)/(% S) =
= (0,1×100)/0,24 = 41,7 кг.
Примечание. Найденное количество шлака является теоретически необходимым. Поскольку в реальных условиях равновесие как правило не достигается, то количество шлака приходится увеличивать.
84. Дегазация стали продувкой
жидкого металла в ковше аргоном
Задача. Определить количество аргона, необходимого для продувки жидкой стали ШХ15 в ковше при 1873 К через фурму или пористые элементы футеровки для снижения концентрации водорода.
Исходные данные. 1. Масса металла в ковше g = 40 т. 2. Исходная и конечная концентрации водорода равны [H]исх = 6×10-4 %,
[Н]кон = 3×10-4 %. 3. Константа (KH) равновесия реакции Н2 = 2[Н] при 1873 К равна 0,73×10-5.
Теория. В соответствии с формулой Геллера [56] уравнение, описывающее зависимость концентрации водорода от количества продуваемого аргона VAr (м3), имеет вид
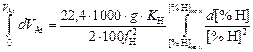 . (9.31)
. (9.31)
После интегрирования (при 1873 К) получим
VAr = 0,82 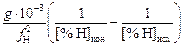 . (9.32)
. (9.32)
Решение. Коэффициент активности водорода в жидкой стали ШХ15 (1 % С, 1,5 % Сr) вычисляем по параметрам взаимодействия (см. задачу 62): fH = 1,07. Тогда VAr = [(0,82×10-3×40)/(1,072)][( 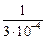 ) -
) -
– ( 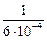 )] = 47 м3.
)] = 47 м3.
Примечания. 1. Расчет сделан с учетом того, что Н2 в пузыре аргона находится в равновесии с водородом, растворенным в жидкой стали. В связи с этим размер пузырей аргона, так же как и продолжительность продувки, роли не играют. Для водорода обычно наблюдают удовлетворительное соответствие между опытными и расчетными данными, что указывает на достижение равновесия ( 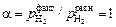 ) и отсутствие диффузионных сопротивлений в объеме металла. Для азота в большинстве случаев равновесие не достигается (a = 0,2–0,4). Это связано с тем, что при продувке азотом процесс лимитируется массопереносом азота из объема расплава к поверхности пузыря аргона. Другими словами, равновесие между азотом в пузыре аргона с азотом, растворенным во всем объеме металла, не достигается, хотя между поверхностным слоем и пузырем равновесие может иметь место.
) и отсутствие диффузионных сопротивлений в объеме металла. Для азота в большинстве случаев равновесие не достигается (a = 0,2–0,4). Это связано с тем, что при продувке азотом процесс лимитируется массопереносом азота из объема расплава к поверхности пузыря аргона. Другими словами, равновесие между азотом в пузыре аргона с азотом, растворенным во всем объеме металла, не достигается, хотя между поверхностным слоем и пузырем равновесие может иметь место.
2. Чтобы ввести в металл требуемое количество аргона (47 м3) за реальное время продувки (10 мин), необходим расход аргона 4,7 м3/мин. Это соответствует интенсивности продувки
0,12 м3/(т×мин). Такие интенсивности при продувке в ковше недостижимы из-за слишком бурного кипения металла. Поэтому удаление в ковше водорода из металла без вакуума практически невозможно. Процесс можно реализовать только в аргоно-кислородном конвертере при продувке с интенсивностью 1 м3/(т×мин).
85. Условие пузырькового
выделения газов из стали
Задача, Вычислить концентрацию водорода в стали 30ХГСА, при которой в ходе вакуумирования возможен пузырьковый механизм выделения водорода с заданной глубины металлической ванны.
Исходные данные. 1. Состав стали: 0,3 % С; 1 % Сr; 1 % Мn; 1 % Si. 2. Плотность расплава r = 7,0×103 кг/м3. 3. Поверхностное натяжение металла s = 1,68 Дж/м2. 4. Начальный радиус пузыря r = 5×10-4 м. 5. Температура 1873 К. 6. Остаточное давление в вакуумной камере рост = 4×102 Па. 7. Глубина ванны h = 0,5 м.
Теория. Процесс растворения водорода в стали (или выделения его из металлической ванны) может быть описан следующим уравнением [3]:
 H2 (г) = [H](в Fe) ; lgK = (-1900/T ) - 1,577. (9.33)
H2 (г) = [H](в Fe) ; lgK = (-1900/T ) - 1,577. (9.33)
Запишем выражение константы равновесия процесса (9.33) применительно к условиям данной задачи:
K = [H] 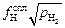 , (9.34)
, (9.34)
где рH2 - давление водорода в пузыре. Тогда искомая концентрация [H] равна
[H] = 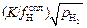 . (9.35)
. (9.35)
Величина рH2 в пузыре
рH2 = pocт + pgh + 2s/r, (9.36)
где pgh - ферростатическое давление (g - ускорение свободного падения, равное 9,8 м/с2).
Решение. Вычислим значение K: lgK = (-1900/1873) - 1,577 = = -2,59; K = 0,0026. Определим fH по параметрам взаимодействия (см. задачу 16); lg fH = 0,04; fH = 1,1. По формуле (9.36) вычислим рH2 в пузыре: рH2 = 4×102 + 7,0×103×9,8×0,5 + 2×1,68/(5×10-4)2 = 41420 Па » » 0,41 атм. По формуле (9.35) определим [H]:
[H] = (0,0026/1,1) 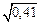 = 0,0015 %.
= 0,0015 %.
Таким образом, при вакуумировании ванны жидкой стали 30ХГСА глубиной 0,5 м водород может выделяться с пода в виде пузырей, если концентрация его в ванне [H] ³ 0,0015 %.
86. Удаление серы при обработке металла сульфидообразующими реагентами
Задача. Вычислить максимально возможную (равновесную) концентрацию серы в стали при обработке расплава карбидом кальция. Рассчитать науглероживание стали и минимально необходимый (теоретический) расход карбида кальция.
Исходные данные и рекомендуемые допущения. 1. Состав стали: 0,3 % С; 0,3 % Si; 0,4 % Mn. 2. Температура 1873 К. 3. Активности карбида кальция и образующегося сульфида принять равными 1.
4. Давление пара кальция принять равным 1 атм, что приблизительно соответствует условиям обработки стали порошком карбида кальция в струе инертного газа при атмосферном давлении.
Теория. Задача сводится к расчету равновесия реакции
СаС2 (т) + [S] = CaS(т) + 2[С]. (9.37)
Значение стандартной энергии Гиббса для этой реакции 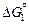 может быть найдено путем алгебраического суммирования DGº соответствующих реакций образования веществ из элементов (см. табл. П1) и реакций растворения элементов в жидком железе (см. табл. П2). Зная
может быть найдено путем алгебраического суммирования DGº соответствующих реакций образования веществ из элементов (см. табл. П1) и реакций растворения элементов в жидком железе (см. табл. П2). Зная 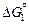 , определяем выражение для константы реакции (9.37):
, определяем выражение для константы реакции (9.37):
lg K = 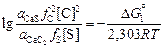 , (9.38)
, (9.38)
из которого вычислим равновесную концентрацию серы. Коэффициенты активности серы и углерода можно определить при помощи параметров взаимодействия (см. табл. П3). Для определения равновесной концентрации углерода в металле рассчитаем равновесие реакции
СаС2 (т) = Са(г) + 2[С]; DGº = -RT ln 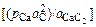 , (9.39)
, (9.39)
приняв заданные значения aCaC2 и рCa . Для определения минимально необходимого (теоретического) расхода карбида кальция, необходимо воспользоваться стехиометрическими соотношениями реакции (9.37), из которых следует, что для удаления 1 моля серы (32 г) требуется 1 моль СаС2 (64 г). В металл при этом переходят 2 моля углерода (24 г).
Решение. Определим равновесную концентрацию углерода в металле. Для определения DGo реакции (9.39) воспользуемся данными табл. П1 и П2:
СаС2 (т) = Са(г) + 2С(гр); DGº = 213000 - 61,0T Дж
2С(гр) = 2[С]; DGº = 45200 - 84,6Т Дж
СаС2 (т) = Са(г) + 2 [С]; DGº = 258200 - 145,6T Дж (9.40)
Из уравнения (9.40), приняв Т = 1873 К, aCaC2 = 1 и рCa = 1 атм, получим 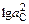 = (-258200 + 145,6×1873)/(19,14×1873) = 0,4045; аC = = 1,6 %. С помощью табл. П3 получим lg fC = 0,033; fC = 1,08, следовательно, [С] = аC /fC = 1,48 %. Полученный результат показывает, что десульфурация заданной стали карбидом кальция должна сопровождаться науглероживанием. Соотношение этих процессов определим ниже.
= (-258200 + 145,6×1873)/(19,14×1873) = 0,4045; аC = = 1,6 %. С помощью табл. П3 получим lg fC = 0,033; fC = 1,08, следовательно, [С] = аC /fC = 1,48 %. Полученный результат показывает, что десульфурация заданной стали карбидом кальция должна сопровождаться науглероживанием. Соотношение этих процессов определим ниже.
Для нахождения 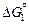 представим реакцию (9.37) как сумму следующих процессов:
представим реакцию (9.37) как сумму следующих процессов:
СаС2 (т) = Са(г) + 2С(гр); DGº = 213000 - 61,0T Дж (9.41)
[S] =  S2 (г); DGº = 72000 + 10,25Т Дж (9.42)
S2 (г); DGº = 72000 + 10,25Т Дж (9.42)
Са(г) +  S2 (г) = CaS(т); DGº = -692000 + 186,0Т Дж (9.43)
S2 (г) = CaS(т); DGº = -692000 + 186,0Т Дж (9.43)
2С(гр) = 2 [С]; DGº = 45200 - 84,6Т Дж (9.44)
СаС2 (т) + [S] = CaS(т) + 2[С]; 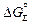 = -361800 + 50,65T Дж (9.45)
= -361800 + 50,65T Дж (9.45)
При 1873 К 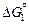 = -267000 Дж. Согласно выражению (9.38) с учетом равенства aCaC2 = aCaS = 1 получим
= -267000 Дж. Согласно выражению (9.38) с учетом равенства aCaC2 = aCaS = 1 получим 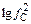 [С]2/fS [S] = -267000/(19,14×1873) =
[С]2/fS [S] = -267000/(19,14×1873) =
= 7,448. В соответствии с табл. П3 lg fS = 0,02; fS = 1,05.
Подставив найденные значения fC и fS в (9.39), получим
lg[(1,082×1,482)/(1,05×[S])] = 7,448; lg[S] = 7,448 + 2×0,033 + 2×0,17 -
- 0,02 = -7,067 [S] » 1×10-7 %.
Этот результат показывает, что десульфурация в рассматриваемых условиях может обеспечить очень низкий уровень концентрации серы в металле. Из приведенных выше стехиометрических соотношений видно, что удаление из металла каждой 0,01 % серы требует не менее 0,01×(64/32) = 0,02 % (0,2 кг/т) карбида кальция. При этом в металл переходит не менее 0,01×(24/32) = 0,0075 % углерода. Суммируя полученные результаты, можно сделать вывод, что карбид кальция является хорошим десульфуратором. Теоретически при расходе 0,2 кг карбида кальция на 1 т стали можно удалить 0,01 % серы при сравнительно небольшом науглероживании стали (на 0,0075 %). На практике в связи с угаром кальция и действием кинетических факторов, препятствующих достижению равновесия, расход карбида кальция и науглероживание должны быть выше.
87. Скорость удаления серы
из расплава в газовую фазу
Задача. Вычислить максимально возможную скорость десульфурации жидкой стали в результате испарения серы и образования серосодержащих газов при выдержке в вакууме и при обработке водородом.
Исходные данные и рекомендуемые допущения. 1. Масса расплава т = 1000 кг; состав: 0,1 % [С]; 0,02 % [S]; T = 1873 К. 2. Параметры вакуумной обработки: остаточное давление робщ = 1 Па (10-5 атм); производительность откачки 15×10–5 м3/с; [Н] = 0,0002 %. 3. Параметры обработки водородом: давление р = 101,325 кПа (1 атм), расход водорода 0,015 н×м3/с. 4. Принять, что максимальная скорость десульфурации соответствует насыщению газовой фазы серосодержащими газами (до их равновесных давлений). Концентрацию кислорода при вакуумной обработке определить из условия равновесия с углеродом при рCO = 10,1325 кПа (0,1 атм). При обработке водородом принять [О] = 0,0022 %.
Теория. Для решения задачи необходимо определить максимально возможное (равновесное) содержание серы в газовой фазе, а затем, по известной скорости газообмена, рассчитать максимально возможную скорость удаления серы из металла. Равновесное содержание серы в газовой фазе определяется термодинамическими характеристиками испарения серы и реакций образования серосодержащих газов: H2S, CS, CS2 , COS , SO2 и др. Эти характеристики могут быть определены по табл. П1 и П2. Результаты расчетов с использованием данных работ [9, 62] представлены в табл. 1 и для некоторых конкретных условий – на рисунке.
Таблица 1
Термодинамические характеристики реакций образования серосодержащих газов (по данным [9, 62], расчеты А.В. Богданова)
| Реакция | Коэффициенты в уравнении | |
| А | В | |
| 1. [S] = 1/2S2(г) | -3760 | -0,5355 |
| 2. [S] + 1/2Н2 (г) = HS(г) | -7718 | 0,2828 |
| 3. [S] + [H] = HS(г) | -5812 | 1,874 |
| 4. [S] + H2 = H2S(г) | 973 | -3,12 |
| 5. [S] + 2[H] = H2S(г) | 4786 | 0,066 |
| 6. [S] + [C] = CS(г) | -13672 | 1,845 |
| 7. 2[S] + [C] = CS2(г) | -5714 | -3,002 |
| 8. [S] + [C] + [0] = COS(г) | 2003 | -2,397 |
Окончание табл. 1
| Реакция | Коэффициенты в уравнении | |
| А | В | |
| 9. 2[S] + [O] = S2O(г) | -4731 | -4,510 |
| 10. [S] + [O] = SO(г) | -6803 | -0,426 |
| 11. [S] + 2[O] = SO2(г) | 2662 | -4,563 |
| 12. [S] + 3[O] = SO3(г) | 1528 | -9,450 |
| 13. [S] + [Si] = SiS(г) | -12908 | 2,735 |
| 14. 2[S] + [Si] = SiS2(г) | -8113 | -1,873 |
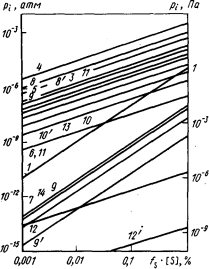
Равновесное давление серосодержащих газов pi (цифры на кривых соответствуют номерам в табл. 1, для сплавов на основе железа
при 1873 К) при разных расчетных условиях:
2, 4 - рH2 = 1 атм; 3, 5 - [Н] = 0,001 %; 6, 7 - [С] = 0,1 %;8 - [С] = 0,1 %;
[О] = 0,23 % (условно на поверхности металла); 8 - [С] = 0,1 %; [О] = 0,022 %;
9, 10, 11, 12 - [O] = 0,23 %; 9', 10', 11', 12' - [O] = 0,022 %; 13, 14 - [Si] = 0,1 %
В качестве примера расчетов, проведенных при построении графика, определим pH2S при T = 1873 К и [H] = 0,001 %.
По данным табл. 1
lg K = lg[pH2S /(aS[H]2)] = (4786/1873) + 0,066 = 2,621.
Отсюда
lg pH2S (атм) = 2,621 + 2lg(0,001) + lg aS = -3,379 + lg aS . (9.46)
Полученное уравнение соответствует прямой 5 на рисунке. Определив таким способом парциальные давления серосодержащих газов (р i) в заданных условиях, можно вычислить суммарную мольную долю серы в газовой фазе {S}S по формуле
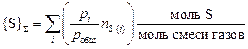 ,
,
где nS (i) - число атомов серы в молекуле газа i.
По известным значениям расхода газов, удаляемых из системы (q, н×м3/с), массы металла (m, г) и pобщ (Па) можно определить скорость десульфурации металла, %×с-1:
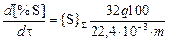 .
.
Решение. Коэффициент активности серы в заданном расплаве равен lg fS = -0,028×0,020 + 0,11×0,1 = 0,01044; fS = 1,024. Активность серы aS = 0,020×1,024 = 0,0205. Содержание кислорода при вакуумной обработке определим, приняв величину т = [% С]×[% О] =
= 0,0022×0,1 = 0,00022 (в 10 раз ниже, чем при атмосферном давлении, поскольку эффективное давление СО при вакуумной обработке обычно равно 0,1 атм). Получим [% О] = 0,00022/[% С] = 0,0022 %.
Равновесные давления серосодержащих газов (р i) находим с помощью уравнений табл. 1 или по рисунку (с корректировкой на более низкие содержания кислорода и водорода). Для обработки в атмосфере водорода получим
lg pH2S = lg K + lgaS + lg рH2 = 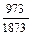 - 3,12 - 1,6882 + 0 = -4,2887;
- 3,12 - 1,6882 + 0 = -4,2887;
pH2S = 5,142×10-5 атм.
Скорости десульфурации в заданных условиях:
при обработке водородом
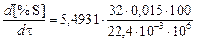 =
=
= 1,181×10-7 % ×с-1(0,00042 %×ч-1);
при вакуумной обработке
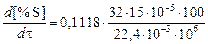 =
=
= 2,4×10-6 %×с-1(0,00864 %×ч-1).
Результаты расчетов значений р i , {S}i и {S}S приведены в табл. 2.
Таблица 2
Результаты расчетов значений р i , { S } i и { S } S
| Газ | Для атмосферы H2 | Для вакуума | ||
| р i ×105, атм | {S}i ×105 | р i ×105 aтм | {S} | |
| H2S | 5,142 | 5,142 | 0,0343 | 0,0343 |
| COS | 0,0514 | 0,0514 | 0,0514 | 0,0514 |
| HS | 0,2978 | 0,2978 | 0,0242 | 0,0242 |
| SO | 0,0004 | 0,0004 | 0,0004 | 0,0004 |
| CS | 0,0007 | 0,0007 | 0,0007 | 0,0007 |
| S2 | 0,0004 | 0,0008 | 0,0004 | 0,0008 |
| {S}S = 5,4931×10-5 | {S}S = 0,1118 | |||
Примечание. Размерность {S}å – моль S/моль смеси газов.
Примечание. Скорости десульфурации в реальных условиях внепечной вакуумной обработки и даже вакуумной плавки при указанных параметрах существенно ниже, так как равновесие между расплавом и газовой фазой не достигается вследствие кинетических условий, поэтому на практике рассмотренные процессы не применяют. Для удаления серы разработаны другие, более эффективные методы: обработка шлаками, продувка аргоном в смеси с порошками (извести, силикокальция, РЗМ и др.).
88. Раскислительная способность шлака
Задача. Рассчитать количество синтетического шлака, необходимое для рафинирования 1 т стали от кислорода при 1873 К.
Исходные данные. 1. Состав шлака: 50 % СаО; 50 % Аl2О3 2. [О]нач =
= 0,05 %; [О]кон = 0,005 %.
Теория. Шлак, находящийся в равновесии с металлом, содержит определенное количество FeO в соответствии с реакцией
[Fe] + [О] = (FeO), DGo = -120998 + 52,37T Дж/моль,
K = a(FeO) /a[Fe] a[O] . (9.47)
Если металл, отделенный от равновесного шлака, привести в контакт с новым шлаком, не содержащим FeO, то в результате реакции (9.47), понизится содержание кислорода в металле, а в шлаке появится FеО, т.е. произойдет раскисление металла шлаком.
Решение. Чтобы не усложнять примера, принимаем gFеO , f[O] и a[Fe] равными 1: K = х(FeO)/[% О], lnK = -DGo/RT; lnK = (14553/T ) – 6,3; K1873 К = 4,3.
К концу обработки равновесное содержание FeO в шлаке окажется равным xFeO = K [% О] = 4,3×0,005 = 0,0215 моль-1. Для этого из металла в шлак должно перейти кислорода: тO = [(0,05 - 0,005)×1000]/100 = 0,45 кг или FeO: mFeO = тOМFeO /МO = (0,45 – 72)/16 = 2,025 кг, где МFeO и МO - молекулярные массы FeO и кислорода. В 100 г исходного шлака (50 % СаО и 50 % Al2O3) содержится молей СаО и Al2O3 : nCaO = 50/56, nAl2O3 = 50/102. Соотношение nCaO /nAl2O3 = (50×102)/(56×50) = l,82 остается постоянным в процессе обработки металла. После обработки шлак содержит молей FeO: nFeO = 2025/72 = 28,125 молей.
Решая совместно систему уравнений
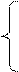 x =
x = 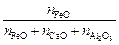 = 0,0215;
= 0,0215;
nCaO /nAl2O3 = 1,82;
nFeO = 28,125.
получим nCaO = 826,507 молей; nAl2O3 = 454,125 молей.
Масса шлака
mш = nFeO mFeO + nCaO mCaO + nAl2O3 mAl2O3 ,
mш = 2,026 + 826,607×0,056 + 454,125×0,102 = 94,6 кг
или 9,5 % от массы металла, что заметно превышает количество синтетического шлака в практике обработки стали в ковше (3,5–5 %).
89. Расчет равновесного состава металла
и шлака с применением ЭВМ
Задача. В ковш выпустили из ДСП-100 низкоуглеродистую сталь. Во время выпуска ее раскислили ферросилицием и алюминием. Для дополнительной десульфурации металла добавили известь. Определить количество и состав конечного металла и шлака, считая, что в системе устанавливается равновесие.
Исходные данные. 1. Жидкая сталь перед выпуском в ковш содержит 0,18 % [О], масса 100 т. 2. Ферросилиций ФС65 содержит 65 % Si, 35 % Fe, масса 0,1 т. 3. Алюминий вторичный АВ92, содержит 92 % Al, 8 % Si, масса 0,1 т. 4. Известь 100 % СаО, масса 0,3 т. 5. Температура 1873 К. 6. Валентности (степени окисления) элементов в шлаке считать постоянными, их значения: nFe = +2, nCa = +2, nSi = +4, nAl = +3, nO = -2. 7. Изменения энергий Гиббса образования соединений по реакциям
[Ме] + 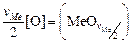 (9.48)
(9.48)
и выражения для определения констант равновесия химических реакций:
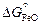 = -120850 + 23,3Т; (9.49) lgKFe = (6317/T ) - 1,22; (9.50)
= -120850 + 23,3Т; (9.49) lgKFe = (6317/T ) - 1,22; (9.50)
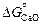 = -668230 + 165,1Т; (9.51) lgKCa = (34951/T ) - 8,63; (9.52)
= -668230 + 165,1Т; (9.51) lgKCa = (34951/T ) - 8,63; (9.52)
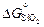 = -701550 + 140,6Т; (9.53) lgKSi = (36672/T ) - 7,35; (9.54)
= -701550 + 140,6Т; (9.53) lgKSi = (36672/T ) - 7,35; (9.54)
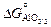 = -663810 + 121,9Т; (9,55) lgKAl = (34669/T ) - 6,37. (9.56)
= -663810 + 121,9Т; (9,55) lgKAl = (34669/T ) - 6,37. (9.56)
8. За стандартные состояния в пункте 7 приняты чистые жидкие металл и его оксид. Если их температуры плавления больше 1873 К, то стандартное состояние для условий задачи гипотетическое. Для кислорода за стандарт принят его гипотетический бесконечно разбавленный раствор в железе с х[O] = 1, т.е. при х[O] ® 0 коэффициент активности g[O] = 1, a[O] = х[O] (см. [3, с. 23–24]; g[O] в тексте – аналог j[O] в [3]).
Теория. Решение основано на сочетании материального баланса и термодинамического расчета. Термодинамический расчет позволяет установить составы фаз в равновесии.
Распределение i-го элемента по кислороду может быть представлено константой (см. задачу 24).
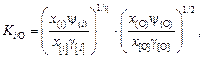 (9.57)
(9.57)
где ni - валентность (степень окисления) i-го элемента в фазе; х[i] , x(i) - атомные доли i-го элемента в металле и шлаке; g[i] - коэффициент активности в металле; y(i) - коэффициент активности в шлаке, рассчитываемый по модели коллективизированных электронов (МКЭ).
Однако в литературе не приводятся значения константы Ki/O . Чтобы использовать справочные данные по константам распределения, необходимо учесть переход от одного стандартного состояния (когда компонентом шлаковой фазы является элемент, как принято в МКЭ) к другому (когда компонент шлака - оксид).
Тогда получим выражение
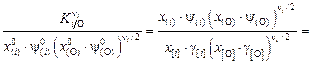
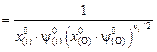 , (9.58)
, (9.58)
которое эквивалентно константе реакции (9.48):
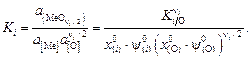 (9.59)
(9.59)
Значения константы Ki можно вычислить по температурной зависимости констант, приводимых в литературе (они собраны в пункте 7 исходных данных задачи). Атомные доли выразим через массы элементов
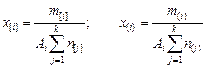 ; (9.60)
; (9.60)
где 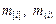 – массы i-го элемента в металле и шлаке;
– массы i-го элемента в металле и шлаке; 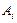 – атомная масса,
– атомная масса, 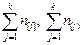 – суммы числа молей элементов, которые определяются следующим образом:
– суммы числа молей элементов, которые определяются следующим образом:
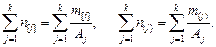 (9.61)
(9.61)
Учитывая выражение (9.60) и вводя обозначение
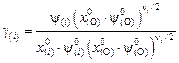 , (9.62)
, (9.62)
получим окончательное выражение
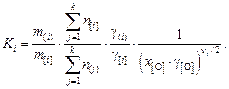 (9.63)
(9.63)
Алгоритм решения
1. Определение массы каждого элемента, поступившего в систему с исходными материалами по формуле
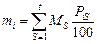 , (9.64)
, (9.64)
где 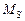 – масса S-гo исходного материала;
– масса S-гo исходного материала; 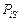 – процентное содержание i-го элемента в этом материале;
– процентное содержание i-го элемента в этом материале; 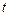 – общее число исходных материалов.
– общее число исходных материалов.
Например, кислород находится в стали 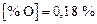 и в извести
и в извести 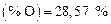 , тогда его масса равна
, тогда его масса равна
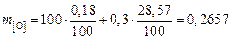 т.
т.
2. Составление и решение системы уравнений. В систему входят: балансовое уравнение (1), уравнение константы (2), уравнение электронейтральности (3):
|
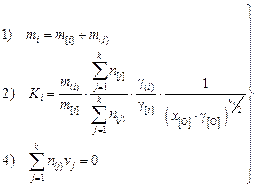 (9.65)
(9.65)
Система уравнений (9.65) решается методом итераций. Для этого необходимо задать начальные значения переменных. Вначале принимаем, что 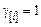 ,
, 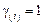 , задаем значение отношения
, задаем значение отношения 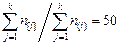 , эти величины уточняются в процессе итераций, поэтому их значения определяются лишь соображениями удобства. Задаемся также начальным значением окисленности металла, оно по условию задачи равно
, эти величины уточняются в процессе итераций, поэтому их значения определяются лишь соображениями удобства. Задаемся также начальным значением окисленности металла, оно по условию задачи равно 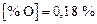 .
.
Вначале итерации ведутся на основе уточнения содержания кислорода в металле методом половинного деления. Указанное в условии задачи содержание кислорода принимается за верхнее значение интервала, за нижнее принимается 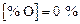 . Если решение находится в заданном интервале, то последующее значение определяется по формуле
. Если решение находится в заданном интервале, то последующее значение определяется по формуле
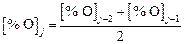 . (9.66)
. (9.66)
Атомная доля кислорода в металле определяется первоначально по формуле
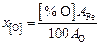 , (9.67)
, (9.67)
затем, после определения состава металла, она рассчитывается по формуле (9.60).
Критерием завершения итераций служит баланс по кислороду. Если не соблюдается неравенство
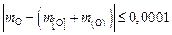 ,
,
то итерации повторяются, в противном случае переходят к дальнейшим вычислениям. По полученным значениям 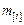 и
и 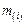 оцениваем по уравнению (9.61) суммы чисел молей в металле и шлаке. Затем рассчитываем общие массы металла и шлака и их состав в процентах.
оцениваем по уравнению (9.61) суммы чисел молей в металле и шлаке. Затем рассчитываем общие массы металла и шлака и их состав в процентах.
3. Вычисление коэффициентов активности компонентов. С помощью МКЭ вычисляем g(i) по формуле (9.62), учитывая стандартное состояние
i-го компонента. Рассчитываем g[i] с помощью параметров взаимодействия Вагнера. При этом приняли, что раствор является разбавленным, и тогда коэффициенты активности имеют постоянные значения: g[Fe] = 1; g[Ca] = 1; 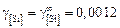 ;
; 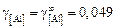 ;
; 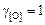 .
.
Затем вновь обращаемся к пункту 2, подставив в систему (9.65) новые значения 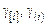 и приняв за нижнее значение
и приняв за нижнее значение 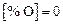 , а за верхнее – то, которое получилось в предыдущей итерации. Критерием окончания вычислений являются установившиеся значения составов металла и шлака.
, а за верхнее – то, которое получилось в предыдущей итерации. Критерием окончания вычислений являются установившиеся значения составов металла и шлака.
К решению прилагаются блок-схема алгоритма (см. рисунок), и результаты расчета (табл. 1 и 2). Описанный алгоритм можно использовать для моделирования любого сталеплавильного процесса или отдельных его периодов, когда известны составы и количества исходных материалов в начале периода.
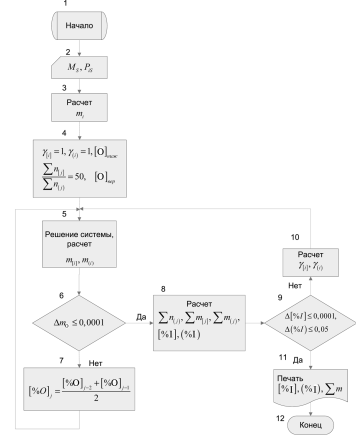
Блок-схема алгоритма расчета задачи 89
Таблица 1
Результаты расчета задачи 89
| Номер итерации по составу | Номер итерации по [O] | Массы элементов, т | Фаза | |||||
| Fe | Са | Si | Аl | O | 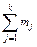
| |||
| 99,8550 | 0,2143 | 0,0730 | 0,0920 | 0,2657 | 100,5000 | 3 | ||
| 1 | 1 | 98,3007 | 0 | 0 | 0 | 0,1073 | 98,4780 | М |
| 1,5543 | 0,2143 | 0,0730 | 0,0920 | 0,6950 | 2,6285 | Ш | ||
| 2 | 99,0718 | 0 | 0 | 0 | 0,0892 | 99,1610 | М | |
| 0,7832 | 0,2143 | 0,0730 | 0,0920 | 0,4747 | 1,6372 | Ш | ||
| 3 | 99,4618 | 0 | 0 | 0 | 0,0448 | 99,5066 | М | |
| 0,3932 | 0,2143 | 0,0730 | 0,0920 | 0,3632 | 1,1357 | Ш | ||
| 4 | 99,5580 | 0 | 0 | 0 | 0,0224 | 99,6805 | М | |
| 0,1970 | 0,2143 | 0,0730 | 0,0920 | 0,3072 | 0,8834 | Ш | ||
| 5 | 99,7564 | 0 | 0 | 0 | 0,0112 | 99,7677 | М | |
| 0,0986 | 0,2143 | 0,0730 | 0,0920 | 0,2791 | 0,7569 | Ш | ||
| 6 | 99,8057 | 0 | 0,0001 | 0 | 0,0056 | 99,8114 | М | |
| 0,0493 | 0,2143 | 0,0729 | 0,0920 | 0,2649 | 0,6935 | Ш | ||
| 7 | 99,8303 | 0 | 0,0003 | 0 | 0,0028 | 99,8334 | М | |
| 0,0247 | 0,2143 | 0,0727 | 0,0920 | 0,2576 | 0,6613 | Ш | ||
| 8 | 99,8180 | 0 | 0,0001 | 0 | 0,0042 | 99,8224 | М | |
| 0,0370 | 0,2143 | 0,0729 | 0,0920 | 0,2613 | 0,6775 | Ш | ||
| 9 | 99,8118 | 0 | 0,0001 | 0 | 0,0049 | 99,8169 | М | |
| 0,0432 | 0,2143 | 0,0729 | 0,0920 | 0,2631 | 0,6855 | Ш | ||
| 10 | 99,8149 | 0 | 0,0001 | 0 | 0,0046 | 99,8196 | М | |
| 0,0401 | 0,2143 | 0,0729 | 0,0920 | 0,2622 | 0,6815 | Ш | ||
| 11 | 99,8165 | 0 | 0,0001 | 0 | 0,0044 | 99,8210 | М | |
| 0,0385 | 0,2143 | 0,0729 | 0,0920 | 0,2618 | 0,6895 | Ш | ||
| 12 | 99,8172 | 0 | 0,0001 | 0 | 0,1043 | 99,8217 | М | |
| 0,0378 | 0,2143 | 0,0729 | 0,0920 | 0,2616 | 0,6785 | Ш | ||
| 13 | 99,8176 | 0 | 0,0001 | 0 | 0,0043 | 99,8220 | М | |
| 0,0374 | 0,2143 | 0,0729 | 0,0920 | 0,2615 | 0,6780 | Ш | ||
| 2 | 1 | 99,7875 | 0 | 0,0040 | 0,0001 | 0,0043 | 99,7959 | М |
| 0,0675 | 0,2143 | 0,0690 | 0,0919 | 0,2655 | 0,7081 | Ш | ||
| 2 | 99,8213 | 0 | 0,0137 | 0,0004 | 0,0021 | 99,8375 | М | |
| 0,0337 | 0,2143 | 0,0593 | 0,0916 | 0,2446 | 0,6435 | Ш | ||
| 3 | 99,8044 | 0 | 0,0068 | 0,0002 | 0,0032 | 99,8146 | М | |
| 0,0506 | 0,2142 | 0,0662 | 0,0918 | 0,2574 | 0,6803 | Ш | ||
| 4 | 99,7960 | 0 | 0,0051 | 0,0002 | 0,0037 | 99,8050 | М | |
| 0,0590 | 0,2143 | 0,0679 | 0,0918 | 0,2638 | 0,6948 | Ш | ||
| 5 | 99,9717 | 0 | 0,0045 | 0,0002 | 0,0040 | 99,8004 | М | |
| 0,0633 | 0,2143 | 0,0685 | 0,0918 | 0,2637 | 0,7016 | Ш | ||
| 6 | 99,7939 | 0 | 0,0048 | 0,0002 | 0,0039 | 99,8027 | М | |
| 0,0611 | 0,2143 | 0,0682 | 0,0918 | 0,2628 | 0,6982 | Ш | ||
| 7 | 99,7949 | 0 | 0,0050 | 0,0002 | 0,0038 | 99,8038 | М | |
| 0,0601 | 0,2143 | 0,0680 | 0,0918 | 0,2623 | 0,6965 | Ш | ||
| 8 | 99,7954 | 0 | 0,0050 | 0,0002 | 0,0038 | 99,8844 | М | |
| 0,0596 | 0,2143 | 0,0680 | 0,0918 | 0,2620 | 0,6957 | Ш | ||
Окончание табл. 1
| 3 | 1 | 99,7926 | 0 | 0,0054 | 0,0002 | 0,0038 | 99,8019 | М |
| 0,0624 | 0,2143 | 0,0676 | 0,0918 | 0,2624 | 0,6985 | Ш | ||
| 2 | 99,8238 | 0 | 0,0177 | 0,0002 | 0,0019 | 99,8438 | М | |
| 0,0312 | 0,2143 | 0,0553 | 0,0918 | 0,2392 | 0,63l6 | Ш | ||
| 3 | 99,8082 | 0 | 0,0091 | 0,0002 | 0,0028 | 99,8204 | М | |
| 0,0468 | 0,2143 | 0,0639 | 0,0918 | 0,2537 | 0,6704 | Ш | ||
| 4 | 99,8004 | 0 | 0,0069 | 0,0002 | 0,0033 | 99,8108 | М | |
| 0,0546 | 0,2143 | 0,0661 | 0,0918 | 0,2584 | 0,6852 | Ш | ||
| 5 | 99,7965 | 0 | 0,6061 | 0,0002 | 0,0035 | 99,8063 | М | |
| 0,0585 | 0,2143 | 0,0669 | 0,0918 | 0,2605 | 0,6920 | Ш | ||
| 6 | 99,7945 | 0 | 0,0057 | 0,0002 | 0,0036 | 99,8041 | М | |
| 0,0605 | 0,2143 | 0,0673 | 0,0918 | 0,2615 | 0,6953 | Ш | ||
| 7 | 99,7936 | 0 | 0,0056 | 0,0002 | 0,0037 | 99,8030 | М | |
| 0,0614 | 0,2143 | 0,0674 | 0,0918 | 0,2620 | 0,6969 | Ш | ||
| 4 | 1 | 99,7932 | 0 | 0,0056 | 0,0002 | 0,0037 | 99,8027 | М |
| 0,0618 | 0,2143 | 0,0674 | 0,0918 | 0,2620 | 0,6973 | Ш |
Таблица 2
Состав металла (числитель) и шлака (знаменатель), % масс.
| Номер итерации по составу | 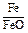
| 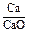
| 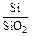
| 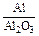
| 
| 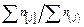
|
| 1 | 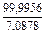
| 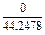
| 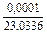
| 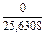
| 0,0043 | 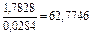
|
| 2 | 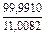
| 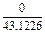
| 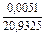
| 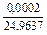
| 0,0038 | 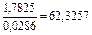
|
| 3 | 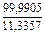
| 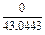
| 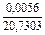
| 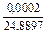
| 0,0037 | 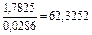
|
| 4 | 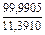
| 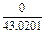
| 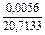
| 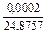
| 0,0037 | 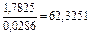
|
90. Расчет распределения элементов
переменной валентности между металлом
и шлаком с применением ЭВМ
Задача. Подшипниковую сталь обрабатывают в вакууме под синтетическим шлаком состава 40 % CaO, 30 % SiO2 , 30 % Аl2О3 . Рассчитать равновесное содержание железа в шлаке и его валентность при различном общем давлении в системе: 1; 0,1; 0,01; 0,001; 0,0001; 0,00001 атм, пренебрегая восстановлением компонентов шлака углеродом, содержащимся в стали, пользуясь классической моделью (законом действующих масс) и МКЭ.
Исходные данные. 1. Состав стали: 1,0 % С; 0,27 % Si; 0,30 % Mn; 0,027 % Р; 0,020 % S; 1,52 % Сr; 0,30 % Ni. 2. Параметры взаимодействия 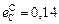 ;
; 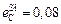 ;
; 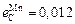 ;
; 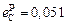 ;
; 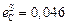 ;
; 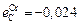 ,
, 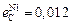 . 3. Давление СО в системе равно общему давлению. 4. Термодинамические характеристики реакции окисления углерода:
. 3. Давление СО в системе равно общему давлению. 4. Термодинамические характеристики реакции окисления углерода:
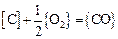 ;
; 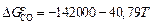 ;
; 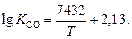
5. Термодинамические характеристики реакции образования оксида железа (II):
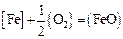 ;
; 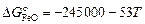 ;
; 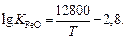
6. Температурные зависимости параметров 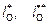 для определения валентности железа
для определения валентности железа 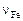 :
:
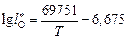 ;
; 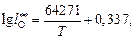
где 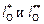 – коэффициенты распределения кислорода между фазами1.
– коэффициенты распределения кислорода между фазами1.
7. Температурная зависимость константы интегрирования:
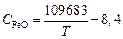 .
.
8. Стандартные состояния: для углерода – 1 %-ный раствор в железе, для железа и оксида железа – чистые жидкие вещества.
Теория. Обычно при описании распределения элементов исходят из уравнения реакции и соответствующего ей выражения закона действующих масс:
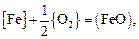
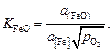 (9.68)
(9.68)
Этот путь является строгим лишь в том случае, если валентность элементов (в нашем случае кислорода и железа) остается постоянной в рамках решаемой задачи. Валентность кислорода в металлургических шлаках действительно постоянна и равна 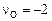 . Валентность железа изменяется в зависимости от окислительно-восстановительного потенциала системы и состава шлака. Значение
. Валентность железа изменяется в зависимости от окислительно-восстановительного потенциала системы и состава шлака. Значение 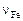 может непрерывно изменяться в диапазоне
может непрерывно изменяться в диапазоне 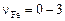 .
.
Равновесие элементов описывается дифференциальным уравнением распределения их между фазами
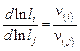 , (9.69)
, (9.69)
где 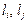 – коэффициенты распределения i-го и j-го элементов между фазами,
– коэффициенты распределения i-го и j-го элементов между фазами, 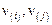 – их валентности в шлаке.
– их валентности в шлаке.
Коэффициент распределения i-го элемента между фазами определяется по формуле
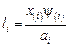 , (9.70)
, (9.70)
где 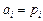 , если шлак контактирует с газом и
, если шлак контактирует с газом и 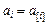 , если шлак контактирует с металлом.
, если шлак контактирует с металлом.
Из выражения (9.70) получается дифференциальное уравнение:
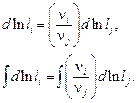 (9.71)
(9.71)
При постоянных 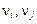 уравнение (9.71) переходит в выражение закона действующих масс. Действительно, после интегрирования (9.71) получим, что отношение
уравнение (9.71) переходит в выражение закона действующих масс. Действительно, после интегрирования (9.71) получим, что отношение 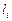 и
и 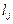 является постоянной величиной.
является постоянной величиной.
Зависимость 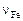 от
от 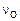 , полученная на основе МКЭ с помощью квантовой статистики Ферми – Дирака, имеет вид
, полученная на основе МКЭ с помощью квантовой статистики Ферми – Дирака, имеет вид
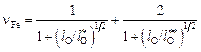 . (9.72)
. (9.72)
Выражение (9.72) определяет валентность как среднюю статистическую степень заселенности электронных уровней (3d и 4s) железа в шлаке. Константы 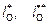 соответствуют уровням 3d и 4s соответственно. На основании выражений (9.71) и (9.72), учитывая, что
соответствуют уровням 3d и 4s соответственно. На основании выражений (9.71) и (9.72), учитывая, что 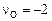 , имеем
, имеем
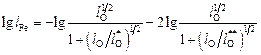 . (9.73)
. (9.73)
Алгоритм решения
1. Определение активности углерода в металле с помощью параметров взаимодействия по формулам
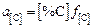 ;
; 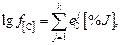 (9.74)
(9.74)
где 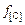 – коэффициент активности углерода в металле. Численное значение активности углерода для приведенных исходных условий
– коэффициент активности углерода в металле. Численное значение активности углерода для приведенных исходных условий 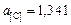 (для контроля).
(для контроля).
2. Определение давления кислорода
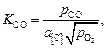
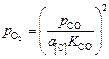 . (9.75)
. (9.75)