8. Неметаллические включения в стали
71. Расчет массовой и объемной доли включений, выделившихся в металле
при его охлаждении до данной температуры
Задача. Определить при данной температуре массовую и объемную доли нитридов титана в железе при введении титана в металл с заданной концентрацией азота.
Исходные данные
1. Расчетная температура 1823 К.
2. Исходная концентрация азота (суммарный азот в металле) 0,01 %.
3. В металл присаживается 0,5 % Ti.
4. Плотность жидкого железа 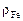 = 7000 кг/м3.
= 7000 кг/м3.
5. Плотность нитрида титана 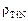 = 5430 кг/м3.
= 5430 кг/м3.
Теория. Включения типа 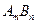 диссоциируют в металле по реакции
диссоциируют в металле по реакции
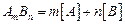 ,
,
где 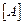 и
и 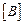 – концентрации растворенных компонентов.
– концентрации растворенных компонентов.
Константа равновесия этой реакции
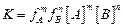 , (8.1)
, (8.1)
где 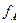 и
и 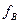 – коэффициенты активности компонентов A и B.
– коэффициенты активности компонентов A и B.
Если включения растворены не полностью, то суммарное содержание компонентов A и B в системе металл – включения должно учитывать как растворенные компоненты, так и компоненты, связанные в соединение 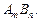
Обозначим общее содержание компонентов в металле через 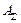 и
и 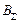 , а концентрации, отвечающие их связанным долям, через
, а концентрации, отвечающие их связанным долям, через 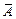 и
и 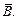 Тогда в любой момент имеем
Тогда в любой момент имеем 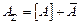 и
и 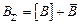 , или
, или
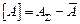 и
и 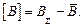
Величины 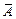 и
и 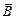 связаны между собой стехиометрическими соотношениями
связаны между собой стехиометрическими соотношениями 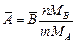 ,
,
где МА и МВ – атомные массы компонентов A и B соответственно.
Отсюда имеем соотношения между концентрациями растворенных компонентов: 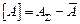 =
= 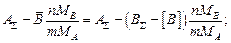
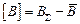 =
= 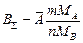 =
= 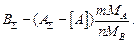
Подставив эти соотношения в выражение для константы, получим
K= 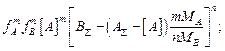 (8.2)
(8.2)
K= 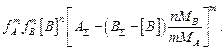 (8.3)
(8.3)
В обоих этих выражениях при заданных значениях 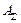 ,
, 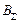 и К мы имеем только одно неизвестное – либо [A], либо [B], относительно которых их надо решать. Однако сложность решения этих уравнений заключается, во-первых, в том, что показатели m и n могут отличаться от 1, во-вторых, коэффициенты активности
и К мы имеем только одно неизвестное – либо [A], либо [B], относительно которых их надо решать. Однако сложность решения этих уравнений заключается, во-первых, в том, что показатели m и n могут отличаться от 1, во-вторых, коэффициенты активности 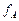 и
и 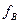 сами зависят от концентрации растворенных компонентов [A] и [B]:
сами зависят от концентрации растворенных компонентов [A] и [B]:
lg 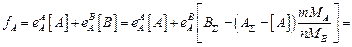
= 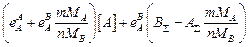 ;
;
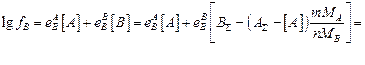
= 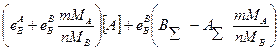
или, выразив 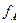 и
и 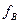 через [B], получим
через [B], получим
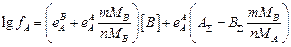 ;
;
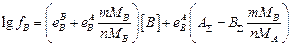 .
.
Поэтому в общем случае уравнения (8.2) и (8.3) надо решать методом итераций и лучше всего с использованием ЭВМ.
В случае, когда m = n = 1, задача несколько упрощается и уравнения (8.2) и (8.3) принимают вид
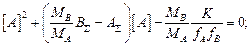 (8.4)
(8.4)
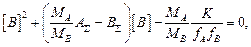 (8.5)
(8.5)
где lg 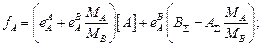
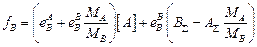
или 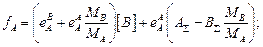
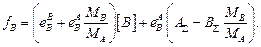
Если одна из величин [A] и [B] достаточно мала, чтобы ее влиянием на коэффициенты активности можно было пренебречь, уравнения (8.4) и (8.5) превращаются в обычные квадратные уравнения. При решении задачи необходимо, прежде всего, выбрать, относительно какого растворенного элемента ( 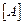 и [B]) ее следует решать.
и [B]) ее следует решать.
Допустим, что выбран элемент А. Найдя величину [A], находим связанный элемент 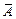 :
: 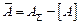 .
.
Затем находим связанный элемент 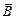 :
: 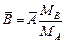 .
.
Теперь можно найти концентрацию элемента В в растворе: 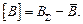
Массовая доля соединения 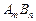 в металле
в металле
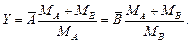
Объемная доля включений при этом составит 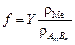 ,
,
где 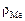 и
и 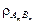 – соответственно плотности металла и соединения.
– соответственно плотности металла и соединения.
Решение. На основании справочных данных примем в железе для реакции диссоциации TiN
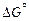 = 291180 – 107,96 Т Дж/моль;
= 291180 – 107,96 Т Дж/моль;
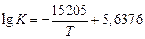 ;
;
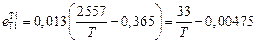 ;
; 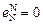 ;
;
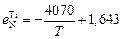 ;
; 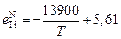 .
.
Найдем температуру начала образования нитрида при охлаждении металла (при нагреве – начала его разложения) из условия: 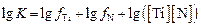 .
.
Если титан и азот целиком находятся в растворе, то
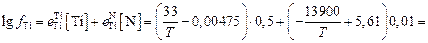
= 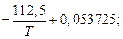
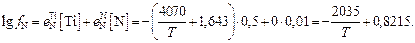
Тогда при Т = Тнач имеем
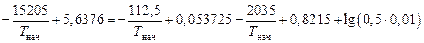
или 
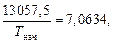 откуда Тнач = 1848,6 К.
откуда Тнач = 1848,6 К.
Таким образом, Тнач выше температуры процесса, и в жидком железе должен идти процесс образования нитрида TiN.
При Т = 1823 К имеем:
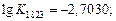
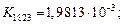
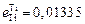 ;
; 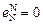 ;
; 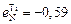 ;
; 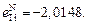
Примем в расчетах, что элемент А – это титан, а элемент В – азот, и возьмем в качестве опорного неизвестного растворенный азот.
Тогда при условии, что m = n = 1, необходимое уравнение примет вид
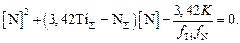
При заданных значениях 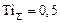 % и
% и 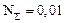 % имеем
% имеем
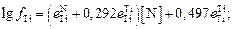
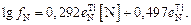
При Т = 1823 К получим
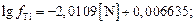
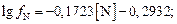
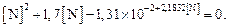
Решение методом итераций дает 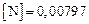 %.
%.
Количество азота, связаного в нитрид, 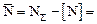 0,01 –
0,01 –
– 0,00797 = 0,00203 %.
Количество титана, связаного в нитрид, 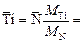
= 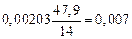 %.
%.
В растворе находится титана 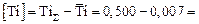
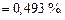
Массовая доля образовавшихся нитридов составляет величину
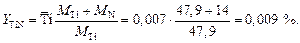
Объемная доля нитридов
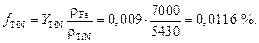
72. Влияние размеров частиц и объемной
доли неметаллической фазы на размер зерна
и механические свойства металла
Задача. Определить влияние размеров частиц неметаллических включений (d) и их объемной доли в металле (f) на размер зерна аустенита и условный предел текучести ( 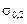 ) сталей типа 03X18H10 и 12X18H12T при 20 °C.
) сталей типа 03X18H10 и 12X18H12T при 20 °C.
Исходные данные. В обоих случаях для абсолютно чистой по н.в. металлической матрице принять при 20 °C 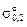 = 180 МПа, модуль Гука G = 7,78×10
= 180 МПа, модуль Гука G = 7,78×10 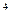 МПа, коэффициент Пуассона υ = 0,297, модуль вектора Бюргерса b = 0,356 нм.
МПа, коэффициент Пуассона υ = 0,297, модуль вектора Бюргерса b = 0,356 нм.
Принять, что:
– в стали без титана в основном присутствуют включения (оксиды, оксисульфиды, нитриды), образовавшиеся в жидком и жидко-твердом металле. Их средний размер d1 = 5 мкм (5×10–6м) при общей объемной доле частиц f1 = 10–3 (0,1 %);
– в стали с титаном кроме этих включений дополнительно имеются карбиды и карбонитриды титана, образовавшиеся в твердом металле и имеющие средний размер d2 = 5×10–7 м (0,5 мкм) и объемную долю f2 = 10–2 (1%);
– в сталь типа 03X18H10 с целью получения карбидостали дополнительно введены частицы карбида титана с размерами d3 = 5 мкм (5×10–6 м) и объемной долей f3 = 0,5 (50 %).
Определить: величину 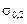 и средний размер зерна аустенита D для всех трех вариантов.
и средний размер зерна аустенита D для всех трех вариантов.
Теория. Неметаллические включения сложным образом влияют на механические свойства металла. Три механизма воздействия являются важнейшими[1]:
1) уменьшение «живого сечения» металла;
2) препятствие движению дислокаций при деформации металла;
3) блокирование роста зерна, если включения расположены по границам зерен.
Первый фактор уменьшает прочность металла, два других – повышают.
Обозначим условный предел текучести для чистой матрицы через 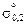 , а для системы «металл – н.в.» через
, а для системы «металл – н.в.» через 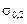 .
.
Тогда в общем случае 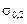 =
= 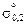 +
+ 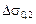 ,
,
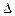
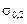 =
= 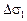 +
+ 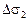 +
+ 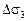 ,
,
где 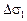 ,
, 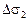 ,
, 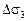 – соответственно изменения
– соответственно изменения 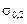 по трем приведенным выше механизмам.
по трем приведенным выше механизмам.
Если бы упрочнение по второму и третьему механизмам отсутствовало, то мы бы имели только разупрочнение металла при введении в него н.в.: 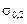 =
= 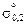 (1 – f) и
(1 – f) и 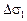 = –f
= –f 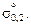
Для случая чистого дислокационного упрочнения изменение 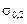 обозначим через
обозначим через 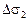 .
.
По модели Орована – Эшби 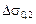 =
= 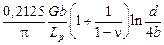 ,
,
где G – модуль Гука матрицы;
b – модуль вектора Бюргерса, численно равный параметру кристаллической решетки матрицы;
d – средний размер частиц второй фазы;
Lp – среднее расстояние между поверхностями частиц второй фазы;
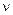 – коэффициент Пуассона.
– коэффициент Пуассона.
По модели Уилкокса – Клауэра Lp = d 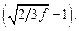
По модели Брауна и Хэма Lp = d 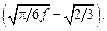
По обеим моделям при некотором критическом значении f = fкр Lp = 0 и 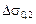
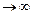 , т.е. при f ³ fкр модель дислокационного упрочнения теряет физический смысл. По Уилкоксу и Клауэру fкр = 2/3, а по Брауну и Хэму fкр =
, т.е. при f ³ fкр модель дислокационного упрочнения теряет физический смысл. По Уилкоксу и Клауэру fкр = 2/3, а по Брауну и Хэму fкр = 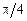 = 0,7854. Реальные значения fкр находятся где-то между этими двумя оценками. С учетом зависимости Lp от d для
= 0,7854. Реальные значения fкр находятся где-то между этими двумя оценками. С учетом зависимости Lp от d для 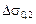 мы имеем
мы имеем
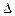
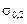 ~
~ 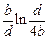 ,
,
т.е. функция 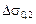 от
от 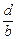 отрицательна при
отрицательна при 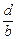 < 4, затем проходит через максимум при
< 4, затем проходит через максимум при 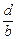 = 4eb
= 4eb 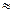 10,9b и затем асимптотически стремится к нулю при бесконечно большом значении
10,9b и затем асимптотически стремится к нулю при бесконечно большом значении 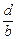 .
.
Границы зерен дополнительно упрочняют металл, и 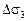 = K/ D1/2, где D – средний размер зерна.
= K/ D1/2, где D – средний размер зерна.
При 20 °С для железа и никеля К 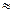 0,25–0,3 МПа×м1/2.
0,25–0,3 МПа×м1/2.
В свою очередь, величина D определяется блокирующим действием неметаллических включений.
По модели Зинера D = 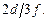
По модели Хеллмана – Хиллерта D = 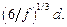
Решение
1. В стали присутствуют только частицы, возникшие в жидком и жидко-твердом металле.
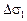 = –f1
= –f1 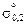 = –1×10–3×180 = – 0,18 МПа.
= –1×10–3×180 = – 0,18 МПа.
По модели Уилкокса – Клауэра
Lp = d 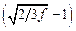 =5×10–6
=5×10–6 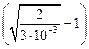 =1,24×10–4м;
=1,24×10–4м;
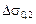 =
= 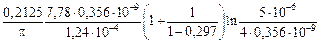 = 0,297 МПа.
= 0,297 МПа.
По модели Зинера, принимая К = 0,25 МПа×м1/2, имеем
D = 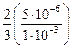 = 3,333×10–3 м;
= 3,333×10–3 м;
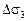 =
= 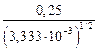 = 4,333 МПа.
= 4,333 МПа.
По модели Хеллмана – Хиллерта
D = 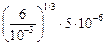 = 9,09×10–5 м;
= 9,09×10–5 м;
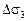 =
= 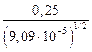 = 26,2 МПа.
= 26,2 МПа.
Принимаем полученные значения D и 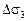 и имеем:
и имеем:
по Зинеру 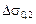 = –0,18 + 0,297 + 4,33 = 4,447 МПа,
= –0,18 + 0,297 + 4,33 = 4,447 МПа,
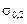 = 180 + 4,447 = 184,447 МПа;
= 180 + 4,447 = 184,447 МПа;
по Хелману – Хиллерту
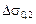 = –0,18 + 0,297 + 26,2 = 26,317 МПа,
= –0,18 + 0,297 + 26,2 = 26,317 МПа,
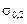 = 180 + 26,317 = 206,32 МПа.
= 180 + 26,317 = 206,32 МПа.
2. В стали с титаном присутствуют карбиды и карбонитриды, возникшие в твердом металле:
f = f1 + f2 = 1×10-3+1×10–2 = 1,1×10–2;
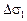 = – f
= – f 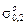 = –1,1×10–2×180 = –1,8 МПа.
= –1,1×10–2×180 = –1,8 МПа.
Средний размер частиц
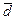 =
= 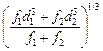 = 2,256×10–6 м = 2,256 мкм.
= 2,256×10–6 м = 2,256 мкм.
Среднее планарное расстояние между частицами разных размеров определяется по Уилкоксу – Клауэру по формуле
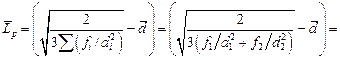
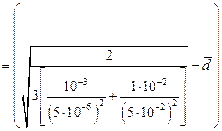 =1,824×10-6 м;
=1,824×10-6 м;
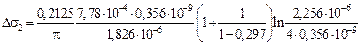 =
=
=18,2 МПа.
По модели Зинера
D = 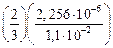 =1,367×10-4 м = 1,367 мкм;
=1,367×10-4 м = 1,367 мкм;
D 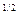 = 1,17×10-2 м1/2;
= 1,17×10-2 м1/2;
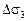 =
= 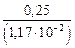 =21,38 МПа.
=21,38 МПа.
По модели Хеллмана – Хиллерта
D = 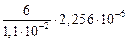 = 28,2 мкм;
= 28,2 мкм;
D1/2 = 5,31×10–3 м1/2;
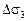 =
= 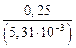 = 47,08 МПа.
= 47,08 МПа.
Принимаем значения 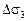 и D и имеем:
и D и имеем:
по Зинеру 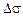 = –1,8 + 18,2 + 21,38 = 37,78 МПа;
= –1,8 + 18,2 + 21,38 = 37,78 МПа;
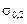 = 180 + 37,78 = 217,78 МПа.
= 180 + 37,78 = 217,78 МПа.
по Хеллману – Хиллерту 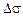 = –1,8 + 18,2 + 47,08 = 63,48 МПа;
= –1,8 + 18,2 + 47,08 = 63,48 МПа;
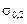 = 180 + 63,48 = 240,48 МПа.
= 180 + 63,48 = 240,48 МПа.
3. В карбидостали имеем по условию:
f = f1 + f3 = 1×10–3 + 0,5 = 0,501;
d = d1 + d3 = 5×10–6 м;
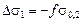 = –0,501×180 = –90,18 МПа;
= –0,501×180 = –90,18 МПа;
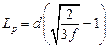 =5×10-6
=5×10-6 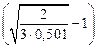 = 7,677×10–7 м;
= 7,677×10–7 м;
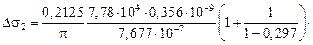
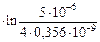 = 1838,8 МПа.
= 1838,8 МПа.
По модели Зинера D = 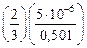 = 6,66 мкм;
= 6,66 мкм;
D1/2 = 2,58×10–3 м1/2;
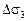 =
= 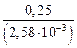 = 96,8 МПа.
= 96,8 МПа.
По модели Хеллмана – Хиллерта D = 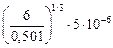 = 11,44 мкм;
= 11,44 мкм;
D1/2 = 3,382×10–3 м1/2;
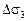 =
= 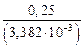 = 73,92 МПа.
= 73,92 МПа.
Принимаем полученные значения 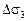 и D и имеем:
и D и имеем:
по Зинеру 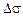 = –90,18 + 1838,8 + 96,8 = 1845,42 МПа;
= –90,18 + 1838,8 + 96,8 = 1845,42 МПа;
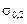 = 180 + 1845,42 = 2025,42 МПа;
= 180 + 1845,42 = 2025,42 МПа;
по Хеллману – Хиллерту 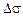 = –90,18 + 1838,8 + 73,92 = 1822,54 МПа,
= –90,18 + 1838,8 + 73,92 = 1822,54 МПа,
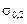 = 180 + 1822,54 = 2002,54 МПа.
= 180 + 1822,54 = 2002,54 МПа.
73. Удаление неметаллических включений
под действием гравитационных сил
Задача. Рассчитать скорости всплывания неметаллических частиц в стали при 1873 К в гравитационном поле (конвективное перемешивание металла не учитывать).
Исходные данные. 1. Плотность глинозема rв = 3,97×103 кг/м3, жидкой при 1873 К силикатной частицы 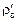 = 2,5×103 кг/м3, стали
= 2,5×103 кг/м3, стали
rм = 7,15×103 кг/м3 ; температура плавления глинозема 2288 К. 2. Вязкость стали при 1873 К hм = 6×10-3 Па×с, силикатной системы
hв = 5×10-1 Па×с. 3. Размеры включений 10, 20 и 50 мкм.
Теория. Скорость подъема твердых сферических частиц в спокойной жидкости (Re < 1) определяется уравнением Стокса:
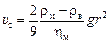 , (8.6)
, (8.6)
где r - радиус частиц; rм и rв - плотность вещества среды и включения соответственно; hм - динамическая вязкость среды; g - ускорение свободного падения.
Эта формула получена приравниванием выталкивающей силы, действующей на частицу (сила Архимеда), и силы сопротивления движению в вязкой среде:
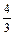 pr3g(rм – rв) = 6prhмυ.
pr3g(rм – rв) = 6prhмυ.
Формула Стокса обычно применима вплоть до Re = 1. Поведение частиц размером менее 10-7 м (0,1 мкм) подчиняется преимущественно закономерностям броуновского движения. Скорость подъема жидких и газообразных сферических частиц в однокомпонентной жидкости определяется уравнением Рыбчинского – Адамара, полученного решением системы соответствующих дифференциальных уравнений:
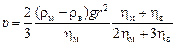 , (8.7)
, (8.7)
где hв - вязкость вещества частицы.
Очевидно, что для твердой частицы (hв >> hм) уравнение (8.7) переходит в формулу Стокса.
Решение. В случае всплывания твердых (при 1873 К) включений глинозема (Аl2О3) можно воспользоваться формулой (8.6). Частицы глинозема в металле, как правило, не имеют округлой формы, отклонение формы включений от сферической может заметно влиять на скорость их подъема. В случае одинакового объема наименьшее сопротивление испытывают округлые частицы. Для включений неправильной формы в знаменатель уравнения (8.6) вводят поправочный коэффициент k, равный для частиц А12О3 примерно 6 [50].
Далее будет показано, в каком интервале скоростей движения включения размером 5×10-5 м (50 мкм) в спокойном металле выполняется формула (8.6), т.е. Re = (υ drм)/hм £ 1, где d - характеристический размер, равный диаметру частицы,
υ £ (Rehм)/(rмd) = (1×6×10-3)/(7,15×103×5×10-5) = 1,6×10-2 м/с. (8.8)
Скорость подъема частицы глинозема размером 10 мкм
υ = 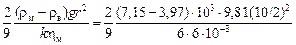 = 0,5×10-5 м/с.
= 0,5×10-5 м/с.
В соответствии с неравенством (8.8) полученное значение скорости удовлетворяет условию Re < 1, и для частиц такого размера можно применять уравнение Стокса. Аналогичным образом подсчитываем скорости всплывания частиц размером 20 и 50 мкм, равные соответственно 0,2×10-4 и 1,3×10-4 м/с.
Рассчитаем теперь скорость всплывания жидкого (при 1873 К) силикатного включения размером 10 мкм по формуле (8.7):
υ = 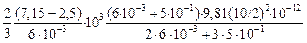 = 4×10-5 м/с.
= 4×10-5 м/с.
Для частиц размерами 20 и 50 мкм по уравнению (8.7) получим соответственно скорости всплывания, равные 1,6×10-4 и 1×10-3 м/с. В случае силикатного включения hв >> hм и поправочный множитель в уравнении Рыбчинского – Адамара примерно равен 1/3, поэтому формула (8.7) переходит в формулу (8.6). Проведенный расчет показывает, что жидкие силикатные включения в спокойном металле всплывают несколько быстрее твердых частиц глинозема, что связано с их меньшей плотностью и сферической формой.
Примечание. В металлургических агрегатах в условиях интенсивного перемешивания металла доставка неметаллических включений к поверхности ванны осуществляется преимущественно конвективными потоками. Гравитационные силы в основном играют роль при переходе частиц через тонкий слой металла, непосредственно прилегающий к границе раздела металл–шлак, где вертикальная составляющая скорости конвективных потоков практически равна нулю.
74. Влияние конвективных потоков
на удаление неметаллических включений
Задача. Сопоставить вклады конвективных потоков и всплывания частиц по закону Стокса в процесс рафинирования стали от неметаллических включений при выдержке в ковше и выплавке металла в индукционной печи.
Исходные данные. 1. Скорости конвективных потоков металла: в ковше υ = 0,5 м/с, в индукционной печи υ = 3 м/с. 2. Вязкость стали при 1873 К hм = 4×10-3 Па×с. 3. Плотность жидкой стали r = = 7,1×103 кг/м3, включений глинозема rв = 3,97×103 кг/м3. 4. Радиусы зеркала металла в ковше l = 1 м, тигля индукционной печи 0,5 м.
Теория. Удаление неметаллических включений в неперемешиваемом расплаве происходит только путем их всплывания. Тогда концентрация частиц в стали с изменяется в зависимости от времени по логарифмическому закону [51]
ln (с0/с) = (υct)/h = Кct, (8.9)
где с0 - исходная концентрация включений; h - глубина металлической ванны; υc - скорость всплывания включений по формуле Стокса (см. задачу 73); KС - константа Стокса.
В условиях интенсивного перемешивания металла конвективные потоки обеспечивают доставку частиц к границе раздела металл–шлак, и в этом случае зависимость концентрации неметаллических включений в расплаве от времени описывается уравнением [51]
ln(с0/с) = (2υ r/lh)t = Kконвt, (8.10)
где υ - скорость конвективных потоков в ванне; l - радиус зеркала металла; r - средний радиус включений; Kконв - константа конвективного перемешивания.
Решение. По условию задачи необходимо сопоставить величины Kконв = 2υ r /(lh) и KС = υС/h, определяющие удаление включений соответственно с конвективными потоками и в гравитационном поле.
При
r * = (9υhмk)/[l((rм - rв)gr2h]
отношение
Kконв/KС = (2υ r khмh)/[2/9(rм - rв)gr2h] = 1.
Если r > r *, то включения удаляются преимущественно в результате всплывания, при r < r * - выносом с конвективными потоками. В ковше для глиноземных включений
r = (9×0,5×5×10-3×6)/[1×(7,1 - 3,97)×103×9,81] » 5×10-6 м = 5 мкм.
Таким образом, расчет показывает, что частицы размером более 5×10-6 м (5 мкм) удаляются в основном в результате всплывания, а более мелкие - с конвективными потоками. В индукционной печи, где скорость конвективных потоков существенно выше,
r * = (9×3×5×10-3×6)/[0,5(7,1 - 3,97)×103×9,81] = 5,4×10-5 м = 54 мкм,
т.е. в этом агрегате основная масса включений удаляется преимущественно с конвективными потоками.
Примечание. Укрупнение частиц в объеме расплава, а также их затягивание с поверхности в объем ванны жидкого металла в рассматриваемой задаче не учитывались.
75. Поведение включений
в циркуляционных потоках металла
Задача. Рассчитать, при каких скоростях конвективных потоков в индукционной печи возможно затягивание неметаллических включений с поверхности в объем ванны жидкого металла.
Исходные данные. Диаметр тигля индукционной печи вместимостью 4 т D = 0,88 м. Схема перемешивания металла в индукционной печи представлена на рис. 1.
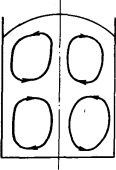 Рис. 1. Схема перемешивания металла в индукционной печати
Рис. 1. Схема перемешивания металла в индукционной печати
| 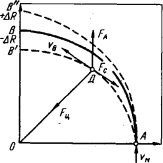 Рис. 2. Поведение включений в циркуляционных потоках металла
Рис. 2. Поведение включений в циркуляционных потоках металла
|
Теория. Включение, попавшее в циркуляционный поток металла в точке Д (рис. 2), под действием выталкивающей силы (силы Архимеда) FА , центростремительной силы Fц и сопротивления движению в вязкой среде Fс, отклоняется от траектории потока АВ, и на линии O В это отклонение составит ±DR, т.е. включение может либо затягиваться вглубь металла (при DR < 0), либо выталкиваться из потока (при DR > 0).
Соответствующие силы равны:
FА = 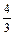 pr 3(rм - rв)g; (8.11)
pr 3(rм - rв)g; (8.11)
Fс = 6prhм υв , (8.12)
Fц = 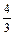 pr 3(rм - rв) υ
pr 3(rм - rв) υ 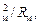 (8.13)
(8.13)
где rм и rв - плотности металла и включения соответственно; υв и υм - скорости движения включения и конвективных потоков металла. Величина DR определяется уравнением [52]:
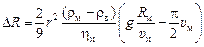 . (8.14)
. (8.14)
Решение. Из рис. 1 видно, что радиус закругления циркуляционных потоков металла в индукционной печи D/2 » 0,45 м. Для того чтобы эти потоки затягивали частицы в объем расплава [DR < 0 в формуле (8.14)], должно выполняться неравенство
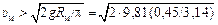 = 1,68 м/с.
= 1,68 м/с.
Таким образом, при скоростях перемешивания более 1,7 м/с включения затягиваются с поверхности в объем ванны металла.
Примечание. Скорость перемешивания металла в индукционных печах значительна (2–5 м/с), поэтому неметаллические включения при выплавке стали в этом агрегате могут затягиваться вглубь и не всегда попадать на границы раздела фаз (металл–шлак, металл–футеровка). При этом, как следует из выражения (8.14), в большей степени затягиваются частицы большего размера (2r) и меньшей плотности (rв).
76. Укрупнение неметаллических включений
в расплавленном металле
Задача. Оценить влияние конвекции на укрупнение включений глинозема в стали при 1873 К.
Исходные данные. 1. Вязкость стали hм = 5×10-3 Па×с, плотность rм = 7,15×103 кг/м3. 2. Градиент скорости конвективных потоков в расплаве металла d υ / dX = 1 с-1. 3. Плотность глинозема rв = 3,97×103 кг/м3.
Теория. Для рафинирования стали от неметаллических включений существенное значение имеет скорость их укрупнения (коагуляции - для твердых и коалесценции - для жидких частиц), которая зависит от частоты встреч частиц в расплаве. Включения сталкиваются в результате теплового хаотичного движения (перикинетическая коагуляция) и различий скоростей движения, вызванных неодинаковыми размерами и плотностями частиц, а также под действием конвективных потоков (ортокинетическая коагуляция).
Скорость перикинетической коагуляции Jп в соответствии с выводами Смолуховского (и для различных сферических включений i и j) равна [53]:
Jп = 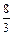 (kT/hм) (ni nj), (8.15)
(kT/hм) (ni nj), (8.15)
где ni и nj - число соответствующих неметаллических частиц в единице объема; k - константа Больцмана.
В рассматриваемом случае изменение концентрации включений п со временем t определяется следующим уравнением [54]:
n = 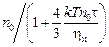 . (8.16)
. (8.16)
Время t, в течение которого число частиц уменьшается вдвое, равно
t = 3hм /(4kTn0). (8.17)
Скорость ортокинетической коагуляции JO , в которой вероятность столкновения в одном направлении больше, чем в остальных, определяется следующим уравнением [54]:
JO = 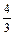 ni nj(Ri j)3(dυ/dX ), (8.18)
ni nj(Ri j)3(dυ/dX ), (8.18)
где R i j = r i + rj - сумма радиусов частиц.
Анализ выражения (8.18) показывает, что различие скоростей всплывания, вызванное неодинаковыми размерами и плотностями неметаллических включений в стали, сравнительно слабо сказывается на частоте встреч, а, следовательно, и на их укрупнении. Существенное увеличение скорости процесса коагуляции обусловлено наличием конвективных потоков в металле с заметным градиентом скорости dυ/dX. Сопоставление скорости укрупнения частиц (вероятности их столкновения) в интенсивно перемешиваемом расплаве по формуле (8.18) и спокойном металле по уравнению (8.15) приводит к следующему выражению:
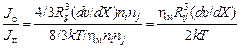 . (8.19)
. (8.19)
Решение. При наблюдаемой на практике концентрации неметаллических включений в стали 0,01 – 0,02 % число частиц глинозема средним размером 2r = 2×10-6 м (2 мкм) в единице объема расплава составляет
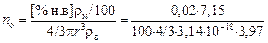 = 1,5×1014 частиц/м3.
= 1,5×1014 частиц/м3.
Время, в течение которого число включений в результате перикинетической коагуляции уменьшится вдвое, согласно уравнению (8.17) равно
t = 3hм /(4kTnо) = (3×5×10-3)/(4×1,38×10-23×1873×1,5×10-14) = 3,86×103 с,
что составляет > 1 ч, т.е. даже для таких малых частиц перикинетическая коагуляция (укрупнение включений в спокойном металле) протекает настолько медленно, что не имеет практического значения. Вибрация металла (механическая или при использовании ультразвука) может заметно ускорить перикинетическую коагуляцию, которая будет охватывать при этом более крупные включения.
Из уравнения (8.19) следует, что при наличии в расплаве конвективных потоков с градиентом скорости dυ/dX = 1 с-1, скорость перикинетической и ортокинетической коагуляции сопоставимы для неметаллических частиц размеров
(ri + rj) = 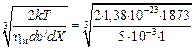 = 2×10-6 м = 2 мкм.
= 2×10-6 м = 2 мкм.
При размере частиц 10-5 м (10 мкм)
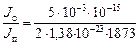 = 102.
= 102.
Если в стали присутствуют более крупные включения размером 10-4 м (100 мкм), то Jо/Jп > 105, поэтому в процессе укрупнения неметаллических включений, ортокинетическая коагуляция под действием конвективных потоков играет определяющую роль. В этой связи перемешивание стали при продувке инертными газами, а также электромагнитное перемешивание способствуют значительному увеличению скорости укрупнения включений.
Примечание. Введение в металл крупных оксидных включений, например, путем эмульгирования шлака при обработке в ковше [как следует из уравнения (8.18)], также благоприятно влияет на скорость укрупнения частиц и эффективность рафинирования стали от неметаллических включений.
77. Движение неметаллических включений
в концентрационном поле
поверхностно-активных примесей
Задача. Рассчитать скорость движения жидкой неметаллической частицы в стали в поле диффузии кислорода (действием гравитационных сил пренебречь).
Исходные данные. 1. Концентрация растворенного кислорода в расплавленном металле 0,015 %. 2. Величина FRT для такого содержания кислорода в стали ~ 300 мДж/м2 (F - адсорбция кислорода на поверхности неметаллической частицы, содержащей до 40 % Аl2O3 ; R - универсальная газовая постоянная; T - абсолютная температура). 3. Среднее значение градиента концентрации кислорода в окрестностях неметаллического включения dc/dx = 0,5×10-1 %/м. 4. Размер включения 2r = 20 мкм = 2×10-5 м. 5. Вязкость расплавленного металла hм = 5×10-3 Па×с.
Теория. Локальные области, характеризующиеся градиентом концентрации поверхностно-активных примесей (кислорода, серы и др.), появляются в результате введения в расплав раскислителей, легирующих добавок, у границ раздела фаз и т.д. Присутствие неоднородных концентрационных полей (полей диффузии) приводит к неравномерной адсорбции вдоль поверхности неметаллической частицы. Возникающий при этом градиент поверхностного натяжения grad s обусловливает возникновение силы, вызывающей механическое перемещение включения в направлении возрастания концентрации поверхностно-активного компонента [55].
Выражение для рассматриваемой силы F имеет вид [3]:
F = -F grad s, (8.20)
где F - полная поверхность частицы.
В соответствии с уравнением Гиббса для двухкомпонентного раствора
G grad m = -grad s. (8.21)
В свою очередь
grad m = (d m/dc)×(dc/dx) = (RT/c)×(dc/dx), (8.22)
где с - концентрация поверхностно-активного компонента.
Подставляя выражения (8.21) и (8.22) в уравнение (8.20), окончательно получаем
F = F(GRT/c)(dc/dx). (8.23)
Выражение для скорости движения включения υ получаем, приравнивая силу F по уравнению (8.23) и силу сопротивления движению в вязкой среде, определяемую формулой
υ = 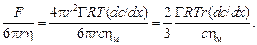 (8.24)
(8.24)
Решение. Подставляя значения соответствующих величин в уравнение (8.24), получаем значение скорости движения частиц размером 20 мкм в поле диффузии кислорода
υ = 2/3[(10-5×300×10-3×0,5×10-1)/(1,5×10-2×5×10-3)] » 1,4×10-3 м/с.
Для сравнения укажем, что скорость всплывания неметаллического включения такого же размера в гравитационном поле под действием выталкивающей силы (см. задачу 73) существенно меньше (1,6×10-4 м/с). Таким образом, миграция включений под действием поверхностных сил может играть заметную роль в процессах укрупнения частиц в локальных объемах расплава и перехода их в шлаковую фазу, а также влиять на распределение включений в слитке
(у фронта кристаллизации наблюдается градиент концентрации поверхностно-активных примесей).
Примечание. Проведен упрощенный расчет скорости движения включения в диффузионном поле без учета того факта, что при перемещении частицы атомы поверхностно-активного вещества сносятся к ее корме, вызывая эффект «адсорбционного торможения».
78. Рафинирование стали от неметаллических включений при капельном переносе в слое расплавленного шлака
Задача. Рассчитать, как изменится содержание неметаллических включений в стали при прохождении капли жидкого металла через слой расплавленного шлака в процессе ЭШП.
Исходные данные. 1. Радиус капли стали, отрывающейся от электрода, r = 0,4 см. 2. Толщина слоя шлака (межэлектродный промежуток)
h = 10 см. 3. Средний размер неметаллических включений d = 10-3 см.
Теория. Электрошлаковый переплав является одним из самых эффективных способов рафинирования стали от неметаллических включений (степень рафинирования достигает 65–75 %). Удаление неметаллических частиц в этом процессе происходит при переходе их в шлаковую фазу из пленки жидкого металла на торце электрода, из падающей капли металла и из жидкой металлической ванны путем всплывания и выноса с конвективными потоками.
Проведем приближенный расчет степени рафинирования стали при капельном переносе в шлаковой фазе. Примем, что толщина рафинируемого слоя металла равна d, т.е. размеру удаляемых включений. Тогда, если капля стали радиусом r проходит в шлаке путь dh, то металл проконтактирует со шлаком по поверхности 2prdh и частицы, находящиеся в этом поверхностном слое, перейдут в шлак. Объем металла, очищенного от включений размером d, составит 2pr d dh, а их количество, перешедшее в шлак, dn = 2pr d cdh. При этом концентрация включений в капле стали с уменьшится на величину
dc = dn/V. Отсюда
-Vdc = 2pr d cdh, (8.25)
где V - объем капли, равный 4/3pr3.
Интегрируя выражение (8.25) в пределах от c0 до с и от h = 0 до h, получаем
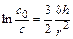 , (8.26)
, (8.26)
где c0 - начальная концентрация включений.
Поправочный коэффициент, учитывающий движение металла на поверхности падающей капли и неправильную форму удаляемых неметаллических частиц, по данным В.В. Хлынова, О.А. Есина и др., равен ~ 2,3. Тогда окончательно расчетное уравнение имеет вид
lg(с0/с) » 1,5(dh/r 2). (8.27)
Решение. Степень рафинирования стали от неметаллических включений размером 10-3 см (10 мкм) при прохождении капли радиусом 0,4 см через слой расплавленного шлака толщиной 10 см по формуле (8.27) равна
lg(с0/с) = 1,5(10-3×10/16×10-2) = 0,09; с0/с = 1,23.
Таким образом, концентрация включений в металле снизится в 1,23 раза, а степень рафинирования [(с0 - с)/с0] 100 % при этом составит
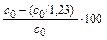 = 19 %.
= 19 %.
Невысокая степень рафинирования объясняется тем, что продолжительность пребывания падающей капли в контакте со шлаком в процессе ЭШП мала и не превышает долей секунды.
Примечание. Основной вклад в рафинирование стали от неметаллических включений при ЭШП вносят процессы удаления частиц из пленки жидкого металла на торце электрода и всплывания их из металлической ванны. Роль капельного переноса возрастает при уменьшении размеров металлических капель, отрывающихся от электрода, и увеличении межэлектродного промежутка (слоя расплавленного шлака).
79. Гомогенное и гетерогенное выделение неметаллических включений в стали
Задача. Оценить возможность выделения нитридных включений непосредственно в объеме жидкого расплава Fe + 0,5 % Ti и на готовых подложках-оксидах при 1873 К.
Исходные данные. 1. Плотности нитрида титана rTiN = 5,4×103 кг/м3; оксида титана rTi2O3 = 4,6×103 кг/м. 2. Поверхностные натяжения расплава sм = 1780 мДж/м2, твердого нитрида титана sв = 2660 мДж/м2. 3. Краевой угол смачивания расплавом нитрида титана q = 100°. 4. Межфазное натяжение на границе оксид титана–расплав sм-в = 1200 мДж/м2.
Теория. Вероятность образования зародышей неметаллических включений в жидкой стали можно оценить, пользуясь известными уравнениями теории зарождения новой фазы [56]:
J = Hexp(-DG*/kT ), (8.28)
где J - число зародышей, возникающих в единице объема расплава за единицу времени; Н - частотный предэкспоненциальный фактор, (см3×с)-1; k - постоянная Больцмана; DG* - изменение энергии Гиббса при образовании сферического зародыша критического размера
DG * = 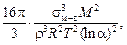 (8.29)
(8.29)
здесь М и r - молекулярная масса и плотность вещества зародыша (неметаллического включения); 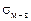 – межфазное натяжение на границе металл–включение; a - степень химического пересыщения расплава реагентами, необходимая для образования включения Rn Х m и равная
– межфазное натяжение на границе металл–включение; a - степень химического пересыщения расплава реагентами, необходимая для образования включения Rn Х m и равная
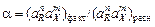 ,
,
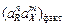 и
и 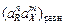 - произведения фактических и равновесных активностей компонентов.
- произведения фактических и равновесных активностей компонентов.
Критическое пересыщение, необходимое для гомогенного выделения включения, можно рассчитать из уравнений (8.28) и (8.29) при J = 1 см-3×с-1, тогда
ln a = 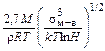 . (8.30)
. (8.30)
Выражение (8.30) позволяет оценить возможность гомогенного выделения неметаллических включений в объеме жидкой стали по величине a. Гетерогенное зародышеобразование (на готовых подложках) требует, как правило, меньших энергетических затрат. Поскольку изменение энергии Гиббса при образовании частицы можно выразить через степень пересыщения
DG * = -RT lna, (8.31)
следовательно
lnaгом /lnaгет = 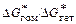 . (8.32)
. (8.32)
Формула (8.32) позволяет сравнить значения степеней пересыщений, необходимых для гомогенного и гетерогенного образования включений в расплаве.
Решение. Для оценки возможности гомогенного выделения нитридных частиц в расплаве Fe–0,5 % Ti рассчитаем по уравнению (8.30) необходимую степень пересыщения расплава титаном и азотом. Величину sм-в определим по формуле Неймана (см. задачу 38)
sм-в = sв - sмcosq = 2660 - 1780×cos 100° = 2980 мДж/м2.
Значение H для различных включений находится в пределах
1026–1029 см-3×с-1 [56, 57]. Примем для данного случая H = 1027 см-3×с-1 =
= 1033 м-3×с-1. Тогда
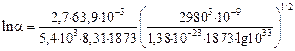 = 11,5; a = 105.
= 11,5; a = 105.
Таким образом, для гомогенного выделения твердых частиц TiN (температура плавления 3103 К) требуется очень большая степень пересыщения расплава азотом и титаном. Такое пересыщение с учетом (aTiaN)равн = 2,9×10-3 возможно при концентрации азота в расплаве
[N]факт = 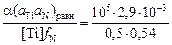 > 100 %,
> 100 %,
что не может быть достигнуто, поэтому гомогенное выделение включений TiN в жидком железе маловероятно.
Необходимую степень пересыщения при образовании твердого при 1873 К оксида титана Ti2О3 можно определить по уравнению (8.30)
ln a = 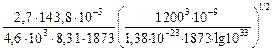 = 7,6; a = 1,9×103.
= 7,6; a = 1,9×103.
С учетом 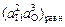 = 2,7×10-9 при 1873 К [57] получаем, что этому пересыщению соответствует концентрация кислорода
= 2,7×10-9 при 1873 К [57] получаем, что этому пересыщению соответствует концентрация кислорода
[O]факт = 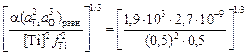 = 3,4×10-2 %.
= 3,4×10-2 %.
Такое содержание [О] является вполне реальным для сталеплавильной ванны.
Оценим теперь возможность гетерогенного образования нитридов титана на оксидных включениях как на готовых подложках. Сравнивая уравнения (8.30) и (8.31), получаем, что DG * ~ 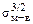 , т.е. примерно пропорционально поверхностной энергии в степени 3/2 [56, 58]. Очевидно, что для выделения зародыша нитрида на оксидном включении поверхностная энергия примерно в 4 раза меньше, чем при гомогенном образовании (~ pr 2sм-в - в первом случае и
, т.е. примерно пропорционально поверхностной энергии в степени 3/2 [56, 58]. Очевидно, что для выделения зародыша нитрида на оксидном включении поверхностная энергия примерно в 4 раза меньше, чем при гомогенном образовании (~ pr 2sм-в - в первом случае и
~ 4pr 2sм-в - во втором, r - радиус зародыша). Тогда
lnaгом /lnaгет = 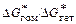 » (4)3/2 = 8.
» (4)3/2 = 8.
Отсюда aгет = (aгом )1/8 » 4 и [N]факт = (4×2,9×10-3)/(0,5×0,54) » 4×10-2 %.
Таким образом, гетерогенное выделение нитридных включений с титаном на готовых подложках-оксидах вполне вероятно, что подтверждается экспериментально [58].
Примечание. Если жидкое включение выделяется на твердой подложке (или твердое - на жидкой частице), то [57]
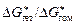 = (2 - 2cosq - sin2q×cosq)/4,
= (2 - 2cosq - sin2q×cosq)/4,
где q - краевой угол смачивания расплавом твердой подложки. В системах твердое включение–шлаковый расплав q мал и, как правило, не превышает 20°, поэтому 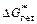 <<
<< 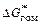 . В промышленной практике гетерогенное зарождение включений играет большую роль, поскольку используемые раскислители и ферросплавы обычно содержат в качестве примесей неметаллические включения - готовые подложки для образования продуктов раскисления и нитридных частиц.
. В промышленной практике гетерогенное зарождение включений играет большую роль, поскольку используемые раскислители и ферросплавы обычно содержат в качестве примесей неметаллические включения - готовые подложки для образования продуктов раскисления и нитридных частиц.
80. Температура начала
образования неметаллических включений
в двухфазной области
Задача. Определить, при какой температуре в двухфазной области начнет выделяться сульфид марганца при затвердевании стали ШХ15CГ.
Исходные данные. 1. Состав жидкой стали: 1,0 % С; 1,0 % Мn; 0,5 % Si; 1,5 % Cr; 0,02 % S; 0,05 % Al; 0,01 % N. 2. Температура ликвидуса Tлик = 1733 К, температура солидуса Tсол = 1613 К. 3. Равновесные коэффициенты распределения углерода 0,25; серы 0,10; азота 0,25; алюминия 0,50; хрома 0,75; марганца 0,74; кремния 0,64. 4. Для реакции [Мn] + [S] = MnS(т) lgK = (11700/7) + 6,790. 5. Температура плавления MnS 1803 K.
Теория. По мере затвердевания металла в двухфазной области маточный раствор обогащается примесями. В объемах, ограниченных осями второго порядка, коэффициенты распределения примесей между твердой и жидкой фазами (K ) практически равны равновесным значениям этих коэффициентов K » K0 . В этих условиях массовая доля примеси в маточном растворе по мере кристаллизации изменяется следующим образом:
сж = с0/(1 - g)l – K0, (8.33)
где с0 - массовая доля примеси в исходном жидком расплаве; g - доля твердой фазы при данной температуре; K0 - равновесный коэффициент распределения примеси. В бинарных системах, если линии ликвидуса и солидуса условно принять за прямые, величину g при температуре Т можно оценить по формуле
g » (Tлик - Т)/(Tлик - Тсол), (8.34)
где Tлик , Тсол - температуры ликвидуса и солидуса. Отсюда
сж = с0[(Tлик - Тсол)(T - Тсол)l – K0]. (8.35)
В формулы для термодинамических расчетов, связанных с процессами в двухфазной области, следует подставлять величины сж , определяемые по выражению (8.35).
Пусть в двухфазной области образуется соединение по реакции
m[Ме] + n[Х ] = Меm Xn.
Константа равновесия в данном случае имеет вид
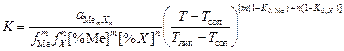 , (8.36)
, (8.36)
где K0, Ме и K0, X - соответственно равновесные коэффициенты распределения элементов Me и X.
При этом надо учесть, что коэффициенты активности fМе и fX зависят от изменения массовых долей компонентов сплава в двухфазной области
lgfi = 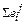 [% j]0[(Tлик - Тсол)(T - Тсол)]l – K0, j . (8.37)
[% j]0[(Tлик - Тсол)(T - Тсол)]l – K0, j . (8.37)
Для решения уравнения для K относительно температуры его удобнее представить в логарифмическом виде:
lg(T - Тсол) = lg(Tлик - Тсол)] +
+ 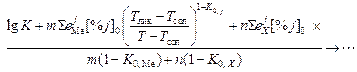
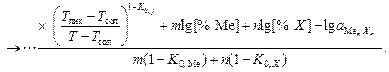
Решение данного уравнения проводится либо на ЭВМ, либо методом подбора.
Решение. При температурах двухфазной области сульфид MnS твердый, и данные о lgK не требуют корректировки. Значения параметров взаимодействия примем на основании данных работы [3]. Если их зависимость от температуры неизвестна, примем
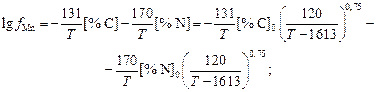
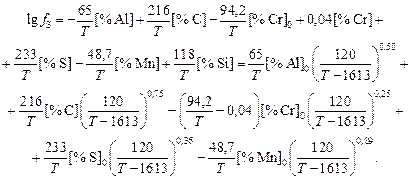
С учетом принятого состава стали имеем
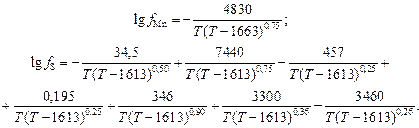
С учетом значений lgK и m = п = 1 K0, Mn = 0,74; K0, S = 0,10 и, считая aMnS = 1, получаем
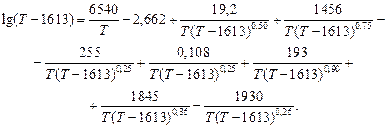
Решая данное уравнение методом подбора, получаем Т = 1653 К.
81. Диссоциация неметаллических
включений в жидкой стали
Задача. Определить продолжительность растворения включений TiN в жидкой стали 08Х18Н10 при 1873 К, приняв, что скорость растворения лимитируется массопереносом титана и азота в расплаве.
Исходные данные. 1. Плотность жидкой стали rм = 7×103 кг/м3. 2. Плотность нитрида rн = 5,2×103 кг/м3. 3. Коэффициенты диффузии титана и азота в стали D Ti = 8×10-9 м2/с и DN = 2×10-8 м2/с. 4. Исходные концентрации азота и титана в стали [N]0 = 0,020 %; [Ti]0 = = 0,10 % (титан вводят для микролегирования).
Теория. Включения TiN растворяются лишь в том случае, если концентрации азота и титана в расплаве меньше соответствующих равновесных с нитридом значений
TiN(т) = [N] + [Ti]. (8.38)
Поскольку скорость растворения лимитируется внутренним массопереносом компонентов, то на границе раздела включение–жидкий металл имеет место равновесие реакции (8.38). Соответствующие концентрации [N]пов и [Ti]пов можно вычислить по значению константы равновесия K1 = [N][Ti] fN fTi . Тогда произведение равновесных поверхностных концентраций
KS = [N]пов[Ti]пов = K1 /(fTi fN). (8.39)
Рассмотрим наиболее простой случай чисто молекулярной диффузии азота и титана от сферического включения в объеме расплава [56]. Диффузионное уравнение второго закона Фика для стационарного условия (dc/dr = 0) в сферических координатах имеет вид
(¶2c/¶R2) + (2/R)(¶с/¶R) = 0, (8.40)
где R - расстояние от центра включения, имеющего радиус r, до некоторой точки в расплаве с концентрацией с.
При последовательном интегрировании уравнения (8.40) получим решение в следующей форме:
с = (А/R) + В, (8.41)
где А и В - постоянные интегрирования, которые можно определить из граничных условий: 1) при R ® ¥ с ® c0 , тогда В = c0 ;
2) при R ® r с = спов , А = r (спов - c0), тогда
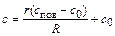 . (8.42)
. (8.42)
Поток вещества от включения равен
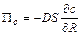 , (8.43)
, (8.43)
где S - площадь поверхности включения.
Отношение ¶с/¶R определим, продифференцировав выражение (8.42):
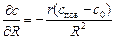 . (8.44)
. (8.44)
Подставляя уравнение (8.44) в выражение (8.43), при R = r и S = = 4pr 2, получаем выражения для потоков азота и титана от поверхности растворяющегося включения
PN = 4pDNr ([N]пов - [N]0); (8.45)
PTi = 4pDTir ([Ti]пов - [Ti]0). (8.46)
За время dt масса включения изменится на dm. Выражая dm через изменение радиуса включения dr, получаем
dm = Srнdr. (8.47)
Выразим dm через поток азота (или титана)
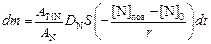 , (8.48)
, (8.48)
где АTiN и AN - молекулярная и атомная массы нитрида и азота. Приравнивая правые части выражений (8.47) и (8.48), получаем
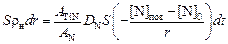 . (8.49)
. (8.49)
Разделяя переменные и интегрируя уравнение (8.49) в пределах: по r от начального радиуса r0 до r и по t от 0 до t, получаем
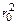 - r 2 = (2ATiN /ANrн)([N]пов - [N]0)t. (8.50)
- r 2 = (2ATiN /ANrн)([N]пов - [N]0)t. (8.50)
Продолжительность полного растворения нитрида соответствует
r = 0, тогда из формулы (8.50) следует, что
t = ( 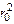 ANrн)/[2ATiNDN([N]пов - [N]0)]. (8.51)
ANrн)/[2ATiNDN([N]пов - [N]0)]. (8.51)
В более общей форме выражение (8.51) имеет вид
t = ( 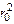 υN)/[2DN([N]пов - [N]0)],
υN)/[2DN([N]пов - [N]0)],
где υN = ANrн/ATiN .
В выражении (8.51) неизвестно значение [N]пов . Принимая во внимание стехиометрию растворяющегося нитрида TiN, запишем (PN /PTi) = АN /АTi, тогда с учетом выражений (8.45) и (8.46) получим
([N]пов - [N]0)/([Ti]пов - [Ti]0) = (AND Ti)/(ATiD N). (8.52)
Решая систему уравнений (8.39) и (8.52), определяем значения [N]пов и [Ti]пов :
[N]пов = 0,5([N]0 - Q [Ti]0) ± 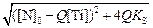 ; (8.53)
; (8.53)
[Ti]пoв = KS /[N]пов , (8.54)
гдe Q = (AND Ti)/(ATiD N).
Решение. Выразим концентрации [N]0 и [Ti]0 в кг/м3, тогда получим [Ti]0 = 7,0 кг/м3 и [N]0 = 1,4 кг/м3. При 1873 К произведение равновесных концентраций [N][Ti] для стали 08Х18Н10 в соответствии с формулой (8.39) - величина постоянная, равная KS = 0,0066 (%)2. Значение KS равно 0,0066×(7×103/100)2 = 32,3 (кг/м3)2.
Вычислим значения [N]пов и [Ti]пов по формулам (8.53) и (8.54), предварительно определив Q:
Q = (14×8×10-9)/(48×2×10-8) = 0,117;
[N]пов = 0,5×(1,4 – 0,117×7,0 ± 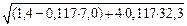 = 2,26 кг/м3;
= 2,26 кг/м3;
[Ti]пов = 32,3/2,26 = 14,3 кг/м3.
По формуле (8.51) определим продолжительность растворения нитридов размерами 1, 10 и 50 мкм.
Для размера 1 мкм
t = [(0,5×10-6)2×14×5,2×103]/[2×62×2×10-8(2,26 - 1,4)] = 0,0085 » 0,01 с.
Продолжительность растворения нитридных включений размером 10 и 50 мкм составляет 0,9 и 21,0 с.
Таким образом, включение нитрида титана размером до 50 мкм в рассмотренных условиях полностью диссоциирует, если продолжительность пребывания его в расплаве превысит 21 с.
Примечание. В условиях движущейся жидкости на растворение включений влияют характеристики потоков в расплаве. В металлической ванне размер потоков обычно во много раз больше размера включений, поэтому включения движутся вместе с потоками металла и относительно потока перемещаются с небольшими скоростями, в основном в результате всплывания. При небольших размерах включений учесть скорость всплывания можно при помощи интерполяционного выражения для потока вещества (азота или титана) от включения [59]
PN = 4pDNr (1 + 0,64Pе1/3)([N]пов - [N]0), (8.55)
где Pe - критерий Пекле, характеризующий отношение потоков, обусловленных переносом движущейся жидкостью и диффузией,
Ре = υ r/DN. Будем считать, что скорость всплывания частицы описывается уравнением Стокса [3]:
υ = 2/9gr 2[(rм - rн)h], (8.56)
где g - ускорение свободного падения; h - динамическая вязкость стали.
Подставим выражение (8.56) в формулу для Ре, а затем полученное выражение в уравнение (8.55). После преобразований, аналогичных (8.47) – (8.49), получим выражение для продолжительности полного растворения нитрида, учитывающее скорость его всплывания:
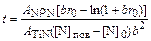 , (8.57)
, (8.57)
где
b = 0,64 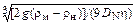 . (8.58)
. (8.58)
Для жидкой стали h = 0,006 Па×с. Тогда
b = 0,64 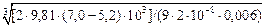 = 20460.
= 20460.
Для нитридов размером 50 мкм
t = 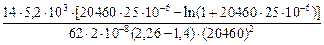 = 16 c.
= 16 c.
Это несколько меньше продолжительности растворения неподвижного включения (21 с). Для включений малого размера (1 и 10 мкм) учет скорости всплывания дает практически те же значения продолжительности растворения (0,01 и 0,9 с соответственно).
9. Внепечная обработка
82. Обезуглероживание
хромсодержащего расплава
при продувке аргоно-кислородной смесью
Задача. Рассчитать изменение концентраций углерода, хрома и температуры металла в процессе продувки высокохромистого расплава аргоно-кислородной смесью.
Исходные данные. 1. Состав полупродукта: 1,16 % С; 17,29 % Сr; 10 % Ni; 0,4 % Si. 2. Экспериментальные данные по продувке в 45-т конвертере [60] приведены ниже:
| Н.п. | t, мин | qAr , м3/(т×мин) | qO2 , м3/(т×мин) | [C]к , % | [Cr]к , % | T, К |
| - | - | - | 1,16 | 17,29 | 1748 | |
| I | 23 | 0,18 | 0,52 | 0,41 | 16,9 | 1923 |
| II | 10 | 0,25 | 0,50 | 0,12 | 16,7 | 1998 |
| III | 6,5 | 0,51 | 0,26 | 0,047 | 16,45 | 2003 |
| Примечание. Н.п. - начало продувки, I, II, III - моменты окончания периодов продувки; qAr , qO2 - расход газов, [С]к , [Сr]к - состав металла в конце периода, t - продолжительность периода. | ||||||
3. Теплоемкость металла СMe = 0,838 кДж/(кг×К). 4. Средняя теплоемкость аргона и кислорода СAr = 0,928 кДж/(м3×К), СO2 =
= 1,545 кДж/(м3×К); начальная температура их смеси Tг = 298 К. 5. Удельные тепловые эффекты реакций [8, 61]:
[С] +  1/2O2 (г) = СО(г); НC = 11100 кДж/кг;
1/2O2 (г) = СО(г); НC = 11100 кДж/кг;
3[Cr] + 2O2 (г) = Сr3O4 (т); НCr = 9570 кДж/кг;
[Si] + О2 (г) = SiO2 (т); НSi = 25400 кДж/кг;
Fe(ж) +  O2 (г) = FeO(ж); НFe = 4000 кДж/кг.
O2 (г) = FeO(ж); НFe = 4000 кДж/кг.
Теория. Продувка коррозионностойкой стали аргоно-кислородной смесью позволяет окислить углерод по реакции (9.1) без заметных потерь хрома
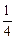 Сr3O4 (т) + [С] =
Сr3O4 (т) + [С] = 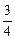 [Сr] + СО(г) ; (9.1)
[Сr] + СО(г) ; (9.1)
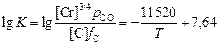 . (9.2)
. (9.2)
При кислородной продувке в открытой печи давление СО близко к 1 атм. При продувке расплава смесью кислорода с газом-разбавителем pCO < 1 атм. Понижение pCO обеспечивает смещение равновесия реакции (9.1) вправо, т.е. способствует получению низких концентраций углерода и уменьшению угара хрома.








