Исходные данные. Те же, что в задаче 59. Статическим давлением столба металла и шлака, а также давлением в пузыре, обусловленным поверхностными силами, пренебрегаем.
Теория. Термодинамические причины и пределы протекания процессов, рассмотренные в задачах 58 и 59, справедливы независимо от механизма переноса компонентов в объеме шлака (диффузия, конвективный перенос и др.). Одним из наиболее эффективных режимов дегазации является пузырьковый режим (химическое кипение), возникающий, когда сумма равновесных парциальных давлений растворенных газов превышает внешнее давление: 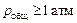 (101325 Па).
(101325 Па).
Общее давление газа в пузыре, с учетом принятых допущений в исходных условиях, равно сумме парциальных давлений водяного пара, кислорода и водорода:
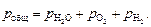 (6.38)
(6.38)
Однако в глубоко раскисленном шлаке парциальные давления водяного пара и кислорода составляют очень малые величины, и в качестве условия образования пузырей можно принять
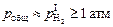 (101325 Па). (6.39)
(101325 Па). (6.39)
Индекс I относится к верхней границе шлака, индекс II – к нижней. Рассмотрим конвективный перенос элементарного объема шлака от границы раздела II (рисунок), где шлак находится в равновесии с металлом.
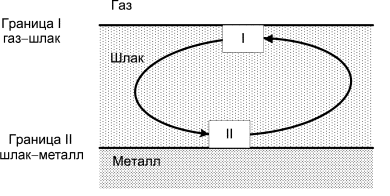
Схема конвективного переноса элементарных порций шлака
Если элементарный объем шлака на границе II находится в равновесии с металлом, то между растворенным в нем водородом и равновесными парциальными давлениями водорода и кислорода выполняется зависимость [3]
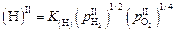 . (6.40)
. (6.40)
При конвективном перемещении этого объем шлака к поверхности раздела I (газ–шлак) содержание в нем растворенного водорода останется неизменным:
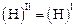 . (6.41)
. (6.41)
Но в результате контакта с восстановительной атмосферой (как показал результат расчета задачи 59) уменьшится окисленность шлака и он окажется пересыщенным по водороду, т.е. в нем возрастает давление водорода в соответствии с формулой
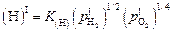 . (6.42)
. (6.42)
Из выражений (6.40) – (6.42) следует, что
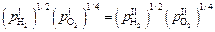 ,
,
откуда
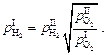 (6.43)
(6.43)
Условие образования пузырей водорода, согласно уравнениям (6.39) и (6.43), можно записать в виде
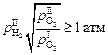 (101325 Па). (6.44)
(101325 Па). (6.44)
Величины 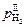 и
и 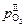 определяются заданными содержаниями водорода и кислорода (с использованием закона Сивертса), поэтому, согласно выражению (6.44), для обеспечения режима химического кипения необходимо поддерживать окисленность границы газ–шлак
определяются заданными содержаниями водорода и кислорода (с использованием закона Сивертса), поэтому, согласно выражению (6.44), для обеспечения режима химического кипения необходимо поддерживать окисленность границы газ–шлак 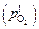 на уровне
на уровне
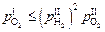 . (6.45)
. (6.45)
Решение. Определим величину равновесного парциального давления водорода на границе шлак–металл (см. задачи 58 и 59):
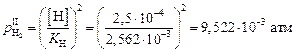 ,
,
то же для 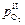 :
:
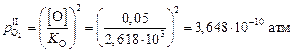 .
.
Необходимая степень раскисления поверхностного слоя шлака составляет
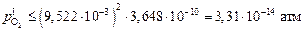 .
.
Таким образом, для реализации удаления водорода из жидкого железа в пузырьковом режиме до уровня 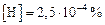 необходимо на границе газ–шлак поддерживать
необходимо на границе газ–шлак поддерживать 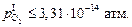 При этом при переплаве более окисленного металла требуется менее глубокое раскисление поверхности шлак–газ.
При этом при переплаве более окисленного металла требуется менее глубокое раскисление поверхности шлак–газ.
Примечание. Найденная степень раскисления может быть достигнута при использовании таких раскислителей, как кальций, магний, алюминий, углерод, а также газовых смесей с низким содержанием кислорода. В последнем случае, однако, следует иметь в виду, что одновременно с водородом в газовую фазу переносится и кислород (в рассмотренном примере шлак «раскисляется» от уровня 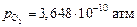 до
до 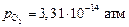 ). При этом с каждым молем водорода в газовую фазу поступает 0,5 моля кислорода, в результате чего резко возрастает
). При этом с каждым молем водорода в газовую фазу поступает 0,5 моля кислорода, в результате чего резко возрастает 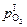 . По этой причине использование газового раскисления на практике может быть малоэффективным.
. По этой причине использование газового раскисления на практике может быть малоэффективным.
61. Термодинамические условия образования неметаллических включений в стали
Задача. На примере нитрида титана вывести общее уравнение, определяющее термодинамические условия его существования в стали. Определить, при какой концентрации азота в стали 08Х18Н10Т при 1923 К образуются нитриды титана.
Исходные данные. 1. Ti(т) +  N2 (г) = TiN(т);
N2 (г) = TiN(т); 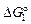 = -334500 +
= -334500 +
+ 93,0Т Дж/моль. 2. Температура и энтальпия плавления титана соответственно равны: Тпл = 1940 К; DHпл = 15500 Дж/моль. 3. Ti(ж) = [Ti](1 % в Fe); 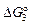 = -69500 - 27,28Т Дж/моль. 4.
= -69500 - 27,28Т Дж/моль. 4.  N2 (г) = [N](1 % в Fe);
N2 (г) = [N](1 % в Fe); 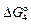 = 10500 +
= 10500 +
+ 20,37Т Дж/моль. 5. Химический состав стали 08Х18Н10Т: 0,08 % С; 18 % Сr; 10 % Ni; 0,6 % Ti.
Теория. Число степеней свободы в соответствии с правилом фаз Гиббса
c = k - Ф + 2. (6.46)
В обсуждаемой системе общее число переменных равно трем ([N], Т и [Ti]). Максимальное число фаз (Ф) также равно трем: расплав на основе железа, газообразный азот и нитрид титана. Число компонентов k определяется как разность между числом химически индивидуальных веществ (железо, титан, нитрид титана) и числом уравнений, их связывающих, поэтому k = 3. Легирующие компоненты (хром, никель) при расчете k не учитывались, так как концентрации их постоянны и в химических реакциях они не участвуют. Другими словами, основа сплава считается одним компонентом. Тогда с = 3 - 3 + + 2 = 2. Таким образом, достаточно задать две переменные из трех для того, чтобы определить состояние данной системы. Выберем в качестве независимых переменных Т и [Ti]. Тогда третий параметр [N] можно определить из уравнения, связывающего три указанных параметра. Таким уравнением является выражение константы равновесия реакции образования нитрида титана:
[Ti] + [N] = TiN(т), 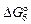 ; (6.47)
; (6.47)
K6 = l/([% Ti]fTi [% N]fN). (6.48)
Прологарифмировав выражение (6.48) и учтя, что lg K6 =
= 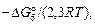 получим
получим
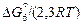 = lg[% Ti] + lg fTi + lg[% N] + lg fN × (6.49)
= lg[% Ti] + lg fTi + lg[% N] + lg fN × (6.49)
Значение 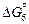 можно получить алгебраическим сложением следующих уравнений:
можно получить алгебраическим сложением следующих уравнений:
Ti(т) +  N2 (г) = TiN(т),
N2 (г) = TiN(т), 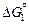 ;
;
Ti(т) = Ti(ж), 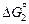 ;
;
Ti(ж) = Ti(1 % в Fe), 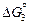 ;
;
 N2 (г) = [% N](1 % в Fe),
N2 (г) = [% N](1 % в Fe), 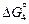
[Ti](1 % в Fe) + [N](1 % в Fe) = TiN(тв); 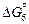 =
= 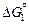 -
- 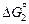 -
- 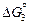 -
- 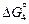 .
.
Выражение температурной зависимости энергии Гиббса плавления титана 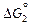 = =
= = 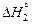 -
- 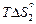 = DHпл - TDSпл получим из условия, что
= DHпл - TDSпл получим из условия, что 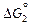 = 0 при Т = Тпл . Тогда DSпл = DHпл /Tпл и
= 0 при Т = Тпл . Тогда DSпл = DHпл /Tпл и 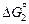 =15500 –
=15500 – 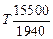 = 15500 -
= 15500 -
– 8,0Т Дж/моль. Соответственно 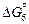 = -291000 + 107,91T Дж/моль. Зависимость fTi от Т можно установить с использованием ТКР[3]:
= -291000 + 107,91T Дж/моль. Зависимость fTi от Т можно установить с использованием ТКР[3]:
lgfTi = 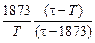 lgfTi(1873) ,
lgfTi(1873) ,
где t - параметр теории, t = 7000 К.
Тогда
lgfTi = 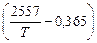 lgfTi (1873). (6.50)
lgfTi (1873). (6.50)
Температурную зависимость fN рассчитаем по уравнению Чипмана и Корригана:
lgfN = 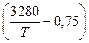 lgfN(1873). (6.51)
lgfN(1873). (6.51)
После подстановки значения 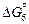 и уравнений (6.50) и (6.51) в выражение (6.49) получим общее уравнение, связывающее три переменные (T, [N], [Ti]) и определяющее термодинамические условия существования нитридов титана:
и уравнений (6.50) и (6.51) в выражение (6.49) получим общее уравнение, связывающее три переменные (T, [N], [Ti]) и определяющее термодинамические условия существования нитридов титана:
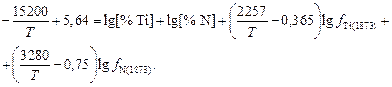 (6.52)
(6.52)
Решение. Для того чтобы определить [% N] по уравнению (6.52), вначале следует вычислить fN и fTi при 1873 К (см. задачу 16);
lg fN (1873) = -0,95.
В выражение
lgfTi(1873) = 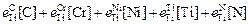
входит неизвестная величина [% N], поэтому расчет [% N] проводится методом итераций. Примем, что начальное значение [N]O = 0. Тогда lg fTi (1873) = 0,4 и из выражения (6.52) можно вычислить следующее значение концентрации азота [N]1, соответствующее lg fTi (1873) = 0,4:
lg[N]1 = 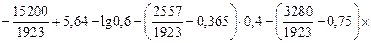
´ (-0,95) = -1,52; [% N]1 = 0,030.
Теперь можем уточнить значение lgfTi. Учитывая, что [N] = 0,030 %, lgfTi (1873) = 0,4 - 1,8×0,030 = 0,346.
По формуле (6.52) вновь вычислим значение [N] = [N]2 , соответствующее более точному lgfTi = 0,346. Получим [N]2 = 0,034 %. Уточняем fTi(lgfTi (1873) = 0,4 - 1,8×0,034 = 0,34) и соответственно получаем [N]3 = = 0,0345 %. Аналогично [N]4 = 0,0347 %. Различие между [N]3 и [N]4 очень мало, и за окончательный результат принимаем [N] » 0,035 %. Таким образом, при 1923 К в стали 08Х18Н10Т, содержащей 0,6 % Ti, нитриды титана образуются при концентрации [N] > 0,035 %.
Примечание. Для вычисления рN2 , соответствующего образованию нитрида титана, можно воспользоваться данными о растворении азота в железе (см. исходные данные, пункт 4). При растворении азота в стали значение константы равновесия K4, записанной в виде выражения K4 = [N] 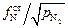 , не изменяется. Тогда рN2 = ([N]
, не изменяется. Тогда рN2 = ([N] 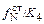 )2. При 1923 К ln K4 =
)2. При 1923 К ln K4 = 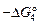 / RT = -(10500 + 20,37×1923)/(8,314×1923) = -3,107; K4 = 0,0447.
/ RT = -(10500 + 20,37×1923)/(8,314×1923) = -3,107; K4 = 0,0447.
lg fN » 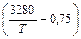 lg fN(1873) =
lg fN(1873) = 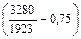 (-0,95) = -0,908;
(-0,95) = -0,908;
fN = 0,124.
Тогда давление азота, соответствующее образованию TiN в стали 08ХН18Н10Т при 1923 К, равно рN2 = (0,035×0,124/0,0447)2 = 0,009 атм.
62. Растворимость газов в легированной стали
Задача. Рассчитать растворимость азота (водорода) в легированной стали при заданных температуре и давлении.
Исходные данные. 1. Состав стали: 18 % Сr; 9 % Ni; 0,5 % Si; 1,5 % Mn. 2. Температура 1923 К. 3. Давление газов: рN2 = 0,25 атм, рH2 = 0,25 атм. 4.  N2 (г) = [N](1 % в Fe); lgKN =
N2 (г) = [N](1 % в Fe); lgKN = 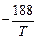 - 1,25 [3]. 5.
- 1,25 [3]. 5.  H2 (г) = [H](1 % в Fe) ; lg KH =
H2 (г) = [H](1 % в Fe) ; lg KH = 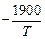 - 1,577 [3].
- 1,577 [3].
Теория. Рассмотрим два расплава: железо и сталь 12Х18Н9, находящиеся в равновесии с газовой фазой (например, азотом) при давлении рN2 и температуре Т. Очевидно, что активность азота, растворенного в железе 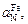 равна активности азота в сплаве
равна активности азота в сплаве 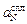 :
: 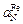 =
= 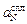 или
или
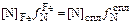 . (6.53)
. (6.53)
Учитывая, что коэффициент активности азота в железе 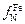 = 1, получаем из выражения (6.53)
= 1, получаем из выражения (6.53)
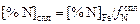 . (6.54)
. (6.54)
Из уравнения константы равновесия процесса растворения азота в железе (см. исходные данные)
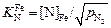 (6.55)
(6.55)
получим [N]Fe и подставим в выражение (6.54). Тогда
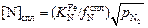 . (6.56)
. (6.56)
Прологарифмируем выражение (6.56):
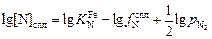 . (6.57)
. (6.57)
Значение 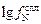 при 1873 К можно вычислить, использовав соответствующие параметры взаимодействия
при 1873 К можно вычислить, использовав соответствующие параметры взаимодействия 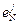 и
и 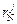 :
:
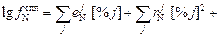 ... (6.58)
... (6.58)
Для пересчета fN и fH на другие температуры часто используют эмпирические уравнения [3]
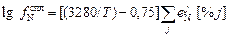 ; (6.59)
; (6.59)
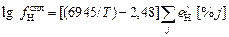 . (6.60)
. (6.60)
Для оценки и анализа результатов расчета можно использовать, в частности, формулы ТРР
lg fN = (1873/T )lgfN (1873) (6.61)
и ТКР
lg fN = 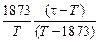 lgfN(1873), (6.62)
lgfN(1873), (6.62)
где t - параметр теории, t = 7000 К.
Строгий расчет растворимости газов в легированной стали требует знания параметров высших порядков, сведения о которых в литературе ограничены. В связи с этим заслуживает внимания формула (6.63), предложенная Л.А. Большовым [32] (см. также [3, с. 63] ) для расчета растворимости азота в сплавах железа и никеля с переходными металлами. Формула хорошо описывает экспериментальные данные при использовании лишь параметров первого порядка:
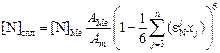 , (6.63)
, (6.63)
где [N]спл и [N]Me - растворимости азота (%) при 1873 К в сплаве и чистом металле-растворителе соответственно; х j - мольная доля j-го компонента в сплаве; 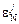 - параметр взаимодействия, описывающий влияние j-го компонента на коэффициент активности азота; п - число компонентов сплава, причем индексы 1 и 2 присваиваются металлу-растворителю Me и азоту соответственно; AMe и А m - массы моля металла-растворителя Me и моля сплава соответственно;
- параметр взаимодействия, описывающий влияние j-го компонента на коэффициент активности азота; п - число компонентов сплава, причем индексы 1 и 2 присваиваются металлу-растворителю Me и азоту соответственно; AMe и А m - массы моля металла-растворителя Me и моля сплава соответственно;
А m = AMexMe + 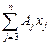 ; (6.64)
; (6.64)
А j - атомная масса j-го компонента.
Роль металла-растворителя Me в уравнении (6.64) может играть как железо, так и никель независимо от их содержания в сплаве, и величины [N]Me, А и 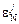 должны соответствовать выбранному растворителю.
должны соответствовать выбранному растворителю.
При расчете растворимости азота в никелевых сплавах в связи с недостатком данных о параметрах взаимодействия в никеле в качестве растворителя можно принять железо. Средняя относительная погрешность расчетного значения растворимости азота при этом составляет около 30 % [33]. Это достаточно близко к погрешности 20 %, получающейся при использовании формулы (6.63), если за растворитель выбрать никель и известные для него параметры взаимодействия [33].
Решение. Вычисления проведем по формуле (6.57), подставив в нее соответственно выражения 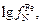
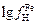 (6.59) и (6.60):
(6.59) и (6.60):
lg[N]спл = 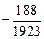 - 1,25 + 0,5 lg 0,25 -
- 1,25 + 0,5 lg 0,25 - 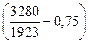 (-0,047×18 +
(-0,047×18 +
+ 0,0063×9 - 0,02×1,5 + 0,047×0,5 + 0,00032×182 + 0,00007×92 -
- 0,00008×18×9) = -0,98; [N]спл = 0,105 %;
lg[H]спл = 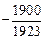 - 1,577 + 0,5 lg 0,25 -
- 1,577 + 0,5 lg 0,25 - 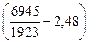 (-0,0022×18 +
(-0,0022×18 +
+ 0×9 - 0,0014×1,5 + 0,027×0,5) = -2,834; [Н]спл = 0,00146 %.
Приведем пример использования формулы (6.63) для расчета растворимости азота в никелевом сплаве (66,4 % Ni + 0 % Fe + 22 % Cr +
+ 11 % W + 0,6 % Al) при 1873 К и рN2 = 1 атм. В качестве растворителя для этого сплава условно примем железо.
В железе при 1873 К параметры взаимодействия следующие [3]:
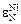 = +2,4;
= +2,4; 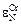 = -10,0;
= -10,0; 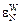 = -3,4;
= -3,4; 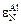 = -2,6.
= -2,6.
Мольные доли компонентов в сплаве такие:
хNi = 0,69; хCr = 0,2595; хW = 0,0368; хAl = 0,0136; xFe = 0.
Вычислим по формуле (6.64) массу моля сплава:
А m = 56×0 + 59×0,69 + 52×0,2595 + 184×0,0368 + 27×0,0136 = 61,34 » 61.
При 1873 К и рN2 = 1 атм растворимость азота в железе равна 0,045 % [33]. Тогда по уравнению (6.63)
[N]спл = 0,045 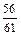 (1 -
(1 - 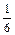 (2,4×0,69 - 10,0×0,2595 - 3,4×0,0368 -
(2,4×0,69 - 10,0×0,2595 - 3,4×0,0368 -
- 2,6×0,0136)6 = 0,113 %.
Экспериментальное значение растворимости [34] 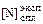 = 0,089 %. Относительная погрешность расчета составляет
= 0,089 %. Относительная погрешность расчета составляет
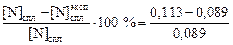 ×100 % » 27 %.
×100 % » 27 %.
Если расчет [N]спл провести [33] по уравнению (6.63), приняв за растворитель никель (ANi » 59; при 1873 К и рN2 = 1 атм [% N]Ni =
= 0,0015 %), то [% N]спл = 0,0015 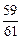 (1 -
(1 - 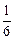 (-4,0×0 - 20,2×0,2595 -
(-4,0×0 - 20,2×0,2595 -
- 18×0,0368 + 0,54×0,0136)6 = 0,088 %, что практически совпадает с экспериментальным значением (0,089 %).
Для сравнения отметим, что при вычислении fN по уравнению (6.58) и использовании параметров только первого порядка [N]спл = = 0,415 %; 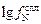 = -0,10×22 - 0,022×11 = -2,442;
= -0,10×22 - 0,022×11 = -2,442; 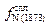 = 0,0036. И по уравнению (6.54) [N] = 0,0015/0,0036 = 0,415 %.
= 0,0036. И по уравнению (6.54) [N] = 0,0015/0,0036 = 0,415 %.
Учитывая 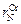 = 0,00103, получаем
= 0,00103, получаем 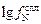 = -0,10×22 - 0,022×11 +
= -0,10×22 - 0,022×11 +
+ 0,00103×222 = -1,943; 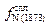 = 0,0114; [N]спл = 0,0015/0,0114 = 0,13 %, т.е. относительная погрешность расчета азота в никелевом сплаве даже при использовании параметра второго порядка остается достаточно высокой (46 %), выше, чем при использовании параметров взаимодействия только первого порядка в формуле (6.63).
= 0,0114; [N]спл = 0,0015/0,0114 = 0,13 %, т.е. относительная погрешность расчета азота в никелевом сплаве даже при использовании параметра второго порядка остается достаточно высокой (46 %), выше, чем при использовании параметров взаимодействия только первого порядка в формуле (6.63).
Таким образом, растворимость азота в высоколегированных сплавах на основе железа и никеля можно рассчитывать, используя формулы (6.58) и (6.63).
63. Погрешности расчетного значения растворимости газов в стали
Задача. Определить погрешность расчетного значения растворимости азота (водорода) в стали заданного состава при 1873 К.
Исходные данные. 1. Химический состав стали Р6М5: 0,85 % С; 4,1 % Сr; 5,2 % Мо; 6,0 % W; 2,0 % V. 2. Для температурной зависимости растворимости азота в жидком железе принять уравнение [38], в котором указана стандартная погрешность коэффициентов:
 N2 (г) = [N]Fe ; lg KFe = [(-824 ± 62)/T ] - 0,910 ± 0,032. (6.65)
N2 (г) = [N]Fe ; lg KFe = [(-824 ± 62)/T ] - 0,910 ± 0,032. (6.65)
3. Параметры взаимодействия 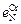 = -0,047;
= -0,047; 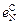 = 0,13;
= 0,13; 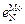 = -0,011;
= -0,011; 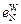 = -0,0015;
= -0,0015; 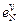 = -0,093.
= -0,093.
Теория. Согласно данным [37] стандартной погрешностью S некоторой величины А называют такую погрешность DА, при которой истинное значение А с вероятностью 67 % находится в интервале Аср ± DA. При этом должно выполняться следующее условие: случайные погрешности подчиняются нормальному распределению, а систематическими можно пренебречь.
Растворимость азота (или водорода) в сплаве данного состава описывается уравнением (см. задачу 62)
[N] = [N]Fe /fN. (6.66)
Стандартную погрешность расчетного значения растворимости азота S можно легко определить, если известна относительная стандартная погрешность (S/[N]), которая для уравнения (6.66) может быть рассчитана по формуле [37]:
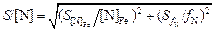 , (6.67)
, (6.67)
где S[N]Fe - стандартная погрешность растворимости азота в чистом растворителе (железе); S fN - стандартная погрешность коэффициента активности азота в стали.
Относительная погрешность растворимости азота в чистом растворителе (S[N]Fe/[N]Fe) равна относительной погрешности константы равновесия процесса растворения азота в железе КFe . Действительно,
KFe = [N]Fe / 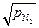 . (6.68)
. (6.68)
Преобразуем и прологарифмируем выражение (6.68):
ln[N]Fe = lnKFe + 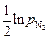 . (6.69)
. (6.69)
Дифференцируем lg[N]Fe , при этом влиянием давления рN2 на погрешность [N]Fe пренебрегаем:
d [N]Fe /[N]Fe = dKFe /KFe . (6.70)
Переходя от дифференциалов к конечным приращениям, получаем
S[N]Fe /[N]Fe = S KFe /KFe , (6.71)
где S KFe - стандартная погрешность KFe .
Легко показать, что
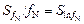 . (6.72)
. (6.72)
Значение fN обычно определяют с помощью параметров взаимодействия 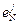 :
:
ln fN = 2,3 lg fN » 2,3 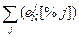 . (6.73)
. (6.73)
Если известны погрешности отдельных параметров 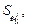 то, используя выражения (6.72) и (6.73) согласно данным [37], можно записать
то, используя выражения (6.72) и (6.73) согласно данным [37], можно записать
(S fN /fN)2 = S2lnfN = 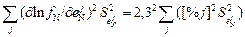 . (6.74)
. (6.74)
Подставив выражения (6.71) и (6.72) в формулу (6.67), получим
S/ [N] = 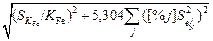 . (6.75)
. (6.75)
При использовании в выражении (6.75) параметров взаимодействия высших порядков 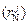 формула (6.75) не изменится, если между ними и параметрами
формула (6.75) не изменится, если между ними и параметрами 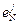 нет корреляции, т.е. если
нет корреляции, т.е. если
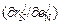 = 0.
= 0.
Данных о погрешностях параметров 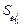 очень мало. Лишь в последние годы при публикации получаемых значений
очень мало. Лишь в последние годы при публикации получаемых значений 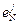 авторы начали указывать их погрешности. В связи с этим значения
авторы начали указывать их погрешности. В связи с этим значения 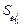 в настоящее время чаще всего оценивают, сравнивая данные, полученные разными авторами, по различным методикам.
в настоящее время чаще всего оценивают, сравнивая данные, полученные разными авторами, по различным методикам.
Решение. Рассчитаем стандартные относительную и абсолютную погрешности расчетного значения растворимости азота в стали Р6М5 при рN2 = 1 атм и 1873 К.
Из выражения (6.65) при 1873 К получим
lg KFe = [(-824 ± 62)/1873] - (0,910 ± 0,032) = -1,350 ± 0,065
или
KFe » 0,045 ± 0,007, т.е. S KFe = 0,007.
Анализ опубликованных данных о параметрах взаимодействия показывает, что их стандартная погрешность обычно не меньше 10 %. Для данного расчета примем ее равной 10 %. Из исходных данных имеем 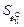 = (0,13×10 %)/100 % = 0,013. Аналогично получим
= (0,13×10 %)/100 % = 0,013. Аналогично получим 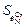 = 0,0047;
= 0,0047; 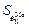 = 0,0011;
= 0,0011; 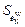 = 0,00015;
= 0,00015; 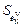 = 0,0093.
= 0,0093.
Вычислим (S/[N]) по формуле (6.75):
S/[N] = 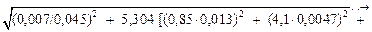
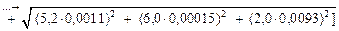 = 0,1698 » 0,17,
= 0,1698 » 0,17,
или ~ 17 %.
Таким образом, относительная стандартная погрешность (S/[N]) расчетного значения растворимости азота в стали Р6М5 при 10 %-ной погрешности параметров взаимодействия составляет 17 %. Основной вклад в эту величину в данном случае вносит погрешность растворимости азота в железе (S[N]Fe/[N]Fe) = 0,007/0,045 = 0,155, или 15,5 %.
При погрешности параметров более 35 % влиянием погрешности растворимости азота в железе (S KFe/ KFe ) в данном случае практически можно пренебречь, так как величина 5,304S([% j] 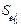 )2 более чем в два раза превышает (S KFe /KFe ) [37]. Даже при очень большой погрешности всех параметров (50 и 100 %) общая погрешность растворимости азота в данной стали (S/[N]) равна соответственно 37 и 70 %, т.е. меньше погрешности самих параметров. Очевидно, этим можно объяснить обычно наблюдаемое удовлетворительное согласование экспериментальных данных по растворимости газов в легированных сталях с результатами расчетов, при выполнении которых используют различные значения параметров взаимодействия.
)2 более чем в два раза превышает (S KFe /KFe ) [37]. Даже при очень большой погрешности всех параметров (50 и 100 %) общая погрешность растворимости азота в данной стали (S/[N]) равна соответственно 37 и 70 %, т.е. меньше погрешности самих параметров. Очевидно, этим можно объяснить обычно наблюдаемое удовлетворительное согласование экспериментальных данных по растворимости газов в легированных сталях с результатами расчетов, при выполнении которых используют различные значения параметров взаимодействия.
Теперь вычислим абсолютную погрешность растворимости азота в стали Р6М5 при 1873 К и рN2 = 1 атм. Из формулы (6.73) lgfN = = 0,13×0,85 - 0,047×4,1 - 0,011×5,2 - 0,0055×6 - 0,093×2 = - 0,344, fN = = 0,463. Согласно формуле (6.66) [N] = 0,045/0,463 = 0,0972 %. Тогда абсолютная стандартная погрешность растворимости азота в стали Р6М5 при 10 %-ной погрешности параметров взаимодействия составляет S = 0,17×0,0972 = 0,0165 » 0,016 % и [N] = (0,097 ± 0,016) %. При 50 %-ной погрешности всех параметров S = 0,37×0,0972 » 0,037 и [N] » (0,100 ± 0,037) %.
64. Условия существования карбонитридов титана в жидкой стали
Задача. Оценить температуры образования нитридов и карбонитридов в стали 15Х25Т.
Исходные данные. Состав стали 15Х25Т: 0,13 % С; 25 % Сr; 0,7 % Ti; 0,08 % N.
Теория. Реакции образования нитридов и карбидов в жидкой стали имеют вид
[Ti] + [N] = (TiN); lg К1 = (15200/T) - 5,6; (6.76)
[Ti] + [С] = (TiC); lg К2 = (8100/T) - 4,8. (6.77)
Известно, что нитриды и карбиды титана образуют непрерывный ряд твердых растворов. Предполагая, что карбонитриды, образующиеся в стали, являются совершенными растворами, т.е. aTiC = xTiC и aTiN = xTiN , можно записать следующую систему уравнений:
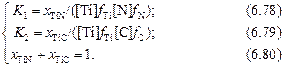
При заданном составе металла решение системы уравнений
(6.78) – (6.80) позволяет определить равновесный с металлом состав карбонитридов и температуру их образования.
Примем, что температурная зависимость fN определяется уравнением Чипмана – Корригана:
lg fN = [(3280/7) - 0,75] lg fN (1873). (6.81)
Зависимость fTi и fC от температуры определяем, используя ТКР (см. задачу 19):
lgfTi = [(2557/T) – 0,365] lg fTi (1873); (6.82)
lgfC = [(2557/T) – 0,365] lg fC (1873) . (6.83)
Значения fN , fTi , fC при 1873 К определяем по параметрам взаимодействия (см. задачу 16).
Логарифмируя уравнения (6.78) и (6.79) и подставляя значения lgK1 и lgК2 , имеем:
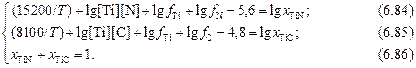
Введя обозначения
А = lg([Ti][N]) + lg fTi + lg fN – 5,6; (6.87)
В = lg ([Ti] [С]) + lg fTi + lg fC – 4,8, (6.88)
получим следующую систему уравнений:
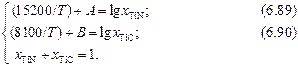
Исключим одно из неизвестных (например, Т ). Для этого умножим уравнение (6.89) на 8100/15200 = 0,533. Вычтя из полученного выражения уравнение (6.90), получим
0,533А - В = 0,533 lg хTiN - lg хTiC . (6.91)
Подставив в уравнение (6.91) выражение хTiN = 1 - хTiC и преобразовав его, получим
хTiC = [ехр(2,3(В - 0,533А))](1 - хTiC)0,533. (6.92)
Уравнение (6.92) является трансцендентным. Величину хTiC можно определить, решив его методом последовательных приближений (итераций).
Зная хTiC (или хTiN = 1 - хTiC), по уравнению (6.89) находим приближенное значение температуры образования карбонитрида Т:
T = 15200/(lg хTiN - A). (6.93)
Величина Т будет приближенной потому, что fTi , fN , а следовательно, и А зависят от температуры.
Оценив величину Т, можно, используя формулы (6.81) – (6.83), уточнить значения коэффициентов активности fN, fTi, fC. Повторив вычисления по формулам (6.87), (6.88) и (6.92), (6.93) с использованием уточненных значений fN , fTi и fC , получим более точные данные о составе карбонитридов (хTiC и хTiN) и температуре их образования Т. Для получения необходимой точности величин хTiC, хTiN и Т процесс вычислений повторяют несколько раз.
Для анализа факторов, влияющих на состав карбонитридов (хTiC /хTiN), разделим уравнение (6.78) на (6.79). После логарифмирования и подстановки значений lg K1 и lg K2 получим
lg(хTiC/хTiN) = lg(aC /aN) - 7100/T + 0,8. (6.94)
Из выражения (6.94) видно, что при увеличении аC/аN и повышении температуры образования карбонитридов доля TiC в них увеличивается. При постоянном аC/аN температура образования карбонитридов и соответственно доля TiC в них может быть увеличена в результате повышения активности титана аTi в металле.
Решение. 1. Вычислим значения логарифмов fN, fTi, fC при 1873 К, использовав соответствующие параметры взаимодействия (см. задачу 61). Получим lg fN(1873) = -1,28; lg fTi (1873) = 1,16; lg fC (1873) = -0,66.
2. Оцениваем состав карбонитридов (хTiC и хTiN) и температуру их образования в первом приближении, считая fN = fN(1873), fTi = fTi (1873), fC = fC(1873).
По формулам (6.87) и (6.88) вычислим коэффициенты А и В:
A = lg (0,7×0,08) + 1,16 - 1,28 - 5,6 = -7,0;
В = lg (0,7×0,13) + 1,16 - 0,66 - 4,8 = -5,34.
Подставив А и В в уравнение (6.92), получим
хTiC = [ехр(2,3(-5,34 + 0,533×7,0))](1 - хTiC)0,533
или
хTiC = 0,025(1 - хTiC)0,533. (6.95)
Исследуем полученное уравнение на возможность решения методом итераций (сходимость итераций). Производная правой части уравнения j(хTiC) = 0,025(1 - хTiC)0,533 равна j¢(хTiC) = -0,0133(1 -
– хTiC)-0,467. Значение j¢(хTiC) < 1 в интервале от хTiC = 0 до хTiC = 0,999. Следовательно, в данном интервале итерации сходятся. Вычислим корень уравнения (6.92). Примем начальное значение корня (хTiC)0 = 0. Тогда последующие значения хTiC будут такие:
(хTiC)1 = 0,025(1 - 0)0,533 = 0,025;
(хTiC)2 = 0,025(1 - 0,025)0,533 = 0,02466;
(хTiC)3 = 0,025(1 - 0,02466)0,533 = 0,02467.
В качестве корня уравнения (6.92) принимаем хTiC = 0,025. Соответственно хTiN = 1 - 0,025 = 0,975.
Температура образования карбонитрида, вычисленная по формуле (6.93),
Т = 15200/[lg0,975 - (-7,0)] = 2174 К.
3. Учтем зависимость fN, fTi, fC от температуры, используя формулы (6.81) – (6.83). Для 2174 К lgfN = -0,97; lgfTi = 0,94; lgfC = -0,54. Значения коэффициентов А = -6,88, В = -5,44. Подставив А и В в уравнение (6.92), после преобразований получим хTiC = 0,017(1 - хTiC)0,533. Корень полученного уравнения хTiC = 0,01685 » 0,017; хTiN = = 1 - 0,017 =
= 0,983. Соответственно уточненная температура образования карбонитридов Т = 2212 К. Следующее уточнение fN , fTi , fC дает
хTiC = 0,01715 » 0,017; хTiN = 0,983 и T = 2208 К. При дальнейших итерациях значения хTiC , хTiN и Т практически не изменяются. Значение температуры образования нитридов TiN вычислим по формуле (6.93) при хTiN = 1. Получим TTiN = 2206 К. Таким образом, в стали данного состава карбонитриды (хTiC = 0,017 и хTiN = 0,983) могут образовываться при 2208 К. Отметим, что состав карбонитридов близок к TiN. Температуры образования карбонитридов (2208 К) и нитридов (2206 К) также практически совпадают.
4. Оценим изменение состава карбонитридов и условия их выделения при охлаждении стали. Из полученных выше результатов следует, что при охлаждении металла выделяется практически чистый TiN. Балансовым расчетом можно показать, что, например, при 1773 К в растворе останется 0,0035 % [N] и 0,44 % [Ti]. При таком составе металла должны выделяться карбонитриды с хTiC = 0,1. Температура их образования равна 1790 К, т.е. на 17 К выше температуры 1773 К, соответствующей равновесию с чистым нитридом. Таким образом, из расчета видно, что состав карбонитридов, образующихся в жидкой стали 15Х25Т, близок к составу нитридов, и условия их существования с достаточной для практики точностью могут быть оценены при допущении образования чистых нитридов.
65. Микролегирование стали азотом
и нитридообразующими элементами
Задача. Определить концентрации азота и титана для микролегирования стали 12Х17.
Исходные данные. Содержание в стали 12Х17 основных элементов: 0,12 % С; 17 % Сr.
Теория. Для повышения качества ряда сталей (конструкционных, коррозионно-стойких, быстрорежущих) в их состав часто вводят азот и нитридообразующие элементы. При этом вследствие образования мелкодисперсных нитридов повышается прочность стали, измельчается исходное зерно аустенита, снижается чувствительность стали к росту зерна при нагреве. В результате измельчения зерна повышается ударная вязкость и понижается температурный порог хладноломкости. Положительное влияние нитридов на качество металла проявляется не при всех концентрациях азота и нитридообразуюших элементов, а при определенных, характерных для данной марки стали концентрациях. Эти концентрации часто называют рациональными [N]р и [R]р (или оптимальными [44]), так как при них обеспечивается наилучший эффект от микролегирования.
Если провести большое число экспериментов, то для заданной марки можно определить рациональные значения [N]р и [R]р . Целенаправленность такого поиска для других сталей и уменьшение объема необходимых экспериментальных данных может обеспечить методика предварительной расчетной оценки значений [N]р и [R]р [44, 45]. Авторы [44, 45] предполагают, что размер, форма и другие характеристики нитридов, влияющие на свойства стали, зависят в первую очередь от температуры, при которой начинают образовываться нитриды. Такое допущение было сделано, в частности, в связи с тем, что при изменении [R] и [N] изменяется равновесная температура образования нитридов. Соответственно ей должна изменяться (при достаточно медленном охлаждении) и фактическая температура выделения нитридной фазы. Действительно, реакция образования, например, нитридов титана имеет вид (см. задачу 61)
[Ti] + [N] = TiN(т) ; (6.96)
lg К = lg(1/[Ti] fTi [N] fN) = (15200/T) - 5,6, (6.97)
откуда равновесная температура образования нитридной фазы
T = 15200/[lg(l/([Ti][N]/fTi fN)) + 5,6]. (6.98)
Из выражения (6.98) видно, что Т пропорциональна произведению [Ti][N]. Тогда рациональным значениям [R]р и [N]р должна отвечать некоторая рациональная температура образования нитридов Т.
Рациональность (оптимальность) температуры Т можно понимать следующим образом. Если концентрации [R] и [N] так велики, что нитриды образуются при высоких температурах, особенно до завершения кристаллизации, то следует ожидать выделения достаточно крупных включений и отрицательного их влияния на качество стали. Образуясь при низких температурах (малых [R] и [N]), включения могут не успеть выделиться из твердого металла и не дать ожидаемого эффекта. Следовательно, должна существовать рациональная температура, при которой образующиеся нитриды имеют благоприятные размеры, форму и другие характеристики, обеспечивающие повышение качества стали. Расчет фактических температур образования нитридов в реальных условиях осложняется трудностью учета ряда кинетических факторов. Эти трудности можно устранить, если использовать температуры, определяемые термодинамическим расчетом. Зная для некоторой стали экспериментально подобранные рациональные значения [N]р.и и [R]р.и, по формуле типа (6.98) рассчитываем рациональную температуру Tр.и (индекс «и» означает, что величины известны). Учитывая температурную зависимость fTi и fN (см. задачу 64) и преобразуя выражение (6.98), для случая микролегирования стали титаном получаем
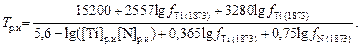 (6.99)
(6.99)
Допустим, что для другой стали с неизвестными значениями [N]р и [R]р рациональная температура образования нитридов равна Тр.и Тогда для определенной таким образом температуры Т можно рассчитать соответствующую ей область значений [N]р и [R]р в изучаемой стали. В частности, для рассматриваемого случая из уравнения (6.98) при учете температурной зависимости fTi и fN (см. задачу 64) следует
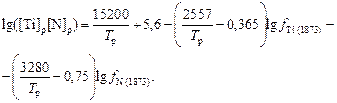 (6.100)
(6.100)
Правильность допущения Tр = Тр.и подтверждена [45] постоянством значений Тр.и для каждого вида нитридов и разных по классу сталей. Для 70 %-ной вероятности значения Тр.и попадают в следующие интервалы: ТZrN = 1515 ± 26 °С; ТTiN = 1388 ± 30 °С; ТAlN = 1370 ± 50 °С;
ТVN = 703 ± 55 °С. Таким образом, зная Тр.и для каждого из нитридов, можно оценить рациональные концентрации нитридообразующих элементов в искомых сталях. Для определения рациональной температуры образования нитридов титана в стали 12Х17 используем известные для стали 15ХГН2ТА (0,15 % С; 1 % Сr; 1 % Мn; 1,5 % Ni) значения рациональных концентраций титана (0,05 %) и азота (0,01 %) [46].
Решение. 1. Определим рациональную температуру образования нитридов титана в стали 15ХГН2ТА.
Используя параметры взаимодействия, вычислим значения lg fN и lg fTi при 1873 К:
lg fN (1873) = -0,08, lg fTi (1873) = -0,04.
Подставив значения [Ti]р.и. = 0,05 %; [N]р.и. = 0,01 %; lg fN(1873) =
= -0,08; lg fTi (1873) = -0,04 в уравнение (6.100), получим
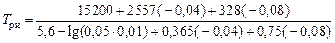 = 1681 К.
= 1681 К.
2. Определим рациональные концентрации азота и титана в стали 12Х17. Вычислим значения lg fN и lg fTi при 1873 К по параметрам взаимодействия:
lgfN(1873) = -0,67; lgfTi(1873) = 0,28.
Подставив значения Тр = Тр.и = 1681 К; lg fN(1873) = -0,67; lg fTi(1873) = = 0,28 в уравнение (6.100), получим
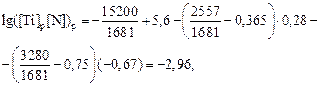
т.е. [Ti]р[N]р = 0,0011 = const .
Видно, что рациональная концентрация титана в стали определяется содержанием азота. Например, при [N] = 0,01 % величина [Ti] = = 0,11 %, а при [N]р = 0,1 % [Ti]р = 0,011 %. При обычных для стали 12Х17 содержаниях азота (0,03–0,06 %) рациональные концентрации титана равны 0,02–0,04 %. Эти рекомендации неплохо согласуются с практикой. На ряде заводов инструкции на выплавку сталей 12Х17 и 15Х28 предусматривают введение 0,1–0,2 % Ti без учета угара и расхода на раскисление стали. Титан вводят как технологическую присадку для измельчения зерна и повышения пластичности металла при прокатке. Таким образом, изложенная в задаче методика позволяет достаточно правильно оценивать концентрации азота и нитридообразующих элементов для микролегирования сталей.
7. Раскисление стали
66. Раскисление стали алюминием
Задача. После проведения окислительного периода в ДСП железоуглеродистый расплав содержит 0,1 % углерода. Температура металла 1600 °С. Термодинамическим расчетом определить концентрацию кислорода в металле после раскисления его алюминием. Остаточная концентрация алюминия в растворе – 0,02 %. Определить также количество включений Al2O3 % масс, образовавшихся при раскислении металла. Как изменится эта величина при охлаждении расплавa до 1550 °С?
Принять, что компоненты металла образуют идеальный разбавленный раствор.
Исходные данные
1. 2Al 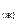 +
+ 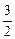 O
O 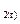 = Al
= Al 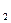 O
O 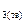 ; (7.1)
; (7.1)
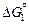 = –1676110 + 320,08 T, Дж/г-ат.
= –1676110 + 320,08 T, Дж/г-ат.
2. Al 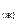 = Al(1% в Fe);
= Al(1% в Fe);
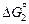 = –62760 – 23,85 T, Дж/г-ат. (7.2)
= –62760 – 23,85 T, Дж/г-ат. (7.2)
3.  O
O 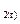 = [O](1% в Fe); (7.3)
= [O](1% в Fe); (7.3)
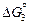 = –117150 – 2,89 T, Дж/г-ат.
= –117150 – 2,89 T, Дж/г-ат. 
Теория. При обезуглероживании расплава в открытой печи 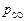 = 0,101 МПа (1 атм). Следовательно, при 1600 °С произведение [C] × [O] = 0,0025(%)2. Отсюда начальная (перед раскислением) концентрация кислорода в металле
= 0,101 МПа (1 атм). Следовательно, при 1600 °С произведение [C] × [O] = 0,0025(%)2. Отсюда начальная (перед раскислением) концентрация кислорода в металле
[O] 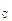 =
= 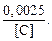

Для отыскания концентрации кислорода в металле после раскисления удобно записать реакцию раскисления таким образом, чтобы алюминий и кислород участвовали в ней в растворенном состоянии:
2[Al](1%) + 3[O](1%) = Al2O3 (тв). (7.4)
Тогда
K 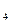 =
= 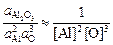 ,
,
откуда
[O] 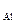 =
= 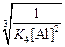 . (7.5)
. (7.5)
Значение K4 найдем из выражения
lg K4 = – 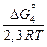 . (7.6)
. (7.6)
Величину 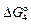 можно вычислить, комбинируя уравнения реакций (7.1) – (7.3):
можно вычислить, комбинируя уравнения реакций (7.1) – (7.3):
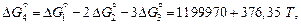 Дж/моль.
Дж/моль.
Количество включений Al2O3 (%) при 1600 и 1550 °С определим по формулам
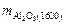 =
= 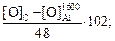 (7.7)
(7.7)
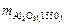 =
= 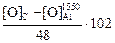 , (7.8)
, (7.8)
где 102 – молекулярная масса Al2O3;
48 – атомная масса кислорода в Al2O3.
Решение
Температура 1600 °С
Найдем начальную концентрацию кислорода.
[O]С = 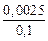 = 0,025 %.
= 0,025 %.
Вычислим K4 по формуле (7.6):
lg K4 = – 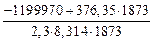 = 13,83 ; K4 = 6,75
= 13,83 ; K4 = 6,75  1013.
1013.
Определим [O] 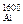 по формуле (7.5):
по формуле (7.5):
[O] 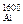 =
= 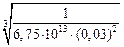 = 0,00025 %.
= 0,00025 %.
Количество включений Al2O3 при 1600 °С
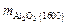 =
= 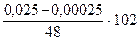 = 0,0526 %.
= 0,0526 %.
Температура 1550 °С
Вычислим K4 по уравнению (7.6):
lgK4 = – 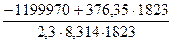 = 14,75; K4 = 5,6 · 10
= 14,75; K4 = 5,6 · 10 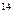 .
.
Найдем [O] 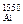 по формуле (7.7):
по формуле (7.7):
[O] 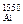 =
= 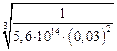 = 0,000125 %.
= 0,000125 %.
Определим 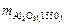 по уравнению (7.8):
по уравнению (7.8):
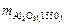 =
= 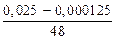 · 102 = 0,0529 %.
· 102 = 0,0529 %.
Итак, концентрация кислорода в металла после раскисления его алюминием составляет 0,00025 %. Количество образовавшихся при этом включений Al2O3 равно 0,0526 %. При охлаждении металла с 1600 до 1550 °С оно увеличилось до 0,0529 %.
67. Ряд раскислителей
Задача. Найти место углерода в ряду раскислителей Mn, Si, Al для трех случаев: a) рCO = 101 кПа (1 атм); б) рCO = 10,1 кПа (0,1 атм) и в) рCO = 0,1 кПа (0,001 атм). Остаточные концентрации раскислителей в растворе равны 0,1 %. Температура 1600 °С.
Принять, что компоненты металла образуют идеальный разбавленный раствор, а продуктом раскисления являются чистые оксиды.
Исходные данные
1. [Mn] + [O] = MnO(тв); lg K1 = 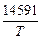 – 6,045. (7.9)
– 6,045. (7.9)
2. [Si] + 2[O] = SiO2(тв); lg K2 = 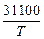 – 12,0. (7.10)
– 12,0. (7.10)
3. 2Al + 3[O] = Al2O3(тв); lg K3 = 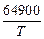 – 20,63. (7.11)
– 20,63. (7.11)
4. [C] + [O] = CO(г); lg K4 = 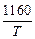 + 2,0. (7.12)
+ 2,0. (7.12)
Теория. Равновесные концентрации кислорода ([O]) в металле при раскислении жидкой стали указанными элементами можно найти по формулам
[O]Mn = 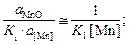 (7.13)
(7.13)
[O]Si = 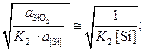 (7.14)
(7.14)
[O]Al = 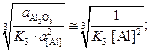 (7.15)
(7.15)
[O]C = 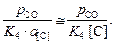 (7.16)
(7.16)
Сравним результаты расчета [O], определим положение углерода в ряду указанных раскислителей.
Решение
lg K1 = 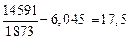 ; K1 = 56.
; K1 = 56.
lg K2 = 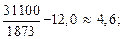 K2 = 4 · 104.
K2 = 4 · 104.
lg K3 = 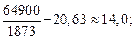 K3 » 1014.
K3 » 1014.
lg K4 = 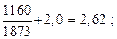 K4 = 416.
K4 = 416.
[O]Mn = 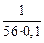 = 0,18 %;
= 0,18 %;
[O]Si = 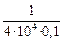 = 0,016 %;
= 0,016 %;
[O]Al = 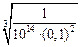 = 0,0001 %.
= 0,0001 %.
Случай а): [O]C = 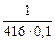 = 0,024 %.
= 0,024 %.
Видно, что при рCO = 1 атм углерод можно поставить в ряду раскислителей между марганцем и кремнием: Mn, C, Si, Al.
Случай б): [O]C = 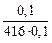 = 0,0024 %.
= 0,0024 %.
При рCO = 0,1 атм углерод становится между кремнием и алюминием: Mn, Si, C, Al.
Случай в): [O]C = 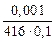 = 0,000024 %,
= 0,000024 %,
т.е. при рCO = 0,001 атм углерод имеет уже более высокую раскислительную способность, чем алюминий: Mn, Si, Al, C.
68. Раскисление стали кремнием и марганцем
Задача. Определить равновесное содержание кислорода в стали 14Г, раскисленной кремнием и марганцем, остаточные концентрации которых равны соответственно 0,2 и 1,0 %. Принять, что продукты раскисления и компоненты стали образуют идеальные растворы. Сравнить полученные результаты с данными по раскислению металла только кремнием с образованием SiO2 (тв). Температура 1600 °С. Термодинамическим влиянием концентрации углерода пренебречь.
Исходные данные
[Mn] + [O] = (MnO), lg K1 = 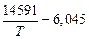 ; (7.17)
; (7.17)
[Si] + 2[O] = (SiO2), lg K2 = 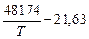 . (7.18)
. (7.18)
Теория . Запишем систему уравнений, решив которую, найдем концентрацию кислорода ([O]Si – Mn), равновесную с кремнием, марганцем и раствором их оксидов.

откуда
[O] 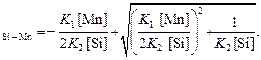 (7.22)
(7.22)
При раскислении стали только кремнием концентрацию кислорода ([O]) можно вычислить из уравнения (7.20), учтя, что
х 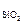 = 1.
= 1.
[O] 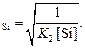 (7.23)
(7.23)
Решение
lg K1 = 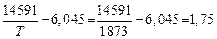 ; K1 = 56.
; K1 = 56.
lg K2 = 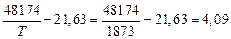 ; K2 = 1,23 · 104.
; K2 = 1,23 · 104.
[O] 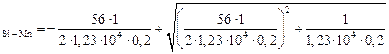 =
=
= 0,0116 % 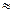 0,012 %;
0,012 %;
[O] 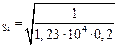 = 0,020 %.
= 0,020 %.
Ответ. Расчет показывает, что добавка слабого раскислителя (марганца) к кремнию обеспечивает более глубокое раскисление стали ([O] 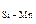 = 0,012 %) по сравнению с присадкой только кремния ([O]
= 0,012 %) по сравнению с присадкой только кремния ([O] 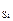 = 0,020 %). Это связано со снижением активности SiO2 (
= 0,020 %). Это связано со снижением активности SiO2 ( 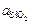 < 1) при комплексном раскислении. В частности, в данном случае
< 1) при комплексном раскислении. В частности, в данном случае 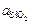 = х
= х 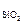 = K2 [Si] [O]
= K2 [Si] [O] 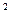 = 1,23 · 0,2 · 104 · (0,012)2
= 1,23 · 0,2 · 104 · (0,012)2 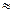 0,35.
0,35.
69. Расчет кривой раскисления
по активности кислорода в стали
Задача. По экспериментальным данным об изменении активности кислорода в зависимости от концентрации алюминия в стали 12Х17, полученным при измерении активометром, построить кривую раскисления и определить, при каком остаточном содержании алюминия в стали концентрация растворенного кислорода минимальна.








