5. Кислород и углерод в стали. обезуглероживание высоколегированных расплавов
46. Обезуглероживание
высокохромистого расплава
Задача. Расплав Fе–Cr–Ni продувают кислородом в открытой электродуговой печи. Вычислить конечную концентрацию углерода, которую можно получить до начала интенсивного окисления хрома при 1973 К. Определить изменение этой концентрации углерода: 1) при повышении температуры до 2173 К; 2) при уменьшении давления образующегося оксида углерода до 10 кПа (в случае разбавления ее аргоном или проведения продувки в вакууме).
Исходные данные, рекомендуемые допущения. Концентрация легирующих в расплаве: 10 % [Cr], 10 % [Ni]. Влиянием [% С] на fC пренебречь. Температурную зависимость коэффициента активности оценить, используя ТРР: lgfC(T ) = 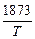 lgfC(1873) (см. задачу 19).
lgfC(1873) (см. задачу 19).
Теория. Окисление углерода и хрома в расплавах, содержащих более 9 % хрома, описывается следующими уравнениями [3]:
Сr3O4(т) + 4[С] = 3[Cr] + 4СО(г); (5.1)
DG = 882500 - 585T, Дж ; (5.2)
lgK1/4 = lg([Cr]3/4 pCO /fC [C]) = -(11520/T ) + 7,64. (5.3)
В уравнении (5.3) принято aCr3O4 = 1 в связи с тем, что при обезуглероживании высокохромистых расплавов образуются вязкие (гетерогенные) шлаки, насыщенные оксидами хрома.
Если при продувке кислородом начальная концентрация углерода выше равновесной, определенной из уравнения (5.3), то в ходе продувки окисляется в основном углерод. После снижения содержания углерода до равновесного углерод и хром будут окисляться совместно таким образом, что соотношение между ними будет определяться уравнением (5.3). Угар хрома при этом будет значительно выше, чем при более высоких содержаниях углерода (выше равновесного).
Поскольку окисление хрома кислородом сопровождается значительным выделением тепла, температура ванны повышается и, как видно из уравнения (5.3), это приводит к увеличению отношения [Сr]3/4/[С]. Для практических расчетов пользуются отношением [Cr]/[С].
Влияние давления монооксида углерода на равновесное состояние реакции (5.1) также определяется уравнением (5.3). Величина рCO здесь выражается в атмосферах (1 атм = 101,325 кПа), так как стандартное давление в термодинамических справочниках принимают равным 1 атм.
Решение. 1. Определим из уравнения (5.3) равновесное содержание углерода (при 10 % [Cr], 10 % [Ni], рCO = 1 атм, Т = 1973 К). Коэффициент активности fC(1873) определяем с помощью параметров взаимодействия первого и второго порядка (см. табл. П3 – П5). Влиянием [С] на fC пренебрегаем.
lg fC (1873) = -0,12;
lg fC (1973) = (1873/1973)(-0,12) = -0,114;
lg fC (2173) = (1873/2173)(-0,12) = -0,103.
Как видно, температурная поправка сравнительно мала, поэтому погрешность, связанная с использованием ТРР, невелика.
lg[С]T = 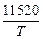 -7,64 +
-7,64 + 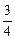 lg[Cr] + lg pCO - lg fC (T ).
lg[Cr] + lg pCO - lg fC (T ).
При pCO = 1 атм
lg [C](1973) = -0,937; [C](1973) = 0,116 %;
lg[С](2173) = -1,4856; [С](2173) = 0,033 %.
При pCO = 10/101,325 » 0,1 атм
lg[С](1973) = -1,937; [С](1973) = 0,0116 %.
Таким образом, при 1973 К и pCO = 1 атм без значительного угара хрома можно получить [С] = 0,12 %. Повышение температуры до 2173 К снижает эту величину до 0,03 %, а понижение pCO до 0,1 атм уменьшает [С] до 0,012 %.
Примечание. В справочных таблицах обычно отсутствуют данные по оксиду Cr3O4, так как его образование в рассматриваемом процессе – это только гипотеза, хотя и хорошо согласующаяся с опытами. Большинство расчетов можно выполнить вполне удовлетворительно и при допущении образования (Cr2O3).
47. Равновесие расплава Fe–C
с окислительными шлаками
Задача. Шлак окислительного периода с мольной долей 20 % FeO. Вычислить концентрацию углерода в расплаве Fe–С, находящемся в равновесии со шлаком при 1873 К. Принять, что металл и шлак - идеальные растворы.
Исходные данные [3]:
1. [О] + Fe(ж) = FeO(ж) ; 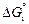 = -121000 + 52,4Т, Дж/моль. (5.4)
= -121000 + 52,4Т, Дж/моль. (5.4)
2. [С] + [О] = СО(г) ; 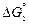 = -22400 - 39,7 T, Дж/моль. (5.5)
= -22400 - 39,7 T, Дж/моль. (5.5)
Теория. Рассмотрим равновесие реакции, результирующей реакций (5.4) и (5.5):
[С] + FeO(ж) = СО(г) + Fe(ж) ; (5.6)
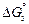 =
= 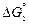 -
- 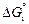 = 98600 - 92,1Т, Дж/моль;
= 98600 - 92,1Т, Дж/моль;
K3 = pCO/([C]fC aFeO). (5.7)
Металл и шлак - идеальные растворы, т.е.
aFeO = xFeO » (% FeO)/100 и fC = 1,
откуда
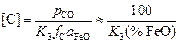 . (5.8)
. (5.8)
Решение. Вычислим значение константы равновесия реакции (5.6) при 1873 К:
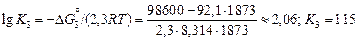 . (5.9)
. (5.9)
Тогда концентрация углерода в металле, находящемся в равновесии со шлаком, в соответствии с формулой (5.8) равна
[С] = 100/(115×20) = 0,043 %.
Примечания. 1. Видно, что решение задачи дано по сумме реакций (5.4) и (5.5). В тех случаях, когда кроме [С] необходимо определить активность кислорода, соответствующую равновесию со шлаком, можно воспользоваться выражением константы равновесия реакции (5.4):
K1 = aFeO /aO = xFeO /[O],
откуда
[О] = xFeO /K1 = 0,20/4,36 = 0,046 %.
Зная [О], из равновесия реакции (5.5) можно легко найти равновесное со шлаком содержание углерода [С]:
[С] = pCO /(K2[O]fOfС) » 1/(K2[О]) = 1/(500×0,046) = 0,043 %.
2. Пусть в качестве исходных данных имеем не DG º реакций
(5.4) – (5.6), а предельную растворимость кислорода в железе [О]max = 0,23 % и произведение равновесных содержаний [С] и [О] при pCO = 1 атм, составляющее [С]×[О] = 0,0020, тогда K1 = aFeO /aO »
» xFeO /[O].
При xFeO = 1 [O] = [О]max = 0,23 % и K1 = 1/[О]max = 1/0,23.
Соответственно под шлаком с заданным содержанием FeO
[О] = xFeO /K1 = [О]max × xFeO = 0,23×0,2 = 0,046 %.
Соответственно [С] = 0,0020/0,046 = 0,043 %.
3. Использовав выражение К3 , можно решить и обратную задачу: определить активность FeO в шлаке, равновесном с углеродсодержащим расплавом данного состава при заданных температуре и pCO: aFeO = pCO /(K3 [С]fC ).
48. Термодинамика обезуглероживания металла с учетом одновременного образования СО и СО2
Задача. Определить равновесное содержание кислорода в металле [% О] и {% СО2} в газовой фазе при глубоком обезуглероживании железа (менее 0,05 % С) в зависимости от давления. Определить поправку, которую вносит в результаты расчетов учет образования СО2 .
Исходные данные. 1. Температура T = 1873 К. 2. Принять два значения давления (р = pCO + pCO2): p1 = 1 атм; p2 = 0,1 атм.
Теория. Из реакции
[С] + [О] = СО(г) ; DGº = -22400 - 39,7T, Дж (5.10)
следует
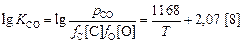 . (5.11)
. (5.11)
Пренебрегая влиянием малых концентраций углерода на fC и fO , получаем
lg (fC fO ) = 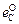 [О] +
[О] + 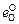 [O] = -(0,34 + 0,20)[О] = -0,54 [О]. (5.12)
[O] = -(0,34 + 0,20)[О] = -0,54 [О]. (5.12)
Для приближенной оценки [О] воспользуемся соотношением (5.11), приняв Т = 1873 К, fC fO = 1, pCO = p (pCO2 = 0) и учтя, что при р = 1 атм m = [С][О] = 1/kCO = 0,002. Получим
[О] = 0,002р/[С] . (5.13)
Из уравнений (5.11) – (5.13) получим
lg[O] = 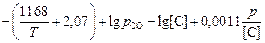 . (5.14)
. (5.14)
Чтобы найти DGº для реакции окисления [С] с образованием СO2 , воспользуемся данными [8] о следующей совокупности реакций:
[С] + [О] = СО(г) , DGº = -22400 - 39,7Т Дж;
С(гр) + О2 (г) = СО2(г) , DGº = -397000 + 0,2T Дж;
СО(г) = С(гр) + 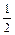 O2(г) , DGº = 118000 + 83,77T Дж;
O2(г) , DGº = 118000 + 83,77T Дж;
[О] =  O2(г) DGº = 117000 + 2,89T Дж
O2(г) DGº = 117000 + 2,89T Дж
__________________ __________________________
[С] + 2[O] = СO2 (г) ; DGº = -183600 + 47,16T Дж, (5.15)
откуда
lg KCO2 = lg[pCO2 /(fC [C] 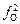 [О]2)] = (9600/T ) - 2,464. (5.16)
[О]2)] = (9600/T ) - 2,464. (5.16)
По аналогии с выражением (5.12):
lg (fC 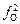 ) = -(0,34 + 2×0,2)[O] = -0,74[O]. (5.17)
) = -(0,34 + 2×0,2)[O] = -0,74[O]. (5.17)
Подставив в выражение (5.16) формулу (5.17) и оценку [О] по соотношению (5.13), найдем
lg [О] = - 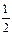 [(9600/T) - 2,464] +
[(9600/T) - 2,464] + 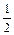 lgpCO2 -
lgpCO2 - 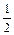 lg[С] +
lg[С] +
+ 0,00074(p/[С]). (5.18)
Правые части уравнений (5.14) и (5.18) можно приравнять, поскольку они равны порознь одной и той же величине. После преобразования получим
lg (pCO / 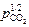 ) = -(3589/T ) + 3,279 +
) = -(3589/T ) + 3,279 + 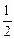 lg[С] - 0,00036(p/[C]) . (5.19)
lg[С] - 0,00036(p/[C]) . (5.19)
Из выражения (5.19) можно определить величину lg (pCO / 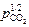 ) для любых заданных [С], T и р. Далее, учитывая, что pCO + pCO2 = p и рeшaя соответствующее квадратное уравнение, можно определить pCO и pCO2 , а также искомое содержание СО2 в газовой фазе {% СО2 } =
) для любых заданных [С], T и р. Далее, учитывая, что pCO + pCO2 = p и рeшaя соответствующее квадратное уравнение, можно определить pCO и pCO2 , а также искомое содержание СО2 в газовой фазе {% СО2 } =
= (pCO2 /p)100.
Чтобы найти равновесное содержание кислорода в металле, можно воспользоваться соотношением (5.14) или (5.18).
Поправку, вносимую учетом СО2 , определим, сравнив полученные данные с результатами расчетов по уравнению (5.14) при pCO = p.
Решение. Определим для примера [О] и {% СО2 } при [С] = 0,05 %, Т = 1873 К и р = 1 атм. Из уравнения (5.19) получим
lg (pCO / 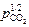 ) =
) = 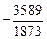 + 3,279 +
+ 3,279 + 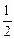 (-1,301) - 0,00036
(-1,301) - 0,00036 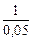 = 0,7051,
= 0,7051,
откуда
pCO = 1 - pCO2 = 5,071 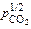
или
( 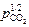 )2 + 5,071(
)2 + 5,071( 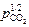 ) - 1 = 0.
) - 1 = 0.
Решив квадратное уравнение, найдем
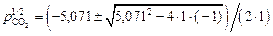 .
.
Имеет смысл только один корень 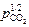 = 0,19. Таким образом,
= 0,19. Таким образом,
pCO2 = 0,036, { % СО2} = 3,6.
Подставив значение pCO2 в выражение (5.18), получим
lg [О] = - 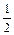 [(9600/1873) - 2,464] +
[(9600/1873) - 2,464] + 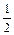 (-1,4437) -
(-1,4437) - 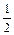 (-1,301) +
(-1,301) +
+ 0,00074(1/0,05) = -1,3873; [O] = 0,041 %.
Результаты аналогичных расчетов для других условий приведены в таблице.
| [С], % | р = 1 атм | р = 0,1 атм | ||
| {CO2 , %} | [O], % | {CO2 , %} | [O], % | |
| 0,05 | 3,6 | 0,041 | 0,4 | 0,013 |
| 0,03 | 5,9 | 0,069 | 0,6 | 0,021 |
| 0,01 | 15,8 | 0,22 | 2,1 | 0,069 |
| 0,004 | - | - | 4,5 | 0,163 |
| 0,002 | - | - | - | - |
Прочерки означают невозможность достижения указанных очень малых значений [С] в заданных условиях. Расчетное значение равновесного [О] для этих условий превышает предел растворимости (0,23 % при 1873 К).
Как видно из приведенных данных, доля СО2 в продуктах окисления углерода при малых [С] может быть существенной.
Рассчитаем для сравнения равновесное значение [О] при [С] = 0,01 % (Т = 1873 К, р = 1 атм) без учета СО2 . Из выражения (5.14), полагая pCO = p = 1 атм, находим
lg [O] = 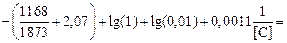 -0,5386;
-0,5386;
[O] = 0,261 %.
Полученная величина существенно выше приведенной в таблице (0,22 %) и превосходит предел растворимости кислорода. Таким образом, обезуглероживание до [C] = 0,01 % в указанных условиях оказывается невозможным, если вести расчет без учета СО2 . Если учитывать образование СО2 , то расчет указывает на возможность удаления углерода до 0,01 %.
Примечание. Отметим, что влияние СО2 уменьшается при увеличении [С] и уменьшении общего давления (pCO + pCO2). Предельное равновесное содержание СО2 в газовой фазе можно рассчитать по реакции
FeO(ж) + СO(г) = СO2 (г) + Fe(ж) .
49. Раскисление металла углеродом
в электродуговой печи при повторном кипении после продувки кислородом
Задача. В ряде случаев при выплавке стали в дуговых печах для предварительного раскисления металла после продувки кислородом в расплав вводят чугун. Это сопровождается интенсивным повторным кипением.
При выплавке электротехнической стали введение 1,5 % чугуна в металл с 0,03 % С не вызывает увеличения содержания углерода. Определить степень переокисленности расплава перед этой операцией (после продувки кислородом) и долю растворенного кислорода, удаляемого в виде СО.
Исходные данные и рекомендуемые допущения. 1. Принять, что содержание кислорода после повторного кипения соответствует равновесию с углеродом. 2. Считать, что шлак во взаимодействии с чугуном не участвует. 3. Чугун содержит 4,3 % С; 0,7 % Si. Принять, что кремний полностью идет на раскисление (участием марганца чугуна в раскислении пренебречь). 4. Температура расплава до введения чугуна 1968 К, после введения – 1943 К. В связи с тем что константа реакции обезуглероживания сравнительно слабо зависит от температуры, для расчетов можно принять среднее значение Т = 1955 К.
Теория. Для установления степени переокисленности исходного расплава 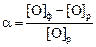 ×100 % необходимо определить равновесную концентрацию кислорода [О]р и сопоставить ее с фактической [O]ф , которая больше равновесной на количество кислорода, связываемое углеродом и кремнием чугуна. Для реакции
×100 % необходимо определить равновесную концентрацию кислорода [О]р и сопоставить ее с фактической [O]ф , которая больше равновесной на количество кислорода, связываемое углеродом и кремнием чугуна. Для реакции
[С] + [О] = СO(г) (5.20)
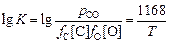 + 2,07 [8]. (5.21)
+ 2,07 [8]. (5.21)
Для условий открытой плавки pCO » 1 атм. Для определения равновесной концентрации кислорода в условиях данной задачи можно на первом этапе принять коэффициенты активности равными 1. Влиянием углерода на эти коэффициенты можно пренебречь в связи с тем, что его массовая доля мала. Влияние кислорода на fC и fO должно быть оценено после предварительного расчета (методом итераций) с учетом параметров взаимодействия по уравнениям
lg fO = 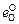 [O] = [(-1750/T ) + 0,734][О] ; (5.22)
[O] = [(-1750/T ) + 0,734][О] ; (5.22)
lg fC = 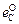 [O] = -0,34[О]*, (5.23)
[O] = -0,34[О]*, (5.23)
откуда
lg (fCfO) = [(-1750/T ) + 0,394][О]. (5.24)
Количество кислорода, связанного углеродом и кремнием, определяется из стехиометрических соотношений:
при образовании СО расход кислорода превышает расход углерода в 16/12 = 1,33 раза;
при образовании SiO2 расход кислорода больше расхода кремния в 32/28 = 1,14 раза.
Решение. Найдем предварительное значение равновесной [О]р без учета fC и fO:
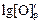 = - lg[С] - (1168/T ) - 2,07 = -1,145;
= - lg[С] - (1168/T ) - 2,07 = -1,145; 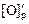 = 0,0715 %.
= 0,0715 %.
Согласно выражению (5.24)
lg(fC fO ) = [(-1750/1955) + 0,394]×0,0715 = -0,0358; fCfO = 0,92.
Уточненное значение [О]р равно:
lg[O]р = 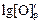 - lg(fC fO ) = -1,145 - (-0,0358) = -1,109; [O]р = 0,078 %.
- lg(fC fO ) = -1,145 - (-0,0358) = -1,109; [O]р = 0,078 %.
Углеродом чугуна связано кислорода 1,5×0,043×1,33 = 0,086 %, кремнием чугуна связано кислорода 1,5×0,007×1,14 = 0,012 %, отсюда [О]ф = 0,078 + 0,086 + 0,012 = 0,176 %. Степень переокисленности составит
a = [(0,176 - 0,078)/0,078 ]×100 = 126 %.
Доля кислорода, удаляемого в виде СО,
[О]CO / [O]ф = (0,086/0,176)×100 = 49 %.
50. Удаление водорода
при обезуглероживании металла
Задача. При обезуглероживании железа, содержащего водород, в пузырях СО наряду с молекулярным водородом (Н2) должно присутствовать некоторое количество водяного пара (Н2О). Определить с помощью термодинамического расчета, в какой форме происходит преимущественное удаление водорода из металла при обезуглероживании: Н2 или Н2О. Оценить в связи с этим влияние [O] и [С] на удаление водорода.
Исходные данные. Вычисления сделать для расплава с различными значениями [С] в интервале от 1,0 до 0,02 % при рCO = 1 атм и 1873 К. Принять т = [С][О] = 0,0025 %.
Теория. Наряду с общепринятым представлением об удалении водорода из металла при обезуглероживании в форме Н2 (г) существует мнение, что значительную роль при этом играет окисление водорода до Н2О(г) . На основе этого мнения К.Н. Ивановым была предложена технология получения стали с низким содержанием водорода, которая состоит в том, что металл сначала подвергают глубокому обезуглероживанию (до 0,04–0,10 %), добиваясь хорошего окисления водорода, а затем науглероживают в соответствии с маркой стали.
Для оценки соотношения рH2O /рH2 в пузырях монооксида углерода необходимо рассчитать равновесие одной из возможных в рассматриваемой системе реакций, протекающих с участием Н2 и Н2O. Примерами таких реакций являются следующие:
Н2 (г) + СО(г) = Н2О(г) + [С]; (5.25)
Н2 (г) + [О] = Н2О(г); (5.26)
2[Н] + [O] = Н2О(г); (5.27)
Н2 (г) + СО2 (г) = Н2О(г) +СО(г). (5.28)
При выборе уравнения реакции руководствуются соображениями удобства, это не влияет на результат расчета. В данном случае удобнее воспользоваться реакцией (5.25), поскольку она позволяет связать искомое соотношение рH2O /рH2 непосредственно с содержанием углерода в металле. Отметим, что выбор уравнения реакции никак не связан с механизмом реакции, с местом ее протекания и т.д. В термодинамическом расчете эти вопросы просто не рассматриваются. Выбирая реакцию (5.25), мы вовсе не утверждаем, что водород выделяется в виде Н2, а потом окисляется уже в газовой фазе монооксидом углерода. В равной степени вероятным является также механизм, описываемый уравнением (5.27).
Найдем DGº реакции (5.25) c помощью табл. П1 и П2:
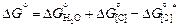 = -251070 + 57,65Т + 22600 -
= -251070 + 57,65Т + 22600 -
- 42,3Т + 118000 + 83,77Т = -110470 + 99,12Т Дж. (5.29)
Отсюда
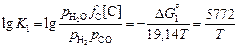 –5,179 (5.30)
–5,179 (5.30)
и, следовательно,
lg(рH2O /рH2 ) = (5772/T ) - 5,179 - lg fC - lg[C] + lg рCO . (5.31)
Решение. В таблице приведены результаты вычислений рH2O /рH2 для расплавов с различным содержанием углерода. Величина lg fC вычислена по формуле
lg fC = 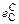 [С] +
[С] + 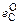 [О] = 0,14[С] - 0,34[О].
[О] = 0,14[С] - 0,34[О].
| [С], % | [O], % | lg fC | рH2O /рH2 | 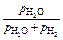 ×100 %** ×100 %**
|
| 1,0 | 0,0025 | 0,139 | 0,006 | 0,6 |
| 0,5 | 0,005 | 0,068 | 0,014 | 1,4 |
| 0,1 | 0,025 | 0,0055 | 0,078 | 7,2 |
| 0,04 | 0,625 | –0,016 | 0,205 | 17 |
| 0,02 | 0,125 | –0,042 | 0,436 | 30 |
Как видно из полученных результатов расчета, основную роль в процессе удаления водорода из металла в ходе обезуглероживания играет выделение в пузыри монооксида углерода молекул Н2 . Выделение Н2О увеличивается по мере снижения [С] (увеличения [О]), но даже при 0,02 % [С] доля Н2О более чем вдвое меньше доли Н2 .
51. Равновесие в системе Fе–С–О
Задача. Вычислить равновесную с углеродом концентрацию кислорода в жидкой стали при 1873 К и давлении 1 атм.
Исходные данные. 1. Состав стали: 0,18 % С; 2 % Сr; 4 % Ni.
2. Для реакции [С] + [О] = СО(г) :
DGº = -22400 - 39,7T Дж. (5.32)
Теория. Константа равновесия реакции (5.32) имеет вид
K = рCO /(aCaO ) = рCO/([C]fC[O]fO).
Тогда
[O] = рCO/(K[C] fCfO). (5.33)
Решение
lg К = -(DGº/2,3RT ) = –(-22400 - 39,7×1873)/(2,3×8,314×1873) » 2,7;
K = 500.
Определим fC и fO по параметрам взаимодействия (см. задачу 16):
lg fC = 0,14×0,18 - 0,024×2 + 0,012×4 = 0,025; fC = 1,06;
lgfO = -0,45×0,18 - 0,04×2 + 0,006×4 = -0,137; fO = 0,73.
Приняв, что рCO равно общему давлению над ванной металла (1 атм), найдем [О] по формуле (5.33):
[О] = 1/(500×0,18×1,06×0,73) = 0,015 %.
52. Активность кислорода в легированной стали
Задача. Найти, какой из элементов (углерод, марганец или хром) определяет активность кислорода в расплаве хромомарганцевой стали при окислительном рафинировании в открытой электродуговой печи.
Исходные данные. Жидкая сталь содержит: 0,10 % С; 14 % Сr; 6 % Мn.
Теория. При окислительном рафинировании расплава окисление углерода, хрома и марганца определяется следующими уравнениями:
[С] + [О] = СО(г) ; (5.34)
lg K1 = lg [рCO /(aCaO )] = (1168/T ) + 2,07;
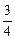 [Сr] + [О] =
[Сr] + [О] = 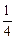 Cr3O4 (т) ; (5.35)
Cr3O4 (т) ; (5.35)
lg К2 = lg 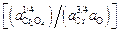 = (13380/T ) – 6,0;
= (13380/T ) – 6,0;
[Мn] + [О] = МnО(ж) ; (5.36)
lg К3 = lg [aMnO /(aMn aO)] = (12770/T ) – 5,7.
Если рCO = 1 атм, aCr3O4 = 1, aMnO = 1, то имеем
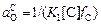 ; (5.37)
; (5.37)
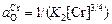 ; (5.38)
; (5.38)
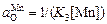 . (5.39)
. (5.39)
Если реакции (5.34) – (5.36) протекают независимо (т.е. могут иметь место частные равновесия), то окисленность aO определяется тем элементом (углеродом, хромом или марганцем), который обеспечивает наименьшее значение aO . В частности, если 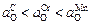 , то окисленность расплава определяется углеродом (aO =
, то окисленность расплава определяется углеродом (aO = 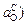 , который в данном случае проявляет наибольшее химическое сродство к кислороду. Отметим, что если достигается общее равновесие по всем элементам, то
, который в данном случае проявляет наибольшее химическое сродство к кислороду. Отметим, что если достигается общее равновесие по всем элементам, то 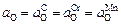 .
.
Решение. 1. Определим влияние содержания углерода на степень окисленности расплава при 1873 К. Константы равновесия реакций (5.34) – (5.36) равны: K1 = 494; К2 = 13,9; К3 = 13,1. Активности кислорода, равновесные с хромом и марганцем, вычислены по формулам (5.38) и (5.39):
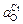 = 1/(13,9×143/4 ) = 0,010 %;
= 1/(13,9×143/4 ) = 0,010 %; 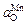 = 1/(13,1×6) = 0,013 %.
= 1/(13,1×6) = 0,013 %.
Величина fC , рассчитанная по параметрам взаимодействия, определяется выражением lgfC (1873) = 0,14[С] - 0,41.
Подставив величины fC и K1 в формулу (5.37), получим следующие значения в зависимости от содержания углерода:
| С, % | 1,0 | 0,45 | 0,10 |
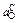 , % , %
| 0,004 | 0,010 | 0,050 |
Из сравнения значений 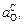
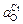 и
и 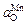 видно, что при [С] < 0,45 % окисленность расплава определяется хромом. При [С] > 0,45 % окисленность определяется углеродом. В этом случае возможно восстановление оксидов хрома и марганца углеродом.
видно, что при [С] < 0,45 % окисленность расплава определяется хромом. При [С] > 0,45 % окисленность определяется углеродом. В этом случае возможно восстановление оксидов хрома и марганца углеродом.
В рассматриваемом случае хром защищает марганец от окисления, так как химическое сродство к кислороду у хрома выше ( 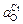 <
< 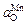 ).
).
2. Определим влияние температуры на окисленность расплава. Значения 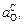
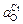 и
и 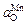 рассчитаем по тем же формулам, что и в пункте 1. Расчет fC при температурах, отличных от 1873 К, произведем по ТКР (см. задачу 19):
рассчитаем по тем же формулам, что и в пункте 1. Расчет fC при температурах, отличных от 1873 К, произведем по ТКР (см. задачу 19):
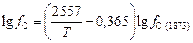 .
.
Результаты расчета при [С] = 0,1 % приведены в таблице.
| Т, K | K1 | K2 | K3 | fC | 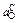
| 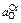
| 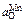
|
| 1873 | 494 | 13,9 | 13,1 | 0,40 | 0,05 | 0,01 | 0,013 |
| 1973 | 460 | 6,0 | 5,9 | 0,43 | 0,05 | 0,02 | 0,03 |
| 2073 | 430 | 2,8 | 2,9 | 0,46 | 0,05 | 0,05 | 0,06 |
| 2173 | 405 | 1,4 | 1,5 | 0,48 | 0,05 | 0,10 | 0,11 |
Из приведенных данных видно, что до 2073 К окисленность расплава определяет содержание хрома 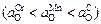 . При более высоких температурах (выше 2073 К) соотношение величин
. При более высоких температурах (выше 2073 К) соотношение величин 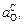
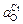 и
и 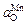 изменяется
изменяется  , и окисленность расплава определяется содержанием углерода, т.е. становится возможным обезуглероживание в форме восстановления оксидов хрома и марганца растворенным углеродом. При низких концентрациях углерода скорость этой реакции мала и окисленность расплава зачастую фактически определяется содержанием хрома.
, и окисленность расплава определяется содержанием углерода, т.е. становится возможным обезуглероживание в форме восстановления оксидов хрома и марганца растворенным углеродом. При низких концентрациях углерода скорость этой реакции мала и окисленность расплава зачастую фактически определяется содержанием хрома.
6. Газы в сталях и шлаках
53. Определение растворимости
азота в расплавах с помощью
параметров взаимодействия
Задача. Рассчитать с помощью параметров взаимодействия растворимость азота в расплаве коррозионно-стойкой стали типа Х18Н9 при 1600°С и 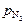 =1,01·105 Па (1 атм).
=1,01·105 Па (1 атм).
Исходные данные. 1. Состав стали: 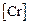 = 18 %;
= 18 %; 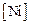 = 9 %;
= 9 %; 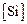 = 0,5 %;
= 0,5 %; 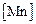 = 1,5 %. 2. Растворимость азота в железе при
= 1,5 %. 2. Растворимость азота в железе при 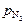 =
=
= 1 атм и 1600 °С равна 0,045 %. 3. 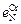 = –0,047;
= –0,047; 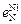 = 0,0063;
= 0,0063; 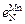 = –0,02;
= –0,02; 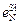 = 0,047;
= 0,047; 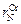 =0,00032;
=0,00032; 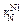 =0,00007;
=0,00007; 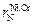 = –0,00008 (или взять из табл. П3).
= –0,00008 (или взять из табл. П3).
Теория. Рассмотрим два расплава: железо и сталь типа Х18Н9, находящиеся в равновесии с газовой фазой при давлении 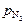 = 1 атм и температуре1600 °С. Очевидно, что активности азота в этих расплавах будут равны:
= 1 атм и температуре1600 °С. Очевидно, что активности азота в этих расплавах будут равны:
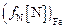 =
= 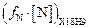 .
.
Стандартным состоянием при этом служит разбавленный 1 %-ный раствор азота в железе. Учитывая, что 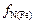 = 1, получаем
= 1, получаем
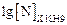 =
= 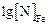 –
– 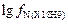 ,
,
где
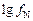 =
= 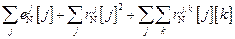 .
.
Решение
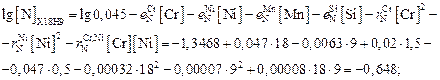
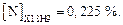
54. Вычисление растворимости азота
в нержавеющей стали с помощью уравнения Чипмана – Корригана
Задача. Вычислить растворимость азота в жидкой стали типа Х18Н9 при 1700 °С и 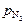 = 0,101 МПа (1 атм), воспользовавшись уравнением Чипмана – Корригана1.
= 0,101 МПа (1 атм), воспользовавшись уравнением Чипмана – Корригана1.








