3. Поверхностные явления в металлургических процессах
32. Расчет поверхностного натяжения расплава
по уравнению Шишковского
Задача. Используя уравнение Шишковского, рассчитать поверхностное натяжение и определить адсорбцию серы в расплаве Fe–S (0,1 %) при 1873 К.
Исходные данные. 1. Поверхностное натяжение чистого железа при 1873 К sFe = 1800 мДж/м2; для железа, содержащего 0,008 % S, sспл = 1580 мДж/м2. 2. Размер площади, занимаемой молекулой FeS на поверхности (s), равен 14×10-20 м2.
Теория. Уравнение Шишковского для расчета поверхностного натяжения разбавленных растворов (s), полученное автором в 1908 г. эмпирически, имеет вид [3]
s = s0 - zRT ln(1 + bc), (3.1)
где s0 - поверхностное натяжение растворителя; с - концентрация растворенного вещества; z и b - константы; R - универсальная газовая постоянная; Т - абсолютная температура.
В уравнении (3.1) вместо концентрации лучше подставить активность растворенного вещества (если есть данные). Адсорбция компонента определяется уравнением Лангмюра:
Г = (zbc)/(1 + bc), (3.2)
где z - число мест, которое адсорбент представляет адсорбату; b - отношение констант скоростей прямого и обратного процессов (адсорбция–десорбция).
Решение. Для вычисления sспл по уравнению (3.1) должны быть известны величины z и b.
Для определения z пользуемся формулой
z = 1/s×NA (NA - число Авогадро),
отсюда
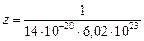 = 1,19×105 моль/м2 .
= 1,19×105 моль/м2 .
Величину b определим из уравнения (3.1) для с = 0,008 %:
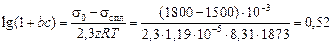 ,
,
тогда 1 + bс = 3,31 и b = (3,31 - 1)/0,008 = 289.
Величина sспл , определяемая по уравнению (3.1), равна sспл = = 1800 - 103×1,19×10-5 - 8,31×1873×2,3 lg (1 + 289×0,1) = 1800 - 628 » » 1170 мДж/м2. Экспериментальное значение sспл этого расплава составляет 1200 мДж/м2.
Уравнение Шишковского хорошо описывает поверхностное натяжение металлургических расплавов при малых концентрациях примеси.
Для расчета поверхностного натяжения жидкого железа, содержащего серу и кислород, можно использовать также следующую изотерму [25], являющуюся разновидностью уравнения Шишковского:
s = sFe - 2000 lg [1 + (Fi - 1)х i ], (3.3)
где х i - мольная доля О или S; Fi - параметр, характеризующий капиллярную активность растворенного вещества, равный для серы 500, а для кислорода - 1000 [25].
Для малых концентраций серы уравнение (3.3) дает завышенные значения s. Например, для 0,1 % [S] имеем
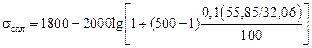 =
=
= 1800 - 560 = 1240 мДж/м2 ,
что близко к экспериментальному значению sспл = 1200 мДж/м2.
Используя уравнение Лангмюра (3.2), определяем адсорбцию серы на поверхности железа:
ГS = 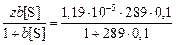 = 1,15×10-5 моль/м2 .
= 1,15×10-5 моль/м2 .
Примечание. Для оценки s расплавов Fe–О также можно рекомендовать уравнение (3.1). Расчеты по уравнению (3.3) при [О] £ 0,1 % дают значения s, превышающие полученные экспериментально. Например, для железа, содержащего 0,1 % [О],
sспл = 1800 - 1000 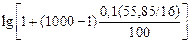 = 1800 - 650 =
= 1800 - 650 =
= 1150 мДж/м2 ,
в то время как экспериментальное значение s такого расплава равно 950 мДж/м2 [2].
33. Расчет поверхностного натяжения расплава по изотерме Жуховицкого для идеальных растворов
Задача. По уравнению Жуховицкого для идеальных растворов рассчитать поверхностное натяжение сплава Fe–Мn при 1823 К, если концентрация марганца равна 20 %. Сравнить его со значением, полученным по уравнению изотермы поверхностного натяжения для регулярных растворов.
Исходные данные. 1. Поверхностное натяжение чистого железа sFe = 1820 мДж/м2 , марганца sMn = 1010 мДж/м2 . 2. Плотность жидкого железа rFe = 7,15×103 кг/м3 , марганца rMn = 6,75×103 кг/м3 .
Теория. Уравнение Жуховицкого для поверхностного натяжения идеального раствора имеет вид [25]:
s = si + (1/wi ) RT 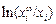 , (3.4)
, (3.4)
где si - поверхностное натяжение чистого i-го компонента; wi - поверхностная мольная площадь этого компонента; х i и 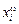 - объемная и поверхностная концентрация i-го компонента раствора. Для двухкомпонентного раствора имеем
- объемная и поверхностная концентрация i-го компонента раствора. Для двухкомпонентного раствора имеем
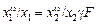 , (3.5)
, (3.5)
где F = ехр[(s2 - s1)/RT ]w1 ; g - коэффициент вытеснения, равный
g = w1 /w2 .
Если g = 1, то
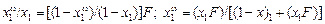 . (3.6)
. (3.6)
Последнее уравнение связывает состав поверхностного раствора с составом раствора в объемной фазе.
С учетом формул (3.6) выражение (3.4) для двухкомпонентного раствора имеет вид
s = s2 - (1/w1)RT ln(1 - x1 + x1F ). (3.7)
Уравнение (3.7), выведенное А.А. Жуховицким в 1944 г., хорошо описывает поверхностное натяжение совершенных растворов в широком интервале концентраций компонентов.
Решение. Для расчета sспл по уравнению (3.7) поверхностные мольные площади железа (wFe) и марганца (wMn) определим из мольных объемов этих компонентов (Vm), приняв, что коэффициент упаковки равен 1:
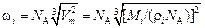 , (3.8)
, (3.8)
где Mi - атомная масса; ri - плотность; NA - число Авогадро.
Тогда
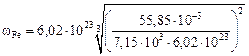 = 3,3×104 м2; (3.9)
= 3,3×104 м2; (3.9)
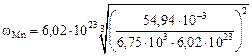 = 3,4×104 м2. (3.10)
= 3,4×104 м2. (3.10)
Поскольку wFe » wMn и g = 1, то и для расчета sспл можем воспользоваться уравнением (3.7). При этом
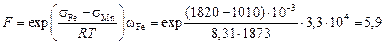 .
.
Для расплава 20 % Mn–Fe имеем
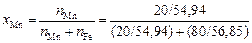 = 0,203
= 0,203
и окончательно получаем sспл = 1820 - (103/3,3×104 )×8,31×1873×2,3×(1 -
- 0,203 + 5,9×0,203) » 1500 мДж/м2, что не очень сильно отличается от экспериментального значения - 1420 мДж/м2 [25].
Для регулярных растворов уравнение Жуховицкого имеет вид
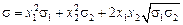 . (3.11)
. (3.11)
Тогда sспл = (0,203)2 ×1010 + (0,797)2 ×1820 + 2×0,203×0,797×1820×1010 » » 1640 мДж/м2 . Видно, что уравнение (3.11) дает явно завышенные значения s данного расплава.
Примечание. Для вычисления поверхностного натяжения бинарных растворов на основе железа в работе [25] С.И. Попель рекомендует обобщенное уравнение:
s = sFe - 2000 lg [1 + (Fi - 1)xi ], (3.12)
где Fi - параметр, характеризующий капиллярную активность примеси. Табличные значения теоретических и экспериментальных Fi приведены в работе [25] (см. задачу 37).
Для сплава 30 % Fe–20 % Mn расчет по уравнению (3.12) дает следующие значения:
sспл = 1820 - 2000 lg [1 + (5 - 1)×0,203] » 1300 мДж/м2 .
Таким образом, по уравнению (3.12) в отличие от выражений (3.7) и (3.11) получаются несколько заниженные значения sспл .
34. Расчет поверхностного натяжения сплава
по изотерме Жуховицкого для реальных растворов
Задача. Вычислить поверхностное натяжение железа, содержащего 0,2 % S при 1823 К, по уравнению Жуховицкого для реальных растворов.
Исходные данные. 1. Поверхностное натяжение чистого железа sFe = 1860 мДж/м2 , сульфида железа sFeS = 500 мДж/м2. 2. Плотность жидкого железа rFe = 7,15×103 кг/м3. 3. Концентрационная зависимость активностей Fe и FeS в сплавах Fe–S (по данным [26]) представлена в таблице.
| xFe | aFe | xFeS | aFeS |
| 0 | 0 | 1,0 | 1,0 |
| 0,10 | 0,39 | 0,90 | 0,90 |
| 0,20 | 0,099 | 0,80 | 0,840 |
| 0,30 | 0,15 | 0,70 | 0,742 |
| 0,40 | 0,222 | 0,60 | 0,660 |
| 0,50 | 0,315 | 0,50 | 0,610 |
| 0,60 | 0,418 | 0,40 | 0,560 |
| 0,70 | 0,566 | 0,30 | 0,528 |
| 0,80 | 0,726 | 0,20 | 0,480 |
| 0,90 | 0,87 | 0,10 | 0,365 |
| 0,95 | 0,945 | 0,05 | 0,235 |
| 0,99 | 0,990 | 0,01 | 0,061 |
| 1,00 | 1,000 | 0 | 0 |
Теория. В общем случае изотерма поверхностного натяжения реального раствора описывается в теории Жуховицкого следующим уравнением:
s = si + (l/wi )RT 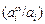 , (3.13)
, (3.13)
где s - поверхностное натяжение сплава; si - поверхностное натяжение чистого i-го компонента; ai и 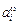 - активности i-го компонента в объеме и на поверхности соответственно (для соответствующих стандартных состояний см. [74, с. 305]); wi - мольная поверхностная площадь i-го компонента.
- активности i-го компонента в объеме и на поверхности соответственно (для соответствующих стандартных состояний см. [74, с. 305]); wi - мольная поверхностная площадь i-го компонента.
Допускается, что термодинамические функции (в частности, активности) компонентов поверхностного и объемного растворов с изменением состава изменяются одинаково. В этом случае поверхностное натяжение сплава (sспл) любой концентрации можно определить, зная лишь активности компонентов в объемном растворе.
Запишем уравнение (3.13) для каждого компонента:
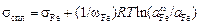 , (3.14)
, (3.14)
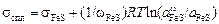 . (3.15)
. (3.15)
Вычитая выражение (3.15) из формулы (3.14), получаем
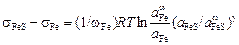 , (3.16)
, (3.16)
где g - коэффициент вытеснения, равный g = wFe /wFeS .
Отсюда
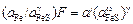 , (3.17)
, (3.17)
F = ехр[(sFeS - sFe)/RT ]wFe . (3.18)
Соотношение (3.17) устанавливает связь между активностями компонентов в объеме и поверхностном слое (при указанном выборе стандартных состояний).
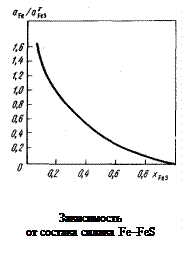
Решение. Значения sспл удобно вычислять графическим способом. По концентрационным зависимостям активностей Fе и FeS [26]
(см. с. 99) строим график зависимости 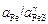 от состава расплава (рисунок). Значение g можно рассчитать по известным размерам площадок, занимаемых молекулами железа и сульфида железа в поверхностном слое. По экспериментальным данным величина wFeS/NA колеблется в пределах (12-14,5)×10-20 м2 [25]. Значение wFe /NA можно определить, зная rFe, по формуле
от состава расплава (рисунок). Значение g можно рассчитать по известным размерам площадок, занимаемых молекулами железа и сульфида железа в поверхностном слое. По экспериментальным данным величина wFeS/NA колеблется в пределах (12-14,5)×10-20 м2 [25]. Значение wFe /NA можно определить, зная rFe, по формуле
wFe /NA = [MFe /(rFe NA)]2/3, (3.19)
 где MFe - атомная масса железа.
где MFe - атомная масса железа.
Подставив соответствующие значения в уравнение (3.19), получим wFe /NA = = 5,6×1023×10-20 ; тогда wFe = 5,6×6,02×10-20 = = 3,4×104 м2/моль, а g = (5,6×10-20)/(14×10-20) »
» 0,4. Теперь найдем величину F в уравнении (3.18):
|
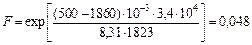 .
.
Пересчитаем массовое содержание серы (%) на мольное FeS (xFeS) и по, данным [26] найдем значения активностей Fe и FeS в сплаве Fe–S: xFeS = = 0,0035, aFeS = 0,0245 и aFe » 1. Исходя из предположения, что активности компонентов объемного и поверхностного растворов изменяются при изменении состава одинаково, умножаем 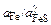 на 0,048 и находим на графике точку с ординатой, равной
на 0,048 и находим на графике точку с ординатой, равной
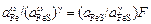 = 4,41×0,048 = 0,212.
= 4,41×0,048 = 0,212.
Абсцисса этой точки соответствует мольной доле FeS в поверхностном слое сплава 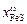 = 0,670; тогда
= 0,670; тогда 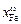 = 1 - 0,670 = 0,330. Указанной концентрации xFe = 0,33 соответствует aFe = 0,177 (см. с. 99).
= 1 - 0,670 = 0,330. Указанной концентрации xFe = 0,33 соответствует aFe = 0,177 (см. с. 99).
Окончательно по формуле (3.14) имеем
sспл = 1860 + 1054 lg(0,177/1) = 1070 мДж/м2.
Значение s для этого сплава, рассчитанное по уравнению Шишковского, составляет 1130 мДж/м2, что близко к рассчитанному по формуле (3.13). Экспериментально полученная величина sспл = 1100 мДж/м2 [25].
35. Расчет поверхностного натяжения сплава
и поверхностных концентраций компонентов
по уравнению Попеля – Павлова
Задача. Рассчитать поверхностное натяжение сплавов Fe–Мn по уравнению Попеля – Павлова при 1823 К. Сравнить полученные значения с рассчитанными по уравнению Жуховицкого. Определить поверхностную концентрацию и адсорбцию марганца в этих сплавах.
Исходные данные. 1. Поверхностное натяжение железа sFe =
= 1850 мДж/м2, марганца sMn = 1060 мДж/м2. 2. Плотность жидкого железа rFe = 7,15×103 кг/м3, марганца rMn = 6,75×103 кг/м3.
Теория. Уравнение Попеля – Павлова [25] в отличие от уравнений Жуховицкого и Шишковского, в которых для расчета s расплавов необходимо использовать лишь характеристики чистых компонентов, требует знания большего числа параметров. Это уравнение имеет вид
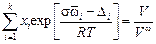 , (3.20)
, (3.20)
где 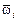 - парциальная поверхностная мольная площадка i-го компонента; Di - работа выхода моля i-го компонента в поверхностный слой, [Di =
- парциальная поверхностная мольная площадка i-го компонента; Di - работа выхода моля i-го компонента в поверхностный слой, [Di = 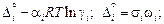 ai - коэффициент, характеризующий долю недостающих связей частицы в поверхностном слое и равный ~ 1/4 для Fe, Ni, Mn, Cr, V и Ti и ~ 1/6 для Si, P, Н]; V и Vw - мольные объемы раствора в объеме и в поверхностном слое расплава соответственно.
ai - коэффициент, характеризующий долю недостающих связей частицы в поверхностном слое и равный ~ 1/4 для Fe, Ni, Mn, Cr, V и Ti и ~ 1/6 для Si, P, Н]; V и Vw - мольные объемы раствора в объеме и в поверхностном слое расплава соответственно.
Решение. Для двухкомпонентного раствора уравнение (3.20) имеет вид
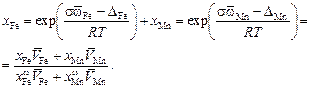 (3.21)
(3.21)
Вычислим последовательно 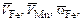 DFe, DMn и другие необходимые величины.
DFe, DMn и другие необходимые величины.
1. Поскольку железо и марганец образуют раствор, близкий к совершенному, то DV = 0 и парциальные мольные объемы компонентов равны мольным объемам чистых компонентов, т.е.
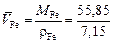 = 7,81 см3/моль;
= 7,81 см3/моль;
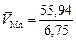 = 8,29 см3/моль.
= 8,29 см3/моль.
2. Парциальная мольная площадь компонента wi равна 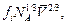 где fi - коэффициент упаковки, в первом приближении равный 1. Тогда
где fi - коэффициент упаковки, в первом приближении равный 1. Тогда 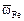 = (6,02×1023)1/3 (7,81)2/3 = 3,32×108 см2 = 3,32×104 м2×моль, а
= (6,02×1023)1/3 (7,81)2/3 = 3,32×108 см2 = 3,32×104 м2×моль, а 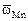 =
=
= (6,021023)1/3×(8,29)2/3 = 3,45×108 см2 = 3,45×104 м2×моль.
3. Поскольку раствор близок к совершенному, то Di » 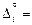 siwi и
siwi и
DFe = 1850×3,32×104 = 6,14×107 мДж, а DMn = 1060×3,45×104 = 3,68×107 мДж.
4. 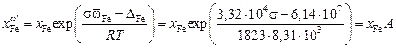 ;
;
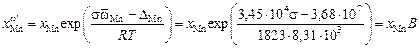 , где А и В – выражения в скобках.
, где А и В – выражения в скобках.
Концентрации компонентов в поверхностном слое равны соответственно
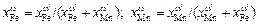 . (3.22)
. (3.22)
Подставив выражение (3.22) в формулу (3.21), получим
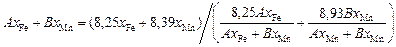 .
.
Окончательно расчетная формула для вычислений s (мДж/м2) имеет следующий вид:
7,81хFe + 8,29хMn = 0,14хFe exp(3,32s/1515) + 0,73хMn exp(3,45s/1515). (3.23)
Например, для 20 % Мn расчет по уравнению (3.23) дает а =
= 1520 мДж/м2. Полученные значения s для сплавов Fе–Мn во всем интервале концентраций приведены на рисунке (кривая 1). Значения s, вычисленные по уравнению Жуховицкого (см. задачу 33), также представлены на рисунке (кривая 2).
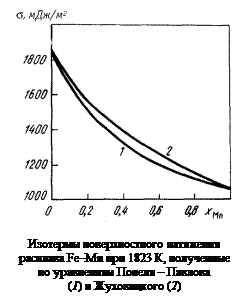 Для расплавов Fе–Мn, близких к совершенным, оба метода дают близкие результаты. Для многих реальных металлургических систем расчеты s по уравнению (3.20) затруднены отсутствием соответствующих данных в литературе. Применяемые упрощения снижают точность расчетов. Вместе с тем уравнение Попеля–Павлова позволяет описывать особые точки на изотермах поверхостного натяжения.
Для расплавов Fе–Мn, близких к совершенным, оба метода дают близкие результаты. Для многих реальных металлургических систем расчеты s по уравнению (3.20) затруднены отсутствием соответствующих данных в литературе. Применяемые упрощения снижают точность расчетов. Вместе с тем уравнение Попеля–Павлова позволяет описывать особые точки на изотермах поверхостного натяжения.
Теперь вычислим поверхностную концентрацию и адсорбцию марганца в сплаве с железом при 10 % Мn. Согласно уравнению (3.22)
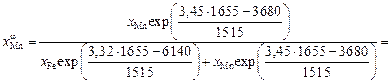
= 0,394 или [Мn]w = 39 %.
По уравнению Жуховицкого (3.7) (задача 33) величина 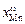 для этого же расплава равна 0,355. Величина адсорбции компонента связана с его поверхностной и объемными концентрациями следующим уравнением:
для этого же расплава равна 0,355. Величина адсорбции компонента связана с его поверхностной и объемными концентрациями следующим уравнением:
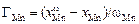 . (3.24)
. (3.24)
Отсюда
GMn = (0,394 - 0,102)/(3,45×108) = 8,46×10-10 моль/см2 =
= 8,46×10-6 моль/м2.
Значение GMn характеризует превышение концентрации марганца в поверхностном слое над его объемной концентрацией.
36. Адсорбция компонентов в расплавах
Задача. По экспериментальным данным о зависимости поверхностного натяжения жидкого железа от содержания серы определить адсорбцию серы.
Исходные данные. Концентрационная зависимость поверхностного натяжения расплавов Fe–S при 1873 К:
| [ S ], % | 0 | 0,03 | 0,09 | 0,14 | 0,17 | 0,22 | 0,33 |
| s, мДж/м2 | 1790 | 1410 | 1210 | 1155 | 1090 | 1045 | 980 |
Теория. Уравнение адсорбции по Гиббсу для двухкомпонентного раствора имеет вид
Gi = -(ai /RT )(ds/dai ) , (3.25)
где ai - активность растворенного вещества (или концентрация для разбавленных растворов). Величину Gi удобно вычислять графически. С этой целью в ряде точек на кривой зависимости s от ai ([i], %) необходимо определить тангенсы угла наклона касательных, равные 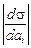 .
.
Решение. По экспериментальным данным строим изотерму поверхностного натяжения сплавов Fe–S (рисунок). Находим тангенсы угла наклона касательных в точках 1 (0,05 % [S]), 2 (0,10 % [S]), 3 (0,15 % [S]) и 4 (0,25 % [S]): tg j1 = 3700; tg j2 = 2100; tg j3 = 1400; tg j4 = 620. Адсорбцию в каждой точке определяем по формуле
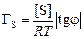 , (3.26)
, (3.26)
тогда
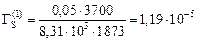 моль/м2.
моль/м2.
В точках 2, 3 и 4 GS составляет соответственно 1,28×10-5, 1,35×10-5 и 0,99×10-5 моль/м2. Как видно из рисунка (кривая 2), концентрационная зависимость адсорбции имеет максимум в точке [S]*.
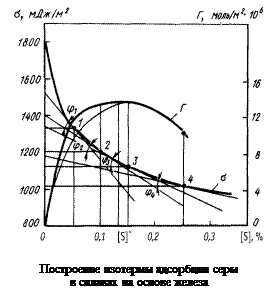 При данной концентрации серы поверхностный слой сплава насыщен этим компонентом, и дальнейшее увеличение [S] приводит к снижению GS в соответствии с уравнением
При данной концентрации серы поверхностный слой сплава насыщен этим компонентом, и дальнейшее увеличение [S] приводит к снижению GS в соответствии с уравнением
GS » ([S]w - [S])/wS , (3.27)
где [S]w - поверхностная концентрация серы; wS - поверхностная мольная площадка этого компонента.
Примечание. Более точное уравнение адсорбции Адама – Гугенгейма, в котором для двухкомпонентного раствора G1 + G2 = 0 в отличие от уравнения (3.25), где принимается, что Gi = 0, имеет вид [25]:
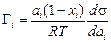 , (3.28)
, (3.28)
т.е. отличается множителем (1 - xi). Уравнение (3.28) для концентрированных растворов дает результаты, существенно отличные от уравнения (3.25). Однако для разбавленных растворов, где мольная доля примеси xi ® 0, выражение (3.28) переходит в формулу (3.25). Например, для 0,25 % [S] величина (1 - xS ) = 0,9865 » 1.
37. Расчет поверхностного натяжения стали
Задача. Рассчитать поверхностное натяжение коррозионно-стойкой стали при 1873 К. Определить поверхностные концентрации основных легирующих элементов.
Исходные данные. 1. Состав стали в ковше: 0,15 % С; 1,16 % Мn; 0,54 % Si, 0,014 % S; 17,68 % Сr, 0,0075 % О; 8,87 % Ni. 2 . sFe =
= 1800 мДж/м2.
Теория. Для расчета поверхностного натяжения сталей можно рекомендовать следующую обобщенную формулу [25]:
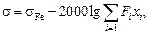 (3.29)
(3.29)
где Fi - параметр, характеризующий капиллярную активность легирующей добавки. Его значения для 1873 К [25]:
| Элемент | Fе | С | Si | Mn | Ni | Cr | Ti | V | Мо | Р | S | О | N |
| Fi | 1 | 2,0 | 2,2 | 5,0 | 1,4 | 2,5 | 0,12 | 0,6 | 0,45 | 1,5 | 500 | 1000 | 150 |
Приближенные значения Fi для других температур Т можно получить по уравнению
Fi(T ) = [Fi(1873)]1873/T. (3.30)
Поверхностную концентрацию любого компонента сплава 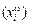 рассчитывают по формуле
рассчитывают по формуле
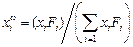 . (3.31)
. (3.31)
Решение. Поверхностное натяжение стали 12Х18Н9 по формуле (3.29)
s = 1800 - 2000lg(FFexFe + FCxC + FSixSi + FMnxMn + FCrxCr + FNixNi +
+ FОxО + FSxS );
s = 1800 – 2000 lg(1×0,695 + 2×0,007 + 2,2×0,0107 + 5×0,012 + 2,5×0,184 +
+ 1,4×0,082 + 1000×0,0003 + 500×0,0003) = 1800 – 540 = 1260 мДж/м2.
Экспериментальное значение s для этой стали составляет 1200 мДж/м2. Поверхностные концентрации компонентов стали определяем по уравнению (3.31):
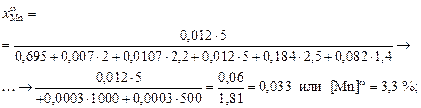
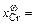 0,254; [Cr]w = 23,6 %;
0,254; [Cr]w = 23,6 %; 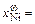 0,0635, [Ni]w = 6,8 %;
0,0635, [Ni]w = 6,8 %;
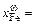 0,345, [Fe]w = 34,5 %;
0,345, [Fe]w = 34,5 %; 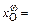 0,166, [О]w = 4,7 %;
0,166, [О]w = 4,7 %;
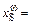 0,083, [S]w = 4,7 %.
0,083, [S]w = 4,7 %.
Из расчета видно, что поверхностные концентрации легирующих элементов значительно отличаются от их содержания в объеме расплава. Это следует учитывать при рассмотрении металлургических реакций, протекающих на поверхностях раздела фаз.
Примечания. 1. Поверхностное натяжение многокомпонентных расплавов можно оценить также по формуле
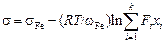 , (3.32)
, (3.32)
где wFe - поверхностная мольная площадь железа.
Вместе с тем анализ большого числа экспериментальных и расчетных данных s позволяет заключить, что если в эту формулу подставить wFe = 3,4×104 м2, то значения поверхностного натяжения для сталей получаются явно завышенными. С.И. Попель для оценки s стали и чугуна предлагает использовать следующее уравнение [25] :
s = sFe - 2000 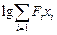 - 1000 [lg(1 + FOxO ) + lg(l + FSxS )] , (3.33)
- 1000 [lg(1 + FOxO ) + lg(l + FSxS )] , (3.33)
в котором для расплавов всех компонентов, кроме серы и кислорода, wFe принимается равным 1,74×104 м2, а в случае серы и кислорода wFe = = 3,48×104 м2.
Однако, как уже было показано в задаче 32, для низких концентраций кислорода и серы (менее 0,1 %) использование коэффициента 1000 перед знаком логарифма также дает завышенные значения s. Например, в нашем случае расчет по уравнению (3.33) дает s = = 1360 мДж/м2.
2. Если не известно табличное значение F i в уравнениях (3.29) или (3.32), то эту величину можно оценить по формуле
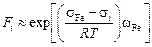 .
.
38. Работы адгезии и когезии, коэффициент растекания
Задача. Рассчитать работу адгезии и когезии, а также коэффициент растекания в системе известково-глиноземистый шлак–сталь ШХ15 при 1823 К.
Исходные данные. 1. Состав шлака: 55 % СаО; 45 % Аl2О3 . 2. Поверхностное натяжение стали ШХ15 sм = 1590 мДж/м2; шлака sш = = 600 мДж/м2. 3. Краевой угол смачивания стали шлаком q = 15°.
Теория. Для того чтобы разделить металл и шлак по поверхности их соприкосновения площадью 1 м2, необходимо затратить энергию, равную работе адгезии Wa . При этом исчезает поверхность раздела металл–шлак и образуются две новые поверхности: металл–газ и шлак–газ. Тогда
Wa = sм + sш - sм–ш . (3.34)
Величину sм–ш можно вычислить по следующей формуле [25]:
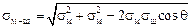 . (3.35)
. (3.35)
Характеристикой растекания одной жидкости по поверхности другой (или по твердой подложке) является коэффициент растекания Харкинса S. По определению
S = sм - sш - sм–ш . (3.36)
Если S > 0, то шлак растекается по поверхности металла, если S < 0, то шлак собирается в линзу. Коэффициент растекания можно выразить через величины работы адгезии на границе металл–шлак и работы когезии Wк, равной работе разрыва столба шлака с поперечным сечением 1 м2, т.е.
Wк = 2sш . (3.37)
Тогда формула (3.36) имеет вид
S = Wа - Wк . (3.38)
Если Wа > Wк, то S > 0, если Wа < Wк, то S < 0.
Решение. Межфазное натяжение на границе известково-глиноземистый шлак–сталь ШХ15 определяем по уравнению (3.35) :
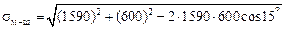 = 1030 мДж/м2.
= 1030 мДж/м2.
Работа когезии для известково-глиноземистого шлака и работа адгезии данного шлака к стали ШХ15 равны соответственно Wк = 2×600 =
= 1200 мДж/м2; Wа = 1590 + 600 - 1025 = 1170 мДж/м2. Очевидно, что чем больше величина Wа , тем труднее отделить шлак от металла. Рассчитаем коэффициент растекания Харкинса для данной системы: S = 1170 - 1200 = -30 мДж/м2. Отрицательное значение S показывает, что известково-глиноземистый шлак при 1823 К неполностью растекается по поверхности стали ШХ15.
Примечания. 1. Если неизвестно значение q, то sм–ш можно приближенно определить по правилу Антонова:
sм–ш » sм - sш . (3.39)
Для данной системы расчет по этой формуле дает sм–ш = 990 мДж/м2.
2. Величины sм–ш и Wа оказывают решающее влияние на процессы образования и разделения шлакометаллической эмульсии, а также рафинирование стали при шлаковой обработке.
Например, в случае перехода неметаллического включения из металла в шлак должно выполняться следующее неравенство:
sм–в > sш–в - sм–ш , (3.40)
sм–в + sм + sш > Wа(м–ш) - sш–в . (3.41)
При обработке известково-глиноземистым шлаком стали ШХ15 в ковше для случая рафинирования металла от твердых включений Аl2O3 по формуле Неймана sм–в = sв - sм cosq = 900 - 1590×cos 140° =
= 2120 мДж/м2, а sш–в 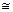 100 мДж/м2 [25]. Неравенство (3.41) выполняется: 2120 + 1590 + 610 > 1200 + 100, т.е. в этом случае из металла достаточно эффективно удаляются включения глинозема.
100 мДж/м2 [25]. Неравенство (3.41) выполняется: 2120 + 1590 + 610 > 1200 + 100, т.е. в этом случае из металла достаточно эффективно удаляются включения глинозема.
4. Кинетика металлургических реакций
39. Кинетические характеристики перехода серы из металла в шлак
Задача. По экспериментальным данным о десульфурации металла определить коэффициент массопереноса серы в шлаке при обработке металла «белым» шлаком в дуговой печи и при выпуске плавки в ковш. Определить время, в течение которого концентрация серы в шлаке в этих условиях достигает 95 % от равновесной.
Исходные данные [27]. При выплавке электротехнической стали в 100-тонной дуговой печи концентрация серы в металле снизилась за 20 мин обработки белым шлаком с 0,028 до 0,022 %. После легирования металла кремнием (на 3 %) концентрация серы уменьшилась до 0,015 %, а при выпуске (в течение 3 мин) снизилась до 0,005 %. Количество шлака составляло при этом 6 % от массы металла.
Равновесный коэффициент распределения серы между белым шлаком и металлом, содержащим ~3 % Si, можно принять равным 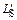 =
=
= (S)/[S] = 150 [27]. Начальную концентрацию серы в шлаке можно принять равной нулю.
Теория. В условии задачи подразумевается, что лимитирующим звеном процесса десульфурации в печи и при выпуске является массоперенос в шлаке, иначе определить характеристики массопереноса по данным о десульфурации невозможно.
Скорость перехода серы в шлак при таком лимитирующем звене описывается уравнением
d(S)/dt = b[(S)пов - (S)], (4.1)
где b - коэффициент массопереноса серы в шлаке; (S)пов - поверхностная концентрация серы в шлаке на границе с металлом; (S) - концентрация серы в объеме шлака.
Величину (S)пов можно считать равновесной с металлом (с текущим значением [S]). Для определения (S)пов вычисляют вначале коэффициент распределения LS , не зависящий от состава металла (поскольку [Si] - переменная величина).
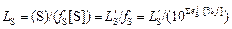 . (4.2)
. (4.2)
По известной величине LS получим
(S)пoв = LS fS [S] . (4.3)
Текущее значение [S] можно определить из балансового соотношения
[S]нaч - [S] = [(S) - (S)нaч ](mш/mм ).
В рассматриваемой задаче (S)нaч = 0. Следовательно,
[S] = [S]нaч - (S)(mш/mм ). (4.4)
Подставив выражения (4.3) и (4.4) в формулу (4.1), получим дифференциальное уравнение
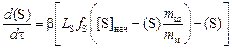 . (4.5)
. (4.5)
Разделив переменные и проинтегрировав (4.5), получим
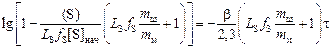 . (4.6)
. (4.6)
Подставив в выражение (4.6) значение t и соответствующую величину (S), найденную из уравнения (4.4), можно определить коэффициент массопереноса b. Далее, подставив в выражение (4.6) значение b и (S)0,95 = 0,95 (S)равн , соответствующую 95 %-ному приближению к равновесию, можно найти t0,95 - время достижения этого состояния.
Чтобы определить (S)равн , необходимо решить систему, состоящую из равновесного уравнения (4.1) и балансового уравнения (4.4). Решение имеет вид
(S)paвн = [S]нач /{(mш /mм) + [l/(LS fS)]}; (4.7)
[S]paвн = [S]нач / [LS fS(mш /mм) + l]. (4.8)
Решение. Для расплава, не легированного кремнием, примем fS = 1. После легирования: lg fS = 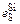 [% Si] = 0,063×3 = 0,189; fS = 1,545. Подставив значение fS в уравнение (4.2), получим
[% Si] = 0,063×3 = 0,189; fS = 1,545. Подставив значение fS в уравнение (4.2), получим
LS = 150/1,545 = 97.
Из уравнения (4.4) определим: после 20-минутной обработки шлаком в печи
(S) = (1/0,06)×(0,028 - 0,022) = 0,1 %;
после выпуска
(S) = (1/0,06)×(0,028 - 0,005) = 0,383 %.
Из уравнения (4.6) получим:
для десульфурации в печи
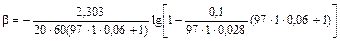 =
=
= 0,35×10-4 с-1,
для десульфурации при выпуске
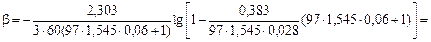 = 9,56×104 с-1.
= 9,56×104 с-1.
Из уравнений (4.7) и (4.8) получим:
для десульфурации нелегированного металла
(S)равн = 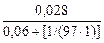 = 0,398 %;
= 0,398 %;
[S]равн = 0,028/(97×1×0,06 + 1) = 0,0041 %;
для десульфурации легированного металла:
(S)равн = 0,028/{0,06 + [1/(97×1,545)]} = 0,420 %.
[S]равн = 0,028/{97×1,545 - 0,06 + l} = 0,0028 %.
Из уравнения (4.6):
для десульфурации в печи
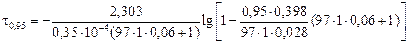 = = 12500 с = 3,47 ч;
= = 12500 с = 3,47 ч;
для десульфурации при выпуске
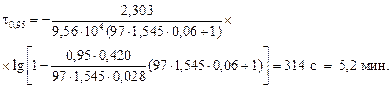
Примечание. Иногда для анализа кинетики десульфурации применяют выражение
lg{[(S)pавн - (S)]/(S)pавн} = -(b/2,303)t ,
где (S)pавн = LS fS [S] .
Это выражение является результатом интегрирования уравнения (4.1) при условии [S] = const. Очевидно, что его можно использовать только при соблюдении этого условия, например, при очень малых значениях mш /тм или LS .
40. Удаление водорода из жидкой стали
при обезуглероживании
Задача. Определить скорость удаления водорода d [H]/dt из ванны дуговой электропечи при заданной скорости обезуглероживания d[C]/dt, а также конечную концентрацию водорода [Н]к при окислении заданного количества углерода D[С].
Исходные данные. 1. Вместимость дуговой электропечи g = 100 т. 2. Скорость обезуглероживания d[C]/dt = 1 %/ч. 3. Исходная концентрация водорода [Н]исх = 9×10-4 %. 4. Количество окислившегося углерода D[С] = 0,3 %.
Теория. Водород в процессе кипения ванны в основном удаляется пузырями оксида углерода. При количественных расчетах в настоящей задаче предполагают наличие равновесия между растворенным в стали водородом и его парциальным давлением в пузыре:
Н2 = 2[Н]; KH1873 = [% H]2/pH2 = 0,73×10-5 . (4.9)
Другими словами, вычисляются максимально возможная скорость удаления водорода и его минимально возможная концентрация (без учета кинетических затруднений).
Если в процессе обезуглероживания образуется пузырь СО объемом dV, в котором парциальное давление водорода равно pH2 , то концентрация водорода в металле уменьшается на d[H] (%). Уравнение материального баланса для этого случая имеет вид
dVCO pH2 /22,4 = -(1000 g×d [H]/2×100) , (4.10)
где 22,4 - объем (м3) 1 кг-моля газа при нормальных условиях, а произведение pH2 dVCO - объем водорода в пузыре dV.
Таким образом, левая часть уравнения (4.10) соответствует мольной доле водорода в газовой фазе (СО, кг/моль), а правая часть характеризует количество водорода (кг/моль), выделившееся из жидкого металла. Применительно к углероду балансовое уравнение имеет вид
pCO dVCO = -(1000 gd [С]/12×100) . (4.11)
Разделив (4.10) на (4.11), получим
-d[H]/-d[C] = (2/12)(pH2/рCO). (4.12)
Приняв, что PH2 << PСО и что при открытой плавке PСО = 1 атм (на выходе пузырька из металла) и продифференцировав уравнение (4.12) по времени, получим
-d[H]/dt = -(2/12)([Н]2d[С]/KH dt ) . (4.13)
Из уравнения (4.13) видно, что скорость удаления водорода линейно зависит от скорости обезуглероживания и пропорциональна [Н]2.
Вычислим содержание водорода в жидкой стали [% Н] при окислении заданного количества углерода D[С] = [С]н - [С]к . Количество окислившегося углерода D[С] и объем образовавшегося оксида (dVCO) связаны зависимостью
d[C] = [(12×100)/(22,4×1000g)]dVCO . (4.14)
В этом случае уравнение (4.10) с учетом формулы (4.14) имеет вид
-d[C] = -(12/2)КH (d[H]/[H]2) . (4.15)
В результате интегрирования получим
D[С] = (12/2)КH [(1/[Нк) - (1/[Н]н)] ,
откуда
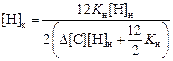 . (4.16)
. (4.16)
Решение. В соответствии с исходными данными по уравнению (4.13) вычисляем максимальную (начальную) скорость удаления водорода
d[H]/dt = (2×81×10-8)/(12×0,73×10-5) = 0,018 %/ч.
Конечную концентрацию водорода вычисляем по уравнению (4.16):
[Н]к = (12×0,73×10-5×9×10-4)/[2(0,3×9×10-4 + (12/2)0,73×10-5)] »
» 1,0×10-4 %.
Средняя скорость удаления водорода за период окисления 0,3 % С равна 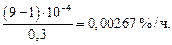
Примечания. 1. Максимальную (начальную) скорость удаления водорода можно также найти следующим образом. По закону Сивертса
pH2 = (0,0009/0,0027)2 = 0,11 атм,
где 0,0027 % - константа Сивертса, равная растворимости водорода в жидком железе при 1873 К и pH2 = 1 атм.
Максимальная скорость удаления водорода составит
d[H]/dt = (1/12)0,11×2 = 0,018 %/ч,
где 1/12 - скорость обезуглероживания (моль/ч), 2 – масса моля водорода. Множитель 106 в уравнении не записан, так как он должен стоять в числителе (для углерода) и в знаменателе (для водорода) .
2. Для азота опытные значения [N]к , как правило, получаются более высокими, чем по формуле (4.16). Это связано с тем, что удаление водорода осуществляется в условиях, более близких к равновесным, чем удаление азота. В последнем случае кинетические затруднения играют большую роль.
41. Лимитирующая стадия абсорбции азота
Задача. По экспериментальным данным о кинетике поглощения азота жидким железом определить лимитирующую стадию процесса. Оценить роль поверхностно-активных веществ (ПАВ).
Исходные данные. Тигель с расплавом жидкого железа обдували азотом при pN2 = 1 атм и 1873 К. В первой плавке (А ) металл раскислили малым количеством алюминия ([% Аl]ост ® 0). Во второй плавке (Б ) добавкой окалины содержание кислорода поддерживали на уровне 0,09 %. Равновесная с pN2 = 1 атм концентрация азота [N] = 0,044 %. Исходная концентрация азота [N]0 = 0,006 %.
В таблице приведены экспериментальные данные по кинетике поглощения азота жидким железом.
| Время, с | Плавки | |
| A; [O] ® 0 | Б; [O] = 0,09 | |
| 0 300 600 900 1200 1500 | 0,006 0,015 0,022 0,024 0,028 0,032 | 0,006 0,011 0,015 0,018 0,020 0,022 |
Теория. Кинетика растворения азота в жидком металле включает три стадии: 1) внешнюю диффузию - массоперенос азота в газовой фазе к поверхности жидкого металла; 2) химико-адсорбционное звено, включающее процессы диссоциации молекулярного азота, адсорбции, десорбции и др.; 3) внутреннюю диффузию - массоперенос азота в расплаве.
В реальных условиях первая стадия, как правило, осуществляется быстро и в целом скорости не лимитирует. Если процесс лимитируется второй стадией и, в частности, скоростью диссоциации молекул азота на атомы и адсорбцией последних на поверхности расплава, то кинетическое уравнение имеет вид
d[N]/dt = К1 pN2 - К2[N]2, (4.17)
К1 pN2 и К2[N]2 характеризуют скорости прямого и обратного процессов.
Поскольку pN2 = КN[N]2 и в состоянии равновесия К1 pN2 = К2[N]2, откуда KN = К1 /К, то
d[N]/dt = (К1 /К2 ) ( 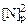 - [N]2) , (4.18)
- [N]2) , (4.18)
где [N]р и [N] – равновесная и текущая концентрации азота.
Интегрируя уравнение (4.18) в пределах от 0 до t и [N]р и [N], имеем
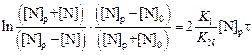 . (4.19)
. (4.19)
Если лимитирующей стадией является массоперенос в жидком металле, то
d[N]/dt = bN([N]p - [N]), (4.20)
где [N]p и [N] - концентрации азота в поверхностном слое границы металл–газ (равновесная с газовой фазой) и в объеме металла. В результате интегрирования получим
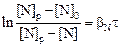 . (4.21)
. (4.21)
Решение. Представим экспериментальные результаты (для плавок А и Б ) по кинетике растворения азота на двух графиках. На первом (рис. 1) в соответствии с уравнением (4.21) по оси ординат отложим 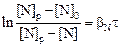 , а по оси абсцисс - время t. На втором графике (рис. 2) в соответствии с уравнением (4.19) отложим
, а по оси абсцисс - время t. На втором графике (рис. 2) в соответствии с уравнением (4.19) отложим 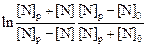 против t. Видно, что на первом графике
против t. Видно, что на первом графике
опытные данные плавки А ложатся на прямую линию, т.е. соответствуют кинетическому решению (4.21). Это означает, что в рассматриваемом случае процесс абсорбции азота лимитируется внутренней диффузией, т.е. массопереносом в расплаве. Линейная зависимость на рис. 2 относится к экспериментальным точкам плавки Б. Известно, что с увеличением степени окисленности расплава скорость абсорбции лимитируется не внутридиффузионным, а кинетическим звеном. Таким образом, в плавке Б процесс поглощения азота лимитируется химико-адсорбционным звеном.
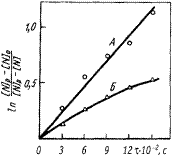 Рис. 1. Зависимость ln
Рис. 1. Зависимость ln 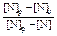 от t от t
| 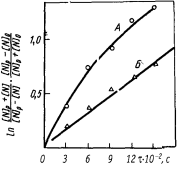 Рис. 2. Зависимость
Рис. 2. Зависимость 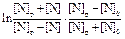 от t от t
|
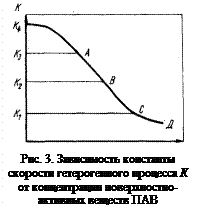 Примечания. Оценим роль ПАВ. График, отражающий влияние поверхностно-активных веществ (ПАВ) на константу скорости гетерогенного процесса, обычно имеет вид, показанный на рис. 3. Изменение значения К от K1 до К3 (при % ПАВ ® 0) соответствует увеличению константы массопереноса в результате уменьшения диффузионного сопротивления, вызванного усилением перемешивания расплава. Значение К4 соответствует предельному значению К при полностью устраненном диффузионном сопротивлении. В этом случае влияние ПАВ на К описывается линиями К4АВСД, К3АВСД, К2ВСД, К1СД. В первом случае (К4АВСД) процесс протекает в кинетическом режиме и влияние ПАВ проявляется с малых концентраций. В последующих случаях процесс, протекающий в диффузионном режиме, добавками ПАВ смещается в сторону кинетического режима. Для этого необходимы добавки ПАВ, соответствующие точкам А, В, С. Таким образом, горизонтальные участки линий К3А, K2B и K1C соответствуют диффузионной области взаимодействия. С выходом на линию ABCD процесс протекает в кинетическом режиме.
Примечания. Оценим роль ПАВ. График, отражающий влияние поверхностно-активных веществ (ПАВ) на константу скорости гетерогенного процесса, обычно имеет вид, показанный на рис. 3. Изменение значения К от K1 до К3 (при % ПАВ ® 0) соответствует увеличению константы массопереноса в результате уменьшения диффузионного сопротивления, вызванного усилением перемешивания расплава. Значение К4 соответствует предельному значению К при полностью устраненном диффузионном сопротивлении. В этом случае влияние ПАВ на К описывается линиями К4АВСД, К3АВСД, К2ВСД, К1СД. В первом случае (К4АВСД) процесс протекает в кинетическом режиме и влияние ПАВ проявляется с малых концентраций. В последующих случаях процесс, протекающий в диффузионном режиме, добавками ПАВ смещается в сторону кинетического режима. Для этого необходимы добавки ПАВ, соответствующие точкам А, В, С. Таким образом, горизонтальные участки линий К3А, K2B и K1C соответствуют диффузионной области взаимодействия. С выходом на линию ABCD процесс протекает в кинетическом режиме.
42. Диффузия серы в жидком железе
Задача. С помощью радиоизотопа серы капиллярным методом определить коэффициент диффузии серы в жидком железе и его температурную зависимость.
Исходные данные. На поверхность жидкого расплава (Х = 0), находящегося в корундовом капилляре длиной 0,1 м и диаметром 0,001 м, осторожно положили кусочек железа с радиоактивным изотопом S35. Капилляр выдержали при заданной температуре в течение 4 ч. Затем образец быстро охладили, металлический стержень разделили на кусочки и в каждом из них по радиоактивности определили концентрацию серы [% S] на расстоянии Х от поверхности расплава. Результаты этих определений приведены в таблице.
| Расстояние X от источника S35, м | Значения [% S] при темпертауре T, К | |||
| 1823 | 1873 | 1923 | 1973 | |
| 0,02 | 0,213 | 0,208 | 0,204 | 0,1995 |
| 0,04 | 0,133 | 0,135 | 0,135 | 0,136 |
| 0,06 | 0,062 | 0,065 | 0,068 | 0,071 |
| 0,08 | 0,021 | 0,024 | 0,026 | 0,029 |
| 0,10 | 0,005 | 0,006 | 0,008 | 0,009 |
Теория. Рассматриваемая задача соответствует решению второго уравнения Фика [28]
дс/дt = D(д2с/дХ 2) (4.22)
для диффузии вещества в полубесконечном образце при следующих начальных и краевых условиях:
с(Х, 0) = (g/S)d(X); [дс(0, t)]/дХ = 0, (4.23)
где g - общее количество диффундирующего вещества; S - площадь образца; d(X) - частный случай функции Дирака при Х0 = 0, которая имеет следующие свойства:
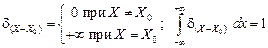 .
.
В результате интегрирования второго уравнения Фика (4.22) при указанных начальных условиях (4.23) получим
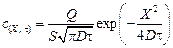 (4.24)
(4.24)
и в результате логарифмирования
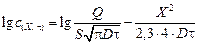 . (4.25)
. (4.25)
Отложив экспериментальные данные в координатах lgс - X 2, получим прямую, по угловому коэффициенту (tga) которой можно определить коэффициент диффузии.
Энергию активации определяем по угловому коэффициенту прямой, построенной в координатах lg D - (1/T ).
Решение. По экспериментальным данным строим график зависимости lg с от X 2 для четырех температур и находим значения tg a, тогда D = -(2,303×4t tga)-1. При 1823 К tga = -168, тогда
D = (2,3×4×4×3600×168)-1 = 4,5×10-8 м2/с .
При 1873 К D = 4,8×10-8 м2/c; при 1923 К D = 5,1×10-8 м2/с; при 1973 К D = 5,4×10-8 м2/с.
Полученные значения откладываем в координатах lgD - (1/T ) и по угловому коэффициенту прямой (tgb) определяем энергию активации диффузии: Е = -2,3Rtgb = -2,3×8,31 (-0,2400) = 45870 Дж/моль.
43. Кинетические характеристики окисления серы из жидкого железа
Задача. Определить лимитирующую стадию и кинетические характеристики окисления серы из жидкого железа кислородом газовой фазы с учетом поверхностно-активных свойств серы.
Исходные данные. Ниже приведены данные, характеризующие изменение концентрации серы в жидком железе при 1873 К. Плавка проведена в алундовом тигле при обдуве поверхности расплава газообразным кислородом.
| t, мин | 0 | 5 | 10 | 15 | 20 | 30 |
| [S], % | 0,151 | 0,130 | 0,113 | 0,102 | 0,092 | 0,076 |
Теория. В ряде случаев сера, содержащаяся в жидкой стали, окисляется на границе раздела металл–газовая фаза. Такие условия, в частности, реализуются при продувке металла кислородом. Поскольку сера является капиллярно-активным элементом, то поверхностная концентрация отличается от объемной. Исходя из этого, в кинетическое уравнение окисления серы следует подставить не объемную, а поверхностную концентрацию (допуская, что доставка серы из объема расплава на поверхность присходит значительно быстрее, чем ее окисление).
Для разбавленного раствора поверхностную концентрацию серы 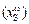 можно вычислить по формуле
можно вычислить по формуле
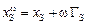 ,
,
где GS - величина адсорбции по уравнению Лангмюра
GS = (zb[S]об)/(1 + b [S]об );
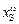 и xS - мольные доли серы в поверхностном слое и в объеме расплава.
и xS - мольные доли серы в поверхностном слое и в объеме расплава.
Для разбавленного раствора xS = [% S]MFe /100MS , тогда поверхностная концентрация серы
[S]пов = [S]об + 100 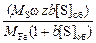 .
.
В этом случае кинетическое уравнение окисления серы кислородом газовой фазы с парциальным давлением рO2 имеет вид
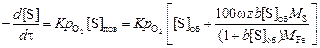 . (4.26)
. (4.26)
Поскольку сера характеризуется высокой поверхностной активностью, то
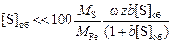 .
.
Тогда
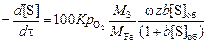 . (4.27)
. (4.27)
После интегрирования уравнения (4.26) в пределах [S]исх – [S] и 0 – t имеем
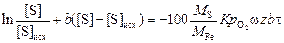 ,
,
где [S] = [S]об ;
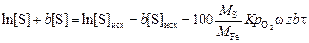 . (4.28)
. (4.28)
Экспериментальные данные, отложенные на графике зависимости ln [S] + b [S] от t, аппроксимирующиеся прямой линией, указывают на выполнимость уравнения (4.28).
Если окисление серы происходит в режиме максимальной адсорбции, т.е. в условиях, когда диффузионная доставка серы из объема расплава на поверхность не лимитирует процесса в целом, то реакция протекает с постоянной скоростью. При заданном значении рO2 этому соответствует нулевой порядок реакции по сере.
Это выполняется при b[S] > 1. Тогда правая часть уравнения (4.27) является постоянной величиной - d[S]/d t = const.
С уменьшением объемной концентрации до значения [S], при котором b[S] << 1, наблюдается изменение концентрации серы по экспоненциальному закону.
Решение. Для построения графика зависимости ln[S] + b[S] от t должно быть известно b. Воспользуемся значением b = 289 из задачи 32. Результаты расчетов приведены в таблице.
| t, с | [S] | -ln[S] | b[S] | ln[S] + b[S] |
| 0 | 0,151 | 1,89 | 43,64 | 41,75 |
| 5 | 0,130 | 2,04 | 37,57 | 35,53 |
| 10 | 0,113 | 2,18 | 32,66 | 30,48 |
| 15 | 0,102 | 2,28 | 29,42 | 27,14 |
| 20 | 0,092 | 2,38 | 26,59 | 24,21 |
| 30 | 0,076 | 2,58 | 21,96 | 19,38 |
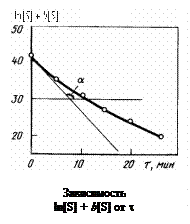 Из рисунка, построенного по приведенным данным, видно, что экспериментальные данные на прямую не ложатся. С ростом t отклонения от прямой, касательной к кривой в точке
Из рисунка, построенного по приведенным данным, видно, что экспериментальные данные на прямую не ложатся. С ростом t отклонения от прямой, касательной к кривой в точке
t = 0, возрастают.
Отклонения опытных точек от прямой в основном связаны с тем, что реакция окисления серы кислородом газовой фазы протекает в диффузионном режиме. Следовательно, поверхностная концентрация на самом деле отлична от той, которая определяется уравнением Лангмюра.
Константа скорости окисления при b[S] >> 1, равная
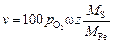 ,
,
характеризует скорость окисления при максимальной адсорбции. Для вычисления v должно быть известно КрO2 , которое можно определить из углового коэффициента прямой (4.26) (tg a = l).
Тогда v = 1,25/289 = 0,0043 %/мин.
Примечания. 1. При окислении газообразным кислородом поверхностно-активного компонента (серы) процесс может реализоваться в трех режимах: 1) максимальной адсорбции (этому соответствует постоянство скорости окисления); 2) по схеме, соответствующей уравнению (4.26) (концентрация на поверхности снижается в соответствии с объемной); 3) в области внутренней диффузии (процесс лимитируется доставкой серы на границу раздела металл–газ).
2. Строгое решение задачи требует также учета влияния поверхностно-активного кислорода на концентрацию серы по границе раздела фаз, которое в настоящей задаче не учитывалось.
44. Диффузия кальция в жидком шлаке
Задача. Капиллярным методом определить коэффициент диффузии кальция в жидком шлаке (40 % СаО, 40 % SiO2 и 20 % Аl2O3) при 1873 К.
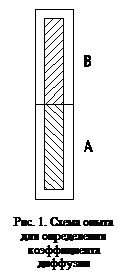 Исходные данные. Капилляр А, содержащий шлаковый расплав с радиоактивным изотопом Са45 с исходной концентрацией c0 = 2,7 мкКи и приводили в контакт с капилляром В, содержащим тот же шлак, но без изотопа (рис. 1). Через
Исходные данные. Капилляр А, содержащий шлаковый расплав с радиоактивным изотопом Са45 с исходной концентрацией c0 = 2,7 мкКи и приводили в контакт с капилляром В, содержащим тот же шлак, но без изотопа (рис. 1). Через
6 ч выдержки образец закаливали и определяли распределение изотопа Са45 по длине капилляра В. Полученные данные приведены в табл. 1.
Теория. Для того чтобы вычислить D по экспериментальным данным, необходимо решить второе диффузионное уравнение Фика:
¶с/¶t = D (¶2с/¶Х 2). (4.29)
Таблица 1
| Расстояние Х от источника Са45, м | Активность изотопа, мкКи | Расстояние Х от источника Са45, м | Активность изотопа, мкКи |
| 0,0005 | 1,041 | 0,0025 | 0,196 |
| 0,0010 | 0,7556 | 0,0030 | 0,1073 |
| 0,0015 | 0,5138 | 0,0035 | 0,0563 |
| 0,0020 | 0,3286 | 0,0040 | 0,0265 |
Для диффузии из полубесконечного образца (капилляр А) с начальной концентрацией с0 в полубесконечный образец (капилляр В) с нулевой исходной концентрацией начальные условия имеют вид
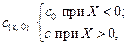 (4.30)
(4.30)
где c(х, 0) - концентрация в точке Х при t = 0.
В этом случае решением уравнения (4.29) является
с = (с0 /2) [1 - f (Х/2 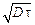 )], (4.31)
)], (4.31)
где f(z) - интеграл Лапласа (функция Гаусса),
f(z) = 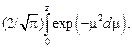
Этот интеграл в элементарных функциях не берется, и его значения в зависимости от величины z приведены в таблицах [28].
Решение. Коэффициент диффузии определяем по уравнению (4.31). Поскольку интенсивность излучения изотопа Са45 пропорциональна концентрации кальция в шлаке, то в уравнение (4.31) вместо концентрации с и с0 подставляем соответствующие активности изотопов, полученной на основе опыта. Для Х = 0,005 м имеем
1,041 = (2,7/2) [1 - (Х/2 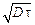 )],
)],
откуда 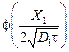 = 0,2289.
= 0,2289.
Зная величину f(z) = 0,2289, по таблице [28] находим
z = 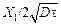 = 0,205,
= 0,205,
откуда D1 = 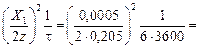 6,9×10-11 м2/c.
6,9×10-11 м2/c.
Величины D, найденные для других значений X, приведены в табл. 2.
Таблица 2
| Расстояние Х от источника Са45, м | D ×10–11, м/с2 | Расстояние Х от источника Са45, м | D ×10–11, м/с2 |
| 0,0005 | 6,9 | 0,0025 | 6,82 |
| 0,0010 | 6,72 | 0,0030 | 6,77 |
| 0,0015 | 6,77 | 0,0035 | 6,84 |
| 0,0020 | 6,80 | 0,0040 | 6,80 |
Среднее значение коэффициента диффузии
D = 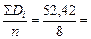 6,55×10-11 м2/с.
6,55×10-11 м2/с.
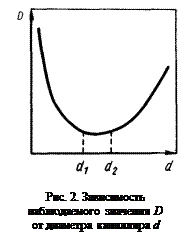 Примечание. Применение капилляров, как это сделано в настоящей задаче, позволяет существенно подавить конвекцию. Для того чтобы убедиться, что конвекция в достаточной мере устранена, опыты проводят в капиллярах различного диаметра (d). Затем строят график зависимости наблюдаемого значения D от d. Полученная зависимость представлена на рис. 2. Повышенное значение D при малых d связано с определяющим вкладом поверхностной диффузии. Рост D при увеличении d после точки минимума связан с развитием конвекции. Таким образом, интервал диаметров d1 – d2 является наиболее подходящим для определения D капиллярным методом.
Примечание. Применение капилляров, как это сделано в настоящей задаче, позволяет существенно подавить конвекцию. Для того чтобы убедиться, что конвекция в достаточной мере устранена, опыты проводят в капиллярах различного диаметра (d). Затем строят график зависимости наблюдаемого значения D от d. Полученная зависимость представлена на рис. 2. Повышенное значение D при малых d связано с определяющим вкладом поверхностной диффузии. Рост D при увеличении d после точки минимума связан с развитием конвекции. Таким образом, интервал диаметров d1 – d2 является наиболее подходящим для определения D капиллярным методом.
45. Определение кинетических характеристик методом вращающегося диска
Задача. На основе экспериментальных данных, полученных при вращении графитового диска в расплаве, определить коэффициент диффузии углерода и константу скорости растворения графита в жидком железе.
Исходные данные. Образцы для растворения в виде таблеток диаметром 10 мм из пирографита и поликристаллического графита закрепляли в алундовые оправы и вращали в жидком железе в течение 20–180 с. За это время концентрация углерода в расплаве изменялась на пренебрежимо малую величину. Убыль массы углерода из оправы определяли взвешиванием. Экспериментальные данные представлены на рисунке. Кинематическая вязкость железа при 1823 К составляет v = 0,0045 м2/с. Насыщенная концентрация углерода в жидком железе при 1823 К снас = 377 кг/м3.
Теория. Метод вращающегося диска [29] позволяет решить ряд задач по кинетике металлургических реакций. Изменяя число оборотов диска, можно осуществлять процесс в диффузионном, смешанном и кинетическом режимах.
Если процесс реализуется в диффузионном режиме, то из экспериментальных данных можно определить коэффициент диффузии. Особенность рассматриваемого метода заключается в том, что при определении коэффициента диффузии этим методом конвекцию не устраняют, как это делается в капиллярном методе (см. задачу 45), а количественно задают и учитывают в последующих расчетах. Увеличивая число оборотов диска, процесс можно перевести из диффузионного в кинетический режим взаимодействия.
В этом случае по экспериментальным данным можно вычислить количественные данные по скорости химической реакции, акта растворения твердых тел в жидкостях и др.
Вращающийся диск как поверхность взаимодействия обладает важной особенностью, которая отличает его от других реакционных поверхностей. Толщина гидродинамического слоя у поверхности вращающегося диска, а вместе с ней и толщина диффузионного слоя имеют постоянное значение по всей поверхности диска. Диффузия к диску (или от него) представляет случай, для которого уравнение конвективной диффузии имеет точное решение [29]. Поток вещества к поверхности диска описывается уравнением
W = 0,62D 2/3 v-1/6 w1/2 (снас - с), (4.32)
где D - молекулярный коэффициент диффузии, м2/с; w - частота вращения, с-1; cнас и с - насыщенная и текущая концентрации, кг/м3; v - кинематическая вязкость, м2/c.
Под величиной потока W понимают количество переносимого вещества (кг) от диска (или к диску) с 1 м2 за 1 с.
Зная W и другие величины, входящие в уравнение (4.32), коэффициент диффузии можно вычислить по формуле
D = 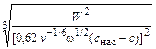 . (4.33)
. (4.33)
Если диффузионное сопротивление устранено в результате существенного развития конвекции, задаваемого вращением диска, то процесс реализуется в кинетическом режиме и скорость растворения графита определяется актом перехода атомов с поверхности твердого тела. В этом случае при с = 0 поток вещества W [кг/(м2/с)] численно равен константе скорости растворения (K1). Скорость растворения, равная потоку, является постоянной величиной W = K1. Если с ¹ 0, то W = K1 - К2с, где K2 - константа скорости осаждения. При равновесии W = 0 и K1 = К2 снас и W = K1(l - с/снас ) .
Решение. В соответствии с уравнением (4.33) результаты экспериментов представлены на рисунке в координатах W - w1/2 (w - частота вращения, равная w = 2pп, где п - число оборотов в секунду). Видно, что процесс растворения характеризуется тремя режимами: диффузионным, смешанным и кинетическим. В диффузионной области соблюдается линейная зависимость между W и w1/2. Такие условия осуществляются для поликристаллического графита до n = 33,3 с-1, а для пирографита от п = 50 с–1. Величина растворимости углерода в слое расплава, прилегающем к поверхности диска (снас), определяющая величину диффузионного потока в соответствии с уравнением (4.32), не зависит от поверхностной энергии соответствующей грани кристалла, поэтому в диффузионной области различий в скоростях растворения не наблюдается. По формуле (4.33) вычислим коэффициент диффузии углерода в жидком железе (с = 0) при 1823 К по данным рисунка (п = 10 с-1).
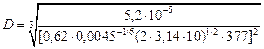 = 0,81×10–8 м2/c.
= 0,81×10–8 м2/c.
С увеличением частоты вращения диска до 70 с-1 для поликристаллического графита и до 100 с-1 для пирографита процесс растворения переходит в кинетический режим. Экспериментальным доказательством этого является независимость W от w1/2. Скорость растворения и соответственно константа скорости для поликристаллического графита при с = 0 равна К = 11×10-5 кг/(м2/с). Для пирографита с базисной плоскости (002) К = 16×10-5 кг/(м2/с). Высокая скорость растворения
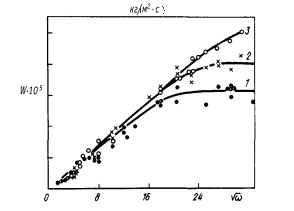
Зависимость скорости растворения углерода в расплаве Fe–С
при 1823 К от частоты вращения образца: 1 - поликристаллический графит; 2 - пирографит (базисная плоскость (002); 3 - пирографит
(торцевая плоскость)
пирографита с торцевой грани по сравнению с базисной (1,3 раза) согласуется с принципом Вульфа – Кюри. Граням кристалла с бóльшим значением коэффициента поверхностного натяжения (si) соответствует более высокая скорость растворения.