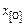Изменение состава оксидных включений в процессе итераций
| Итерация |
| Состав оксидной фазы | |||
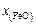
| 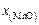
| 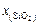
| 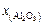
| ||
| 1 | 0,00321 | 0,01395 | 0,03122 | 0,09003 | 0,86481 |
| 2 | 0,00397 | 0,00168 | 0,01644 | 0,15236 | 0,82951 |
| 3 | 0,00398 | 0,00149 | 0,01643 | 0,15279 | 0,82930 |
| 4 | 0,00398 | 0,00148 | 0,01643 | 0,15282 | 0,82927 |
По окончании итерационного расчета определяем процентный состав оксидной фазы:
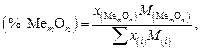 (2.63)
(2.63)
где i – оксиды, входящие в состав оксидной фазы – FeO, MnO, SiO2, Al2O3; 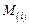 – молекулярная масса соответствующего оксида.
– молекулярная масса соответствующего оксида.
Окончательный состав оксидной фазы:
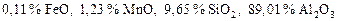 .
.
Приложение – программа расчета равновесных составов на языке Паскаль.
const
Mo = 16; {Fe Mn Si Al O C }
kk : array [1..4] of real = (4.35,21.64,4.38e4,1.05e14); {K}
qq : array [1..4] of real = (0,0,0,0); {Q}
pm : array [1..6] of real = (1,0.45,0.2,0.0005,0,0.1); {[%i]}
mm : array [1..4] of real = (1,1,1,2); {m}
nn : array [1..4] of real = (1,1,2,3); {n}
ma : array [1..5] of real = (56,55,28,27,16); {Ma}
lf : array [1..5] of real = (0,0,0,0,0); {ln(f)}
gg : array [1..4] of real = (1,1,1,1); {gamma}
kp : array [1..5] of real = (334.7,251,171.5,125,1255); {kappa}
ep : array [2..5,2..6] of real= {epsilon}
(( 0 , 0 , 0 ,-0.083,-0.07),
(0.002 ,0.11 ,0.058,-0.23 , 0.18),
( 0 ,0.0056,0.045,-6.6 ,0.091),
(-0.021,-0.131,-3.9 ,-0.2 ,-0.45)) ;
var
xl,xr,x0,lx,RT,s : real; ee : array [1..5,1..5] of real;
i,j : integer;
xs : array [1..4] of real; {x(RmOn)}
xi : array [1..5] of real; {x(i)}
la : array [1..5] of real; {ln(a(i))}
begin
RT := 1873*8.314*1e-3;
for i := 1 to 5 do for j := 1 to 5 do
ee[i,j] := exp(-sqr(sqrt(kp[i])-sqrt(kp[j]))/RT);
repeat
x0 := pm[5];
for i := 1 to 4 do
qq[i] := kk[i]*exp((ln(pm[i])+lf[i])*mm[i]+lf[5]*nn[i])/gg[i];
xl := 0; xr := 0.1;
for j := 1 to 30 do begin
pm[5] := (xl+xr)/2; lx := ln(pm[5]); s := -1;
for i := 1 to 4 do begin xs[i] := qq[i]*exp(lx*nn[i]); s := s+xs[i]; end;
if s<0 then xl := pm[5] else xr := pm[5];
end;
for i := 1 to 4 do write(xs[i]:8:5); writeln(pm[5]:8:5);
for i := 2 to 5 do begin
s := 0; for j := 2 to 6 do s := s+pm[j]*ep[i,j];
lf[i] := 2.303*s;
end;
s := 0;
for i := 1 to 4 do begin
xi[i] := xs[i]*mm[i]; s := s+xi[i]; xi[5] := xi[5]+xs[i]*nn[i]; end;
s := s+xi[5];
{for i := 1 to 5 do xi[i] := xi[i]/s;}
for i := 1 to 5 do begin
s := 0; for j := 1 to 5 do s := s+xi[j]*ee[i,j];
la[i] := ln(xi[i]/s); end;
for i := 1 to 5 do gg[i] := exp(la[i]*mm[i]+la[5]*nn[i])/xs[i];
until abs(pm[5]-x0)<1e-6;
s := 0;
for i := 1 to 4 do begin
xs[i] := xs[i]*(ma[i]*mm[i]+ma[5]*nn[i]); s := s+xs[i]; end;
for i := 1 to 4 do write(xs[i]/s*100:8:4);
writeln;
end.
28. Расчет максимальной
растворимости MgO в шлаке
Задача. Рассчитать добавку оксида магния к шлаку заданного состава для уменьшения его агрессивности по отношению к магнезитовой футеровке.
Исходные данные. 1. Состав шлака: 50 % СаО; 20 % SiO2 ; 25 % FеО; 3 % Fе2О3; 2 % МgO. 2. Температура 1873 К. 3. В качестве массива экспериментальных составов шлаков, насыщенных магнезией, использовать данные Чипмана по изучению равновесного состояния системы металл–шлак в магнезитовой футеровке, полученные при 1873 К.
Теория. Для предотвращения растворения магнезитовой футеровки в шлаке последний должен быть насыщен оксидом магния. При наличии надежных справочных данных о растворимости (активности) МgO в шлаках близкого состава (или диаграмм состояния) задачу можно было бы решить на основании условия 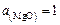 подобно задаче 25.
подобно задаче 25.
На практике, однако, часто приходится иметь дело со шлаками сложного состава, необходимые справочные данные для которых отсутствуют. В таких случаях обоснованные оценки могут быть сделаны исходя из имеющихся экспериментальных или производственных данных, относящихся к близким по составу шлакам. За стандарт при этом принимают расчетную величину 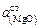 , определенную как среднюю по опытному массиву:
, определенную как среднюю по опытному массиву:
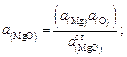 (2.64)
(2.64)
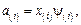 (2.65)
(2.65)
где 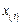 – атомная доля i-го компонента;
– атомная доля i-го компонента; 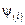 определяется по выражению (2.25).
определяется по выражению (2.25).
Решение. По формуле (2.65) находим значения 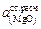 для каждого шлака заданного массива и вычисляем среднее значение:
для каждого шлака заданного массива и вычисляем среднее значение:
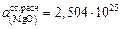 .
.
Находим аналогичную величину для заданного шлака 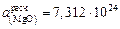 и активность, отнесенную к стандартному состоянию
и активность, отнесенную к стандартному состоянию 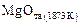 :
:
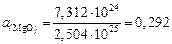 .
.
Необходимую добавку МgO к заданному шлаку определяем методом последовательного приближения. К 100 кг исходного шлака добавим 2,5 кг МgО и рассчитаем состав после добавки:
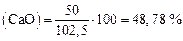 ; ;
| 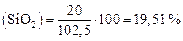 ; ;
|
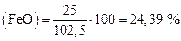 ; ;
| 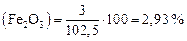 . .
|
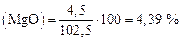 ; ;
|
Для полученного состава шлака активность МgО равна 0,630. Определяем окончательный состав шлака: 47,39 % СаО; 18,96 % SiO2 ; 23,7 % FеО; 2,84 % Fе2О3 ; 7,11 % МgО; 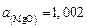 . Необходимая добавка МgO составляет 5,5 кг на 100 кг шлака.
. Необходимая добавка МgO составляет 5,5 кг на 100 кг шлака.
29. Влияние окисленности системы на степень рафинирования стали шлаковыми расплавами
Задача. Рассчитать изменение степени десульфурации низколегированной стали при обработке ее синтетическим шлаком в ковше в случае снижения содержания растворенного алюминия в металле с 0,05 до 0,001 %.
Исходные данные. 1. Температура 1823 К. 2. Состав синтетического шлака: 53 % СаО, 47 % Аl2О3. 3. Количество шлакового расплава 50 кг/т. 4. Активность Аl2О3 в шлаке a(Al2O3) = 0,56 [20]. 5. Сульфидная емкость шлака равна сS = 10-3,5 [3, 21, 22].
Теория. Степень рафинирования металла от вредных примесей при объемном одношлаковом режиме обработки в ковше описывается уравнением [23]:
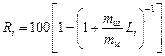 , (2.66)
, (2.66)
где Ri = 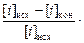 100 %; mш/mм (кратность шлака l) - отношение масс шлака и металла; Li = (i)/[i] - коэффициент распределения i-й примеси между шлаковой и металлической фазами.
100 %; mш/mм (кратность шлака l) - отношение масс шлака и металла; Li = (i)/[i] - коэффициент распределения i-й примеси между шлаковой и металлической фазами.
Величина Li определяется составом и температурой шлака и в значительной степени зависит от уровня окисленности системы, которая характеризуется значением равновесного парциального давления кислорода рO2 в системе [3]:
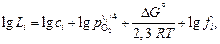 (2.67)
(2.67)
где с i - сорбционная емкость шлака по отношению к i-й примеси;
v i - валентность данной примеси в шлаке (в рассматриваемом случае - 2 для серы); DGº – изменение стандартной энергии Гиббса для реакции 1/2 i2(г) = [i]1 % p; fi – коэффициент активности i-го компонента в металлическом расплаве.
Сульфидная емкость шлакового расплава определяется следующим соотношением [3]:
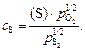 (2.68)
(2.68)
Значения cS для различных шлаков находят, как правило, из экспериментальных данных или рассчитывают на основе эмпирических зависимостей.
Решение. Величину рO2 в системе можно оценить по реакции распределения алюминия между металлическим и шлаковым расплавами:
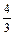 [Аl] + О2 =
[Аl] + О2 = 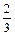 (А12O3). (2.69)
(А12O3). (2.69)
Тогда из выражения для константы равновесия данной реакции получим
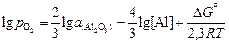 . (2.70)
. (2.70)
С учетом того, что изменение стандартной энергии Гиббса данной реакции при 1823 К DGo = -592450 Дж/моль [3], для стали с 0,05 % [Аl] получим
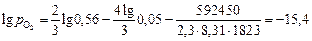 ,
,
а при содержании в металле 0,001 % [Аl] lg рO2 = -13,0 (рO2 , атм).
В соответствии с выражением (2.67) и значением DGo для реакции 1/2 S2(г) = [S] по данным работы [3] для первого случая
lg LS = lg cS -  lg рO2 +
lg рO2 + 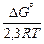 + lg fS = -3,5 +
+ lg fS = -3,5 + 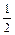 ×15,4 –
×15,4 –
– 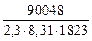 + lg1 = 1,72 и LS = 53.
+ lg1 = 1,72 и LS = 53.
Значения степени рафинирования стали с 0,05 % [Аl] от серы (RS) при обработке в ковше составит RS = 100[1 - (1 + 0,05×53)-1] = 73 %, т.е. в этих условиях десульфурация металла протекает достаточно успешно. При возрастании уровня окисленности системы до
рO2 = 10-13 атм (0,001 % [Аl] в металле) LS снижается до 3,5. При этом RS = 16,5 %. Таким образом, полученные результаты показывают, что практически не изменяя состава рафинировочных шлаков, а регулируя только уровень окисленности системы, можно существенно повысить степень рафинирования стали от вредных примесей при внепечной обработке.
30. Расчет распределения хрома
между металлом и шлаком
при электрошлаковом переплаве
Задача. ЭШП сталей типа ШХ15, содержащих 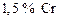 , осуществляется с использованием шлаков с высоким содержанием фторида кальция. Определить, как изменится коэффициент распределения хрома при ЭШП стали под флюсом АНФ-29.
, осуществляется с использованием шлаков с высоким содержанием фторида кальция. Определить, как изменится коэффициент распределения хрома при ЭШП стали под флюсом АНФ-29.
Исходные данные. 1. Составы металла, шлака опытных плавок при 1873 К (плавки 1–4) и состав исходного промышленного флюса АНФ-29 приведены в таблицах. 2. Степень окисленности металла считается постоянной.
| Плавка | Состав металла, % масс. | ||||
| Si | Mn | S | O | Cr | |
| 1 | 0,21 | 0,45 | 0,018 | 0,0033 | 1,47 |
| 2 | 0,29 | 0,45 | 0,017 | – | 1,48 |
| 3 | 0,11 | 0,37 | 0,013 | 0,0035 | 1,38 |
| 4 | 0,29 | 0,45 | 0,017 | – | 1,48 |
| Плавка | Состав шлака и флюса, % масс. | |||||||
| СаО | Al2O3 | SiO2 | МnО | Fе2O3 | S | Cr2O3 | CaF2 | |
| 1 | 8,12 | 4,64 | 3,02 | 0,30 | 0,41 | 0,015 | 0,15 | 83,17 |
| 2 | 6,11 | 8,18 | 2,88 | 0,28 | 0,25 | 0,028 | 0,13 | 78,46 |
| 3 | 8,14 | 7,99 | 3,50 | 0,25 | 0,66 | 0,021 | 0,30 | 78,00 |
| 4 | 8,08 | 7,55 | 4,42 | 0,16 | 0,41 | 0,028 | 0,15 | 77,40 |
| Флюс АНФ-29 | 35 | 15 | 15 | – | – | – | – | 35 |
Теория. Константа распределения хрома по кислороду между шлаковой и металлической фазами определяется по уравнениям (см. задачу 24):
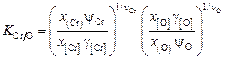 ; (2.71)
; (2.71)
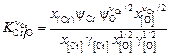 . (2.72)
. (2.72)
В условиях неизменной окисленности 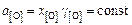 , поэтому уравнение (2.72) можно записать в следующем виде:
, поэтому уравнение (2.72) можно записать в следующем виде:
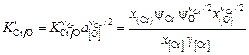 . (2.73)
. (2.73)
Из-за переменной валентности хрома форма существования его в расплаве шлака может быть различной. Предположим, что 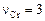 . Под коэффициентом распределения хрома между шлаком и металлом принято понимать выражение
. Под коэффициентом распределения хрома между шлаком и металлом принято понимать выражение
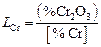 . (2.74)
. (2.74)
Связь между процентным содержанием и атомной долей элемента выражается соотношением
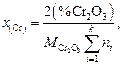 (2.75)
(2.75)
где 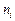 – число атомов i-го элемента в 100 г шлака;
– число атомов i-го элемента в 100 г шлака; 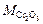 – молекулярная масса Сr2O3 .
– молекулярная масса Сr2O3 .
Откуда получаем
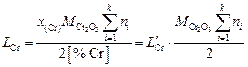 , (2.76)
, (2.76)
где
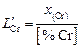 . (2.77)
. (2.77)
Связь между 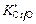 и
и 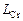 определяется соотношением
определяется соотношением
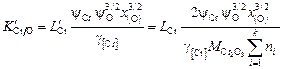 . (2.78)
. (2.78)
Алгоритм решения
1. По известным данным о составе контактирующих фаз для каждой плавки находим х(O) , х(Cr) , yO , yCr (см. задачу 24), g[Cr] определяем с помощью параметров взаимодействия Вагнера, LCr и KCr/O по уравнениям (2.74) и (2.78). Полученные результаты приведены в таблице.
| Плавка | 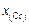
| 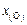
| 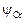
| 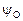
| 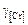
| 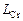
| 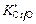
|
| 1 | 0,0005 | 0,1021 | 1,245×104 | 9,897×1028 | 0,8098 | 0,1020 | 5,29×1042 |
| 2 | 0,0005 | 0,1198 | 1,254×104 | 9,907×1028 | 0,7492 | 0,0878 | 7,3123×1042 |
| 3 | 0,0010 | 0,1336 | 8,896×103 | 1,188×1029 | 0,8943 | 0,2174 | 1,315×1043 |
| 4 | 0,0005 | 0,1358 | 8,951×103 | 1,125×1029 | 0,7492 | 0,1014 | 7,6152×1042 |
| Средняя арифметическая величина | 0,8006 | 0,1272 | 8,3419×1042 | ||||
2. Находим средние арифметические значения величин 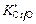 и
и 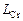 :
:
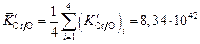 ;
;
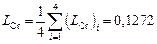 .
.
3. Оценим ошибку, вносимую в расчеты величины 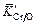 .
.
Выборочная дисперсия
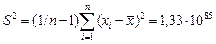 .
.
Среднее квадратическое отклонение
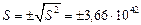 .
.
Коэффициент вариации
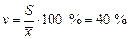 .
.
Ошибка среднего арифметического
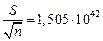 .
.
Критерий Стьюдента для 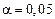 и
и 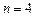 равен
равен 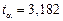 . Абсолютная погрешность
. Абсолютная погрешность
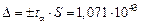 .
.
Относительная погрешность
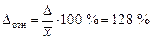 .
.
Для уменьшения ошибки оценки 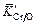 необходимо использовать более обширные массивы экспериментальных данных.
необходимо использовать более обширные массивы экспериментальных данных.
4. Вычисляем концентрацию кислорода и коэффициенты активности хрома и кислорода для флюса АНФ-29 (см. задачу 24): 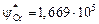 ;
; 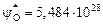 ;
; 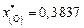 ;
; 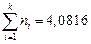 .
.
5. Коэффициент активности хрома в металле принимаем равным средней арифметической величине 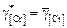 , рассчитанной по известным данным (п. 1 данного алгоритма):
, рассчитанной по известным данным (п. 1 данного алгоритма):
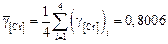 .
.
Для известной марки стали 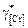 вычисляют по химическому составу.
вычисляют по химическому составу.
6. По вычисленным значениям 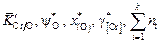 находим коэффициент распределения хрома при переплаве под флюсом АНФ-29 в соответствии с уравнением (2.78):
находим коэффициент распределения хрома при переплаве под флюсом АНФ-29 в соответствии с уравнением (2.78):
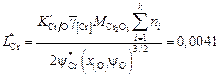 .
.
При замене флюса с высоким содержанием фторида кальция флюсом АНФ-29 коэффициент распределения хрома уменьшается.
7. Поскольку в зависимости от степени окисленности валентность хрома изменяется, приведенные выше вычисления повторим для случая более низкой валентности хрома: 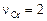 . Основные результаты расчета:
. Основные результаты расчета:
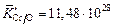 ;
; 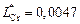 .
.
И в этом случае коэффициент распределения хрома также меньше, чем при использовании флюса с высоким содержанием фторида кальция. Приведенный пример показывает, как на основании имеющихся экспериментальных данных по распределению элементов между фазами можно оценить изменение коэффициента распределения при изменении состава шлака и постоянной степени окисленности металла.
Численные значения промежуточных результатов, приведенных в алгоритме решения, могут быть использованы в качестве контрольных при отладке программы.
31. Окислительная дефосфорация
при плавке стали
Задача. Определить степень дефосфорации и конечную (см. задачу 28) концентрацию фосфора в стали, находящейся под шлаком заданного состава при 1873 К.