Исходные данные. 1. Состав шлака: 50 % СаО, 50 % SiO2. 2. За стандартное состояние принят -кристобалит. 3. Температура 1873 К.

Дата: 2025-05-01; Просмотры: 2
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

Теория. Расчет активностей компонентов кислых и некоторых других шлаковых систем, характеризующихся сильным взаимодействием компонентов, представляет определенные трудности и требует применения более сложных расчетных формул. Ранее использованная формула модели коллективизированных электронов (МКЭ) (см. задачу 24) для вычисления коэффициентов активности исходит из атермального приближения (не содержит энтальпийного члена), поэтому ее применимость ограничена шлаками с содержанием 30–40 % SiO2.

Более полная формула [19]:

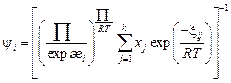(2.25)

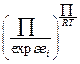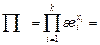
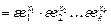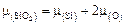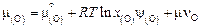включает дополнительный множитель , где . (Остальные обозначения прежние, см. задачу 24.) Учитывая, что , где и 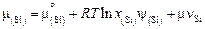, а также принимая 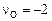, , 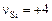находим

.

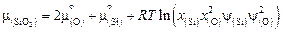Сравнивая это выражение с общим определением активности 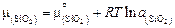, находим

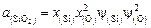. (2.26)

Подставив в выражение (2.26) значения коэффициентов активности согласно уравнению (2.25), получим

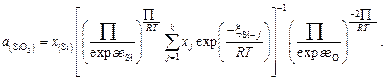(2.27)

При выводе выражения (2.27) учтено, что 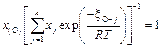, в чем нетрудно убедиться, подставив численные значения .

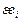Найденное по формулам (2.26), (2.27) значение активности относится к некоторому стандартному состоянию, определяемому неизвестной величиной .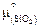

Приведение расчетных значений к тому или иному выбранному стандартному состоянию основано на том, что в фазе, состав которой принят за стандартный по компоненту i, его активность должна быть равна 1. Для нормирования (приведения к заданному стандарту) активности необходимо найти ее численное значение в данном растворе и отнести его к вычисленной тем же методом активности в стандартном состоянии:

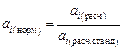. (2.28)

В соответствии с условием задачи стандартным 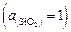является расплав системы 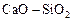, находящейся при 1873 К в равновесии с 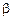-кристобалитом. Пользуясь диаграммой состояния системы , находим, что при этой температуре в равновесии с кристобалитом находится расплав с массовым содержанием 32,9 % СаО и 67,1 % SiO2 , поэтому нормированная на заданный стандарт активность SiO2 в шлаке, содержащем 50 % СаО и 50 % SiO2, равна

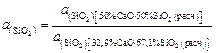
или

.

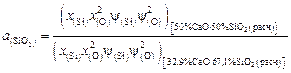Решение. Выразим в атомных долях заданный состав шлака (алгоритм пересчета см. в задаче 24): 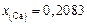, , 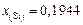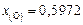и стандартный , , .

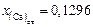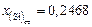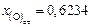Вычислим значения коэффициентов активности по формуле (2.25). Ниже приведены численные значения составляющих этой формулы для контроля. Для шлака с массовым содержанием 32,9 % СаО и 67,1 % SiO2

, ,
;

.

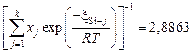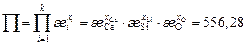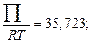
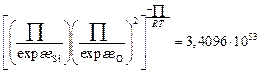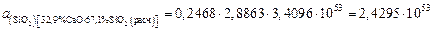Для шлака с массовым содержанием 50 % СаО и 50 % SiO2

, , ,
;
,
.

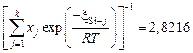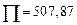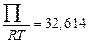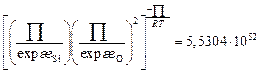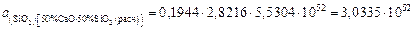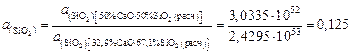Примечание. Формула (2.25) имеет повышенную чувствительность к значениям параметров 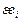, поэтому приводимые в литературе [3] их величины могут быть использованы лишь для грубых оценок. Для повышения точности расчетов формулу (2.25) следует использовать как аппроксимирующую функцию. При этом с помощью статистической обработки массива надежных экспериментальных данных уточняют значения параметров 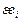, а затем их используют для расчетов. Очевидно, что эффективное применение полученных таким путем величин 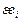ограничивается составами шлаков, близких к составам шлаков массива. На основании имеющихся данных об активностях компонентов шлаков с повышенным содержанием SiO2 были получены значения, использовавшиеся в рассмотренной задаче (числитель – ккал, знаменатель – кДж):

Са Fe А1 Мg Мn Si О

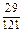
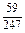
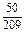
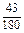
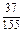
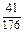
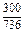
26. Десульфурация стали шлаком

Задача. Рассчитать конечную концентрацию серы в стали, находящейся под восстановительным шлаком заданного состава.

Исходные данные. 1. Состав металла (трансформаторная сталь): 0,03 % С; 3 % Si; 0,005 % Р; 0,015 % S; 0,011 % А1; 0,0034 % O. 2. Состав шлака: 47 % СаО; 14 % МgО; 18 % SiO2; 5 % Аl2О3;
14 % СаF2; 0,2 % МnО; 0,8 % FеО. 3. Кратность шлака l = 3 %.

Теория. Реакция десульфурации имеет вид

[S] + (СаО) = (СаS) + [О]. (2.29)

Из выражения константы равновесия К1 получим1

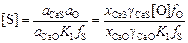. (2.30)

Видно, что более полной десульфурации способствует высокая активность СаО в шлаке и серы в металле, низкая окисленность системы aO, а также пониженная активность СаS в шлаке. Из уравнения (2.30) получим выражение для равновесного коэффициента распределения серы L = (S)/[S]. Для этого выразим хCaS через концентрацию серы в шлаке (% S):

хCaS = (% S)/(32Sn) , (2.31)

где 32 - относительная атомная масса серы; Sn - сумма молей компонентов (СаО, СаS, SiO2 и др.) в 100 г шлака.

Подставив выражение (2.31) в формулу (2.30), получим

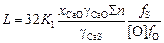. (2.32)

В результате логарифмирования выражения (2.32)

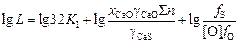. (2.33)

В выражении (2.33) первое слагаемое является при заданной температуре постоянной величиной, второе слагаемое определяется составом применяющегося шлака, а третье - составом металла: активностью в нем серы и кислорода.

При рафинировании жидкого железа можно принять fO = 1 и fS = 1. Тогда формула (2.33) приобретает вид

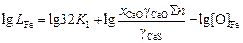. (2.34)

При экспериментальном изучении распределения серы между жидким железом и шлаками системы СаО–МgO–Аl2O3–SiO2 для коэффициента распределения LFe получено эмпирическое уравнение, имеющее ту же структуру, что и уравнение (2.34):

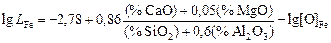. (2.35)

Если теми же шлаками рафинировать не железо, а сплав на его основе, то связь между коэффициентами распределения LFe и Lспл можно получить, записав выражение константы равновесия реакции (2.29) отдельно для десульфурации железа и сплава:

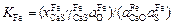; (2.36)

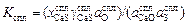. (2.37)

Поскольку очевидно, что KFe = Kспл , то равны и правые части выражений (2.36) и (2.37):

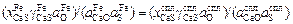. (2.38)

Допустим, что 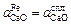и 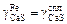. Тогда, подставив формулу (2.31) в уравнение (2.38) и произведя необходимые преобразования, получим

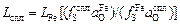. (2.39)

Учитывая, что 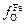» 1 и 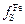» 1, в результате логарифмирования выражения (2.39) получаем

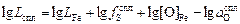. (2.40)

Подставив в уравнение (2.40) выражение (2.35) и проведя необходимые преобразования, получим

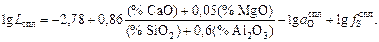(2.41)

По известным значениям 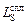, кратности шлака l, начальному содержанию серы в стали [S]н и шлаке (S)н можно определить равновесную конечную концентрацию серы в стали [S]. Для этого составим и решим систему уравнений

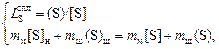
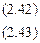
где mм и mш - массы металла и шлака.

Выражение (2.43) является уравнением материального баланса и составлено при условии, что сера перераспределяется между металлом и шлаком и не выделяется в газовую фазу. Если в ходе рафинирования величины mм и mш не изменяются, то получаем следующее решение системы уравнений:

[S] = (100[S]н + l(S)н)/(100 + 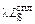), (2.44)

где l - кратность шлака, %; l = (mш/mм)100 %.

Степень десульфурации

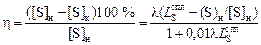. (2.45)

Решение. По формуле (2.41) вычислим 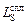при 1873 К. Для этого предварительно найдем аO = [О]fO и значение fS , входящее в формулу (2.41). Вследствие высокого содержания кремния в металле (3 %) будем считать, что аO определяется реакцией раскисления металла кремнием:

[Si] + 2[О] = SiO2 (тв) . (2.46)

Согласно данным [3] температурная зависимость константы равновесия реакции равна

lgК2 = (31100/T ) - 12,0. (2.47)

Запишем выражение константы равновесия:

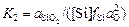. (2.48)

Из уравнения (2.48) получим

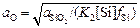. (2.49)

При 1873 К К2 = 4×104. Значение fSi , вычисленное по параметрам взаимодействия (см. задачу 16 и табл. П3), равно fSi = 2,05. Если принять, что продукты раскисления металла представлены чистым кремнеземом, то aSiO2 = 1. Тогда по формуле (2.49) получим

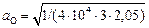= 0,0020 %.

Значение 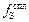, найденное по параметрам взаимодействия (см. табл. П3), равно 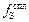= 1,5. Теперь по формуле (2.41) вычислим Lспл :

,

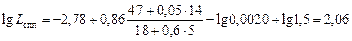т.е. расчетное значение Lспл = 115. Экспериментально получаемые при выплавке трансформаторной стали значения Lспл колеблются от 80 до150 и достаточно хорошо согласуются с расчетной величиной Lспл = 115.

По формуле (2.44) рассчитаем концентрацию серы в металле после обработки шлаком:

[S] = (100×0,015 + 3×0,04)/(100 + 3×115) = 0,0036 %.

По формуле (2.45) вычислим степень десульфурации:

h = [(0,015 - 0,0036)100 %]/0,015 = 76 %.

27. Равновесный состав оксидных включений, взвешенных в жидкой стали

Задача. Определить содержание кислорода, растворенного в металле при 1873 К, и равновесный состав оксидной фазы, диспергированной в нем в виде неметаллических включений.