Исходные данные. Состав шлака: 30,3 % СаО; 28,2 % SiO2; 40,4 % Аl2O3. Содержание углерода в металле 2,62 %.
Теория. Содержание кремния в металле находим из равновесия реакции: 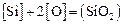 .
.
По данным табл. П9 получим
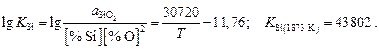
Значение  определим по выражению для константы равновесия реакции
определим по выражению для константы равновесия реакции 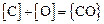 (см. табл. П9):
(см. табл. П9):
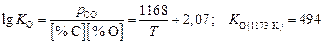 .
.
Решение. Выразим мольный состав шлака (расчет аналогичен расчету задачи 22): 38,45 % СаО; 33,4 % SiO2; 28,14 % Аl2O3. По диаграмме (см. рисунок) находим 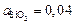 . Определяем содержание кислорода в металле, принимая
. Определяем содержание кислорода в металле, принимая 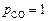 атм:
атм:
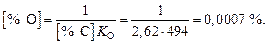
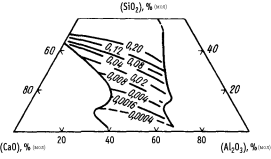
Активность SiO2 в шлаке (цифры у кривых – значения 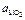 )
)
Содержание кремния в металле
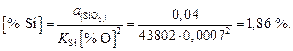
22. Расчет распределения марганца
между металлом и шлаком с использованием теории совершенных ионных растворов (ТСИР)
Задача. Рассчитать равновесное распределение марганца между металлом и шлаком при 1873 К, использовав ТСИР для оценки активности компонентов шлака.
Исходные данные. Металл – практически чистое железо. Принимаем  ,
, 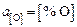 ,
, 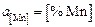 . Состав шлака тот же, что и в задаче 20, содержание железа
. Состав шлака тот же, что и в задаче 20, содержание железа 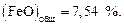
Теория. ТСИР основана на предположении, что энтальпия смешения раствора равна нулю, а парциальная энтропия смешения в выражении для химического потенциала
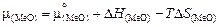 (2.5)
(2.5)
равна
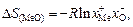 (2.6)
(2.6)
где 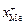 и
и 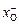 – соответственно катионная доля металла и анионная доля кислорода в шлаке. Катионная и анионная доли представляют собой соотношение числа ионов данного компонента и ионов того же знака. Эти величины получили название ионных долей по Темкину. Сопоставляя получаемое при этом выражение для химического потенциала
– соответственно катионная доля металла и анионная доля кислорода в шлаке. Катионная и анионная доли представляют собой соотношение числа ионов данного компонента и ионов того же знака. Эти величины получили название ионных долей по Темкину. Сопоставляя получаемое при этом выражение для химического потенциала
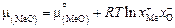 (2.7)
(2.7)
с термодинамическим определением активности
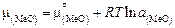 , (2.8)
, (2.8)
находим
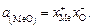 (2.9)
(2.9)
Таким образом, расчет активностей компонентов шлака по ТСИР сводится к определению ионных долей по Темкину.
При этом представляет трудность выбор вида ионов, на которые диссоциируют соединения шлака. В простейшем случае принимают, что происходит полная диссоциация на одноатомные ионы.
Решение. При условии полной диссоциации находим число молей каждого компонента (оксида) в 100 г шлака:
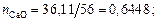
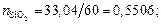
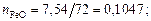
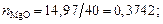
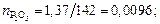
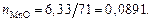
Находим суммарное число молей в 100 г шлака:
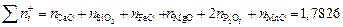 .
.
Находим ионные доли компонентов 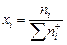 :
:
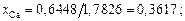
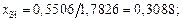
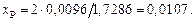
Остальные значения: 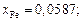
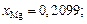
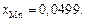 Единственным анионом в заданном шлаке является кислород
Единственным анионом в заданном шлаке является кислород 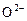 , поэтому
, поэтому 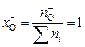 . Тогда активности оксидов в шлаке в соответствии с уравнением (2.9) равны их катионным долям. Константа реакции
. Тогда активности оксидов в шлаке в соответствии с уравнением (2.9) равны их катионным долям. Константа реакции
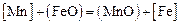
определяется по формуле [17]:
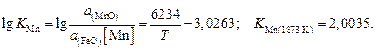
Содержание марганца в металле составляет
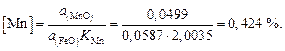
Примечание. Наилучшие результаты ТСИР дает при описании распределения серы между металлом и основным (> 30 % СаО) шлаком. В других случаях ТСИР может применяться лишь для грубых оценок активностей.
23. Расчет распределения элементов
между металлом и шлаком с использованием теории регулярных ионных растворов (ТРИР)
Задача. Рассчитать равновесное распределение марганца, кислорода и фосфора между металлом и шлаком при 1873 К, использовав ТРИР.
Исходные данные. Те же, что в задачах 20 и 22.
Теория. В регулярном ионном растворе энтропия находится как в совершенном ионном растворе (задача 22), а энтальпия – как в регулярном. Например, выражение для химического потенциала компонента бинарного раствора FeO–MnO имеет вид:
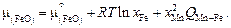 (2.10)
(2.10)
Сравнив выражение (2.10) с определением химического потенциала в виде
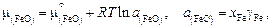
можно получить
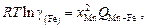 (2.11)
(2.11)
где 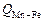 – определяемый из опыта постоянный множитель;
– определяемый из опыта постоянный множитель; 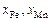 – ионные доли по Темкину (см. задачу 22).
– ионные доли по Темкину (см. задачу 22).
Выражение (2.10) было обобщено В.А. Кожеуровым для шлаков сложного состава. Полученные при этом выражения [18] для коэффициентов активности 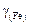 и
и 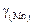 имеют вид:
имеют вид:
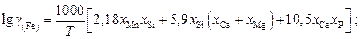 (2.12)
(2.12)
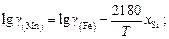 (2.13)
(2.13)
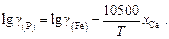 (2.14)
(2.14)
Решение. Выражаем состав шлака в ионных долях по Темкину (см. задачу 22): 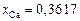 ,
, 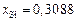 ,
, 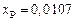 ,
, 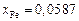 ,
, 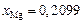 ,
, 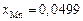 . Вычисляем коэффициенты активности:
. Вычисляем коэффициенты активности:
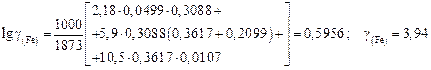 ;
;
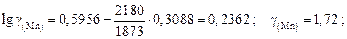
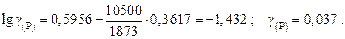
Находим активности компонентов шлака:
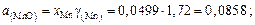
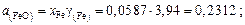
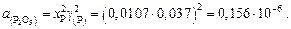
Содержание марганца найдем по равновесию реакции (для основных шлаков) 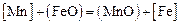 :
:
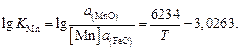
При 1873 К 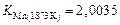 ,
,
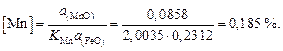
Содержание фосфора определяем по зависимости константы равновесия реакции 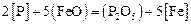 :
:
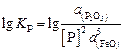
и значению константы равновесия для диапозона температур 1863–1883 К (данные [18]) 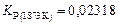
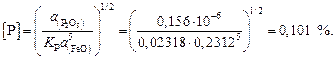
Содержание кислорода определяем по зависимости константы равновесия реакции (2.1) – 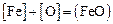 – по уравнению (2.3) [8]:
– по уравнению (2.3) [8]:
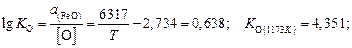
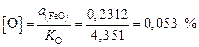 .
.
Примечание. ТРИР относится к числу наиболее совершенных методов оценки активностей компонентов шлаковых систем. Основная трудность применения теории заключается в отсутствии надежных данных об энергиях смешения для ряда практически важных шлаков, в частности шлаков, содержащих Аl2O3 и СаF2 .
24. Активность компонентов шлака как фазы
с коллективизированными электронами
Задача. Рассчитать распределение марганца между металлом и шлаком, использовав методику оценки термодинамических функций шлака как фазы с коллективизированными электронами (КЭ) [3].
Исходные данные. Те же, что в задаче 20.
Теория. Известно, что в оксидах, как и в металлах, электроны всех атомов, образующих фазу, составляют единую квантово-механическую систему, которую термодинамически можно характеризовать химическим потенциалом электронов (уровнем Ферми). Это позволяет парциальную энтропию смешения 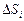 представить в виде двух составляющих, учитывающих тепловое возбуждение ядер и электронов отдельно:
представить в виде двух составляющих, учитывающих тепловое возбуждение ядер и электронов отдельно: 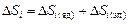 . Слагаемое
. Слагаемое 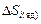 , как и обычно в теории растворов, учитывает лишь составляющую теплового движения, связанную с обменом местами (перестановками) между различными ядрами (атомами),
, как и обычно в теории растворов, учитывает лишь составляющую теплового движения, связанную с обменом местами (перестановками) между различными ядрами (атомами), 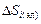 учитывает тепловое возбуждение электронов – перевод некоторой их части из валентной зоны в зону проводимости. В простейшем варианте этого метода, как и в ТРИР (и ТСИР), парциальная энтальпия смешения
учитывает тепловое возбуждение электронов – перевод некоторой их части из валентной зоны в зону проводимости. В простейшем варианте этого метода, как и в ТРИР (и ТСИР), парциальная энтальпия смешения 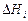 считается равной нулю. При этом выражение для химического потенциала элемента i в шлаке имеет вид:
считается равной нулю. При этом выражение для химического потенциала элемента i в шлаке имеет вид:
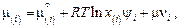 (2.15)
(2.15)
где 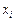 – концентрация элемента
– концентрация элемента 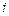 в шлаке в атомных долях;
в шлаке в атомных долях; 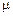 (без индекса) – химический потенциал электронов в шлаковой фазе;
(без индекса) – химический потенциал электронов в шлаковой фазе; 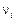 – валентность (степень окисления) элемента
– валентность (степень окисления) элемента 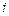 в шлаке. В равновесии с металлом
в шлаке. В равновесии с металлом 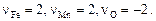 Коэффициент активности
Коэффициент активности 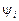 является частью «обычного» коэффициента активности
является частью «обычного» коэффициента активности 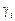 :
:
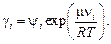 (2.16)
(2.16)
Коэффициент активности 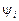 вычисляется по формуле
вычисляется по формуле
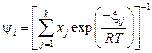 , (2.17)
, (2.17)
где 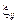 – энергия обмена местами атомов i и j, которая оценивается по формуле
– энергия обмена местами атомов i и j, которая оценивается по формуле
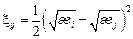 , (2.18)
, (2.18)
где 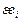 ,
, 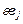 – энергетические параметры элементов i и j [3], кДж, равные
– энергетические параметры элементов i и j [3], кДж, равные
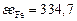
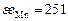
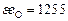
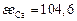
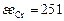
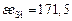
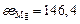
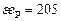
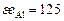
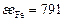
Соотношения (2.15) – (2.18) позволяют выразить химический потенциал компонента 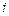 как функцию состава фазы. На основании условия химического равновесия
как функцию состава фазы. На основании условия химического равновесия 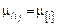 , принимая для металла выражение
, принимая для металла выражение 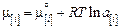 , получаем выражение для константы
, получаем выражение для константы
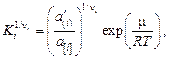 (2.19)
(2.19)
где 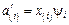 .
.
Для исключения 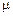 разделим полученное выражение на аналогичное, записанное для любого другого компонента
разделим полученное выражение на аналогичное, записанное для любого другого компонента 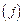 шлака:
шлака:
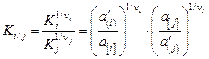 . (2.20)
. (2.20)
Это выражение эквивалентно закону действующих масс для реакции
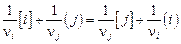 (2.21)
(2.21)
или применительно к данной задаче
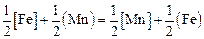 . (2.22)
. (2.22)
Для последней реакции константа равновесия равна константе равновесия реакции обмена, записанной в обычной форме через оксиды:
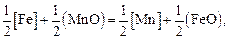 (2.23)
(2.23)
т.е. 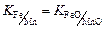 .
.
Решение. Компонентами как металлической, так и шлаковой фаз в этом методе считаются химические элементы. Их концентрации в обеих фазах выражаются в атомных долях.
I. Определяем состав заданного шлака в атомных долях.
1. Находим число молей каждого оксида в 100 г шлака:
nСаO = 36,11/56 = 0,6448; nSiO2 = 33,04/60 = 0,5506;
nFeO = 6,41/72 = 0,0890; nFe2O3 = 1,26/160 = 0,0078;
nMgO = 14,97/40 = 0,3742; nP2O5 = 1,37/142 = 0,0096;
nMnO = 6,33/71 = 0,0891.
2. Находим число молей элементов масс элементов в 100 г шлака:
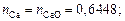
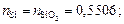
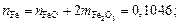
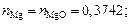
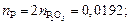
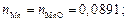
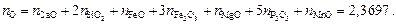
3. Находим сумму чисел молей всех компонентов:
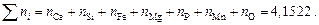
4. Вычисляем атомные доли компонентов шлака 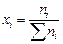 :
:
xСа = 0,6448/4,1522 = 0,1552; хSi = 0,5506/4,1522 = 0,1326;
xFe = 0,1046/4,1522 = 0,0251; xMg = 0,3742/4,1522 = 0,0901;
xP = 0,0192/4,1522 = 0,0046; xMn = 0,0891/4,1522 = 0,0214 ;
xO = 2,3697/4,1522 = 0,5707.
II. Коэффициенты активности марганца и железа 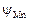 и
и 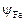 вычисляем по формуле (2.17). Для этого сначала вычислим по формуле (2.18) обменные энергии железа и марганца со всеми компонентами шлака
вычисляем по формуле (2.17). Для этого сначала вычислим по формуле (2.18) обменные энергии железа и марганца со всеми компонентами шлака 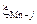 и
и 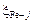 . Например,
. Например,
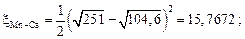
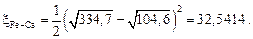
Затем найдем множитель 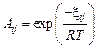 , например, для
, например, для 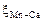 и
и 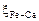
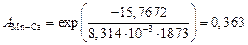 ;
;
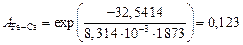 .
.
Результаты вычислений приведены ниже:
| Ca | Si | Fe | Mg | P | Mn | O | |
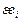 , кДж , кДж
| 104,6 | 171,5 | 334,7 | 146,4 | 205 | 251 | 1255 |
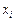
| 0,1552 | 0,1326 | 0,0251 | 0,0901 | 0,0046 | 0,0214 | 0,5707 |
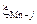 , кДж , кДж
| 15,76 | 3,77 | 3,00 | 7,00 | 1,16 | 0 | 191,7 |
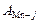
| 0,363 | 0,787 | 0,824 | 0,637 | 0,928 | 1 | 0 |
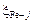 , кДж , кДж
| 32,54 | 13,51 | 0 | 19,19 | 7,91 | 3,00 | 146,7 |
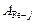
| 0,123 | 0,419 | 1 | 0,291 | 0,601 | 0,824 | 0 |
Вычисляем коэффициенты активности
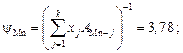
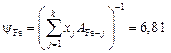
и активности компонентов 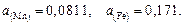
III. По равновесию реакции обмена 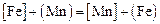 , идентичной реакции
, идентичной реакции 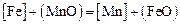 , для которой при 1873 К значение константы равновесия равно обратному значению константы, определенной в задачах 20, 22
, для которой при 1873 К значение константы равновесия равно обратному значению константы, определенной в задачах 20, 22 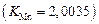 ,
,
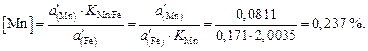
По равновесию реакции 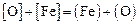 , идентичной реакции
, идентичной реакции 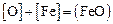 , имеющей константу равновесия, определяемую по уравнению
, имеющей константу равновесия, определяемую по уравнению
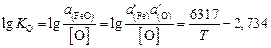 , (2.24)
, (2.24)
при 1873 К 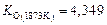 .
.
Поскольку 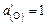 , определяем содержание кислорода в металле [О] по уравнению
, определяем содержание кислорода в металле [О] по уравнению 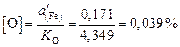 .
.
Примечание. Основным достоинством метода является полная обеспеченность численными параметрами, что позволяет делать оценки активностей в шлаках любого состава. По точности оценок этот метод близок к ТРИР.
25. Активность компонентов кислого шлака
Задача. Рассчитать активность кремнезема в шлаке системы 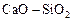 с использованием модели коллективизированных электронов.
с использованием модели коллективизированных электронов.








