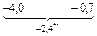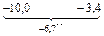2. Термодинамический метод часто используется для построения диаграммы состояния.
3. Область применения ТРР ограничена системами, образующими непрерывный ряд твердых растворов. В общем случае описанный метод расчета термодинамических величин является приближенным и может быть рекомендован только для оценочных расчетов при отсутствии экспериментальных данных.
15. Расчет теплот образования сплавов
по данным об атомных параметрах компонентов (по методу Миедемы)
Задача. Рассчитать теплоту растворения кальция в жидком железе по данным об атомных параметрах кальция и железа: электроотрицательности, объеме, электронной плотности и энергии р-, d-гибридизации.
Исходные данные. 1. Электроотрицательность k, объем V2/3, электронная плотность n1/3 железа и кальция [14]:
| Fe | Ca | |
| k, еB | 4,93 | 2,55 |
| V 2/3, (см3/моль)2/3 | 3,69 | 8,82 |
| n1/3 | 1,77 | 0,91 |
2. Параметр R, характеризующий энергию гибридизации между р-состояниями кальция и d-состояниями железа, R = 0,40.
Теория. В описании термодинамических свойств металлических расплавов важную роль играют размерный и электрохимический факторы. Размерный фактор, характеризующий различие в атомных размерах компонентов сплава, обусловливает положительный вклад в теплоту образования сплава DH. Электрохимический фактор, связанный с различием электроотрицательностей компонентов, дает отрицательный вклад в величину DH. Метод Миедемы [14] развивает известную схему расчета термодинамических характеристик сплавов, основанную на учете электрохимического и размерного факторов. В методе Миедемы металл разделяют на электронейтральные элементарные ячейки Вигнера – Зейтца, характеризующиеся распределением электронной плотности, которая различна для разных металлов. При образовании сплава происходит выравнивание химических потенциалов электрона в разнородных ячейках и электронной плотности на границах разнородных ячеек. Первый процесс протекает в результате переноса электронного заряда, что приводит к отрицательному вкладу в энергию образования сплава. Величина этого вклада DH1 пропорциональна квадрату разности электроотрицательностей компонентов: DH1 » -(k1 - k2)2. Второй процесс, связанный с деформацией ячеек Вигнера – Зейтца, требует затраты энергии:
DH2 » 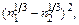 где п i - плотность электронов на границе ячейки Вигнера – Зейтца у компонента i. Метод Миедемы является полуэмпирическим. Значения ki определяют по данным о работе выхода электрона, а величины п i являются параметрами теории, они устанавливаются эмпирически, путем анализа массива данных о теплотах образования интерметаллических соединений и расплавов. Уравнение Миедемы для расчета теплот образования сплавов имеет вид:
где п i - плотность электронов на границе ячейки Вигнера – Зейтца у компонента i. Метод Миедемы является полуэмпирическим. Значения ki определяют по данным о работе выхода электрона, а величины п i являются параметрами теории, они устанавливаются эмпирически, путем анализа массива данных о теплотах образования интерметаллических соединений и расплавов. Уравнение Миедемы для расчета теплот образования сплавов имеет вид:
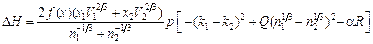 , (1,51)
, (1,51)
где функция f (x) для жидких сплавов равна: 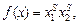
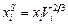 ´ ´
´ ´ 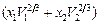 - поверхностная мольная концентрация компонента i. Вклад R учитывает эффекты гибридизации р-и d-состояний, коэффициент a для расплавов равен 0,73. Параметр р принимают равным 12,3 кДж/моль для сплавов, образованных переходными металлами с простыми, и 14,2 кДж/моль, если оба компонента - переходные металлы или один из них переходный, другой - благородный (Аg, Cu, Au). Коэффициент Q равен 9,4. Для расчета парциальных теплот растворения компонентов следует воспользоваться уравнением Гиббса – Дюгема. Уравнение для расчета начальной теплоты растворения компонента 2 в жидком металле 1 имеет вид:
- поверхностная мольная концентрация компонента i. Вклад R учитывает эффекты гибридизации р-и d-состояний, коэффициент a для расплавов равен 0,73. Параметр р принимают равным 12,3 кДж/моль для сплавов, образованных переходными металлами с простыми, и 14,2 кДж/моль, если оба компонента - переходные металлы или один из них переходный, другой - благородный (Аg, Cu, Au). Коэффициент Q равен 9,4. Для расчета парциальных теплот растворения компонентов следует воспользоваться уравнением Гиббса – Дюгема. Уравнение для расчета начальной теплоты растворения компонента 2 в жидком металле 1 имеет вид:
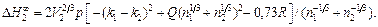 (1.52)
(1.52)
Решение. Кальций относится к простым металлам, поэтому значение параметра р следует принять равным 12,3 кДж/моль. Подставив исходные данные в уравнение (1.52), получим
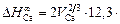
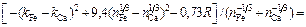
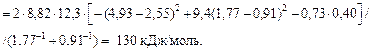
Примечания. 1. Рассчитанное значение 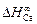 хорошо согласуется с экспериментальной величиной, равной 121 кДж/моль, найденной по растворимости кальция в жидком железе.
хорошо согласуется с экспериментальной величиной, равной 121 кДж/моль, найденной по растворимости кальция в жидком железе.
2. Для упорядоченной фазы (например, химические соединения) функцию f (х) в уравнении (1.51) следует рассчитывать по уравнению f(х) = 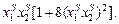 Для твердых сплавов коэффициент a при параметре р-, d-гибридизации R принимают равным 1.
Для твердых сплавов коэффициент a при параметре р-, d-гибридизации R принимают равным 1.
3. Объемы компонентов, использованные в расчете DH, соответствуют твердому состоянию. Например, для жидкого железа при Тпл , величина V 2/3 равна 4,0 (см3/моль)2/3, а не 3,69. В данном случае величину 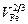 = 3,69, как и другие значения V 2/3, рекомендованные в работе [14] для расчета DH для расплавов, следует рассматривать как параметры теории.
= 3,69, как и другие значения V 2/3, рекомендованные в работе [14] для расчета DH для расплавов, следует рассматривать как параметры теории.
4. Метод Миедемы в общем случае является приближенным. Например, рассчитанные этим методом начальные теплоты растворения кремния и алюминия в жидком железе равны -76 и -50 кДж/моль, в то время как экспериментальные значения составляют -132 и -63 кДж/моль соответственно. Метод Миедемы можно рекомендовать как оценочный в тех случаях, когда отсутствуют экспериментальные термодинамические данные.
16. Графическое определение параметров взаимодействия
Задача. Графически определить параметры взаимодействия 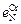 и
и 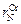 в жидком никеле при 1873 К по данным о растворимости азота в сплавах Ni–Cr.
в жидком никеле при 1873 К по данным о растворимости азота в сплавах Ni–Cr.
Исходные данные. В расплавах Ni–Cr экспериментально определены [15] значения растворимости азота [N] при 1873 К и рN2 = 1 атм в зависимости от концентрации хрома:
| [Cr], % | 0 | 2,93 | 10 | 20 | 30 |
| [N], % | 0,0015 | 0,0031 | 0,0105 | 0,062 | 0,180 |
Теория. Параметры взаимодействия являются коэффициентами ряда Тейлора, в который можно разложить логарифм коэффициента активности компонента раствора (lg fi) вблизи точки, соответствующей чистому растворителю [3]. Для рассматриваемых сплавов имеем
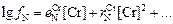 (1.53)
(1.53)
В этой формуле 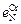 и
и 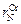 являются параметрами взаимодействия первого и второго порядков:
являются параметрами взаимодействия первого и второго порядков:
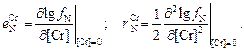 (1.54)
(1.54)
Если имеется график зависимости lgfN от [% Cr], то параметр 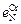 можно найти как тангенс угла наклона касательной к кривой в точке с абсциссой [% Cr] = 0;
можно найти как тангенс угла наклона касательной к кривой в точке с абсциссой [% Cr] = 0; 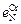 = tg a½[Cr] = 0 . Далее, найдя аналогичным образом значение tg a¢ в точке, соответствующей некоторому другому значению [% Cr], можно определить параметр
= tg a½[Cr] = 0 . Далее, найдя аналогичным образом значение tg a¢ в точке, соответствующей некоторому другому значению [% Cr], можно определить параметр 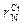 как изменение тангенса угла наклона касательной, отнесенное к изменению [% Cr]:
как изменение тангенса угла наклона касательной, отнесенное к изменению [% Cr]:
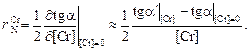 (1.55)
(1.55)
Чтобы найти значения lg fN по имеющимся данным о растворимостях [N], учтем, что все они относятся к одному давлению азота в газовой фазе. Отсюда следует, что активности азота во всех расплавах одинаковы: aN = fN[N] = const. При [Cr] = 0 коэффициент активности азота равен 1, так как fN в данном случае учитывает влияние хрома на aN. Отсюда aN = [N][Cr] = 0 и, следовательно,
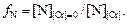 (1.56)
(1.56)
Решение. Найдем с помощью выражения (1.56) коэффициенты активности азота в заданных сплавах и их логарифмы:
| [Cr], % | 0 | 2,93 | 10 | 20 | 30 |
| fN | 1 | 0,484 | 0,143 | 0,024 | 0,0083 |
| lg fN | 0 | -0,315 | -0,845 | -1,616 | -0,079 |
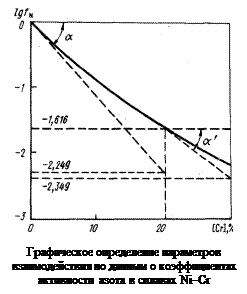
Построим график зависимости lg fN от [% Cr] (см. рисунок). Проведем касательные к полученной кривой в точках, соответствующих содержанию хрома 0 и 20 %. Определим графически ординаты точек пересечения касательных с вертикалями 20 и 30 % Cr (эти ординаты показаны на рисунке). В результате получим
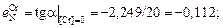
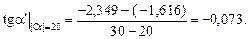
В соответствии с уравнением (1.55)
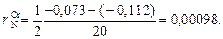
 Примечание. При использовании ЭВМ параметры взаимодействия
Примечание. При использовании ЭВМ параметры взаимодействия 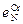 и
и 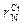 можно найти как коэффициенты полинома второго порядка, аппроксимирующего зависимость коэффициента активности азота (lg fN) от содержания хрома [Cr]. Обычно при этом оценивают также погрешность (доверительный интервал) определяемых параметров. Если экспериментальные данные относятся к различным температурам, то находят параметры в виде их температурных зависимостей типа
можно найти как коэффициенты полинома второго порядка, аппроксимирующего зависимость коэффициента активности азота (lg fN) от содержания хрома [Cr]. Обычно при этом оценивают также погрешность (доверительный интервал) определяемых параметров. Если экспериментальные данные относятся к различным температурам, то находят параметры в виде их температурных зависимостей типа
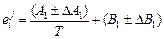 ;
;
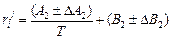 .
.
17. Оценка параметров взаимодействия
по известным значениям этих параметров
для элементов-аналогов, связь между 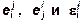
Задача. Определить приблизительные значения параметра 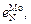 пользуясь методом сравнения с известными значениями параметров для элементов-аналогов молибдена или азота.
пользуясь методом сравнения с известными значениями параметров для элементов-аналогов молибдена или азота.
Теория. В таблицах параметров взаимодействия (табл. П3) довольно много отсутствующих значений. Для сплавов на нежелезной основе (например, для никелевых) количество известных параметров намного меньше. При оценке коэффициентов активности отсутствующие параметры взаимодействия часто принимают равными нулю. Это может приводить к большим неточностям. Более правильно в этих случаях попытаться хотя бы очень грубо оценить неизвестные значения параметров, пользуясь известными значениями их для элементов-аналогов1. Аналогами можно считать элементы, находящиеся в одной группе Периодической системы элементов Д.И. Менделеева. При отсутствии данных для прямых аналогов можно воспользоваться более далекими аналогами-элементами соседних групп в том же периоде (или в соседних периодах). Переходные и непереходные элементы следует рассматривать отдельно. В первом приближении можно принять, что значения параметров представляют собой средние арифметические по отношению к параметрам для элементов-аналогов. Усреднение лучше проводить для параметров 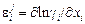 , а не
, а не 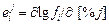 , так как параметры
, так как параметры 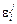 связаны с количеством (а не с массой) атомов.
связаны с количеством (а не с массой) атомов.
Связь между параметрами определяется соотношениями [3]
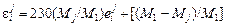 *; (1.57)
*; (1.57)
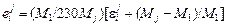 *; (1.58)
*; (1.58)
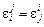 . (1.59)
. (1.59)
Сравнительные данные можно выбирать как для аналогов элемента i, так и для аналогов j.
Решение. При оценке параметра 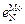 можно воспользоваться двумя парами известных значений параметров для элементов-аналогов:
можно воспользоваться двумя парами известных значений параметров для элементов-аналогов: 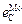 –
– 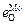 и
и 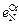 –
– 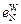 . Табличные значения
. Табличные значения 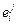 (табл. П3), а также результаты расчетов параметров
(табл. П3), а также результаты расчетов параметров 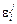 по уравнению (1.57) и путем усреднения приведены ниже:
по уравнению (1.57) и путем усреднения приведены ниже:
| j/i | Мо/С | Мо/О | Сr/N | W/N |
| М j | 96 | 96 | 52 | 184 |
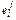
| -0,0083 | 0,0035 | 0,047 | -0,0015 |
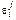
|
|
| ||
|
| ||||
|
| ||||
В действительности (табл. П3) параметр 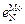 = -0,011 и, следовательно,
= -0,011 и, следовательно,
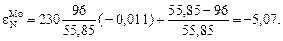
Это значение близко к полученной выше итоговой оценке 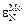 = -4,55. Такая точность достигается далеко не всегда. Однако при использовании для расчета параметра
= -4,55. Такая точность достигается далеко не всегда. Однако при использовании для расчета параметра 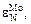 равного -2,4 или -6,7, ошибка была бы тоже меньше, чем при использовании параметра равного нулю.
равного -2,4 или -6,7, ошибка была бы тоже меньше, чем при использовании параметра равного нулю.
Параметр 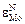 , согласно уравнению (1.59), равен
, согласно уравнению (1.59), равен 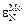 .
.
18. Теоретическая оценка параметра 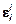
по значениям коэффициента активности gi
и параметра 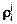 по
по 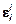
Задача. Зная коэффициент активности компонента gi , определить параметры взаимодействия 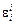 и
и 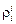 при 1873 К с помощью ТРР.
при 1873 К с помощью ТРР.
Исходные данные. Коэффициент активности меди в железе 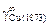 = 8,6 [3].
= 8,6 [3].
Теория. Как показано в работе [3], концентрационная и температурная зависимость gi выражается в ТРР уравнением
ln gi (T ) = (W/RT )(1 - xi)2, (1.60)
где W - энергия смешения, в простейшем варианте ТРР не зависящая ни от температуры, ни от концентрации. Дифференцируя уравнение (1.60) по х i и принимая х i ® 0, получаем
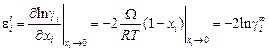 ; (1.61)
; (1.61)
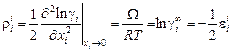 . (1.62)
. (1.62)
Решение. Для системы Fe–Cu
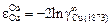 = -2 × 2,303 × 0,9345 = -4,3;
= -2 × 2,303 × 0,9345 = -4,3;
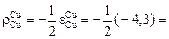 2,15.
2,15.
Примечание. В ТКР концентрационная и температурная зависимость gi определяется выражением [3]:
ln gi(T) = (W/RT )(1 – T/t)(1 - xi)2, (1.63)
где t = 7000 - параметр ТКР, определенный по экспериментальным данным. Как видно из выражения (1.63), концентрационные зависимости gi в ТРР и ТКР одинаковы. Следовательно, выражения (1.61) и (1.62) справедливы для обеих теорий.
19. Зависимость параметров взаимодействия
от температуры