3. По данным о приведенных энергиях Гиббса [9] находим
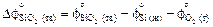 = 100,28 - 46,06 - 236,92 =
= 100,28 - 46,06 - 236,92 =
= -182,7 Дж/(К×моль);
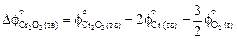 = 192,82 -
= 192,82 -
- 2×51,86 - 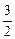 ×236,92 = -266,28 Дж/(К×моль).
×236,92 = -266,28 Дж/(К×моль).
Используя уравнение (1.37) и исходные данные о теплотах образования оксидов при 0 К, получаем
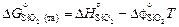 = -905717 + 182,7×1873 =
= -905717 + 182,7×1873 =
= -563520 Дж/моль;
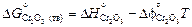 = -1134777 + 266,28×1873 =
= -1134777 + 266,28×1873 =
= -636035 Дж/моль.
Стандартная энергия Гиббса реакции восстановления хрома кремнием [уравнение (1.34)]
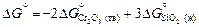 .
.
Подстановка найденных по разным данным значений 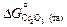 и
и 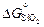 дает следующие результаты:
дает следующие результаты:
1) DG° = 2×651079 - 3×542070 = -324052 Дж/моль; K = 9,8×1010 ;
2) DG° = 2×662750 - 3×576146 = -402938 Дж/моль; K = 1,73×1011 ;
3) DG° = 2×636035 - 3×563520 = -418490 Дж/моль; K = 2,10×1012 .
Примечания. 1. Рассчитанные разными способами значения DGo заметно различаются. Это связано с точностью определения величин 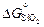 и
и 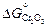 . По данным [8] при комнатной температуре она составляет ~ 2 кДж/моль для Сr2O3 и ~ 4 кДж/моль для SiO2. Более точными являются значения DG°, рассчитанные по данным [9] о приведенных потенциалах.
. По данным [8] при комнатной температуре она составляет ~ 2 кДж/моль для Сr2O3 и ~ 4 кДж/моль для SiO2. Более точными являются значения DG°, рассчитанные по данным [9] о приведенных потенциалах.
2. В некоторых справочных таблицах даны приведенные потенциалы веществ не при 0 К, а при 298 К. В этом случае
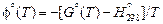 ,
,
где 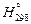 - энтальпия вещества при 298 К.
- энтальпия вещества при 298 К.
11. Расчет термодинамических свойств бинарных расплавов в приближении
теории регулярных растворов (ТРР)
Задача. В приближении ТРР рассчитать коэффициенты активности ванадия и железа, парциальные и интегральные энтальпии, энтропии и энергии Гиббса расплавов Fe–V по данным о начальной теплоте растворения ванадия в железе.
Исходные данные. Начальная теплота растворения ванадия в жидком железе при 1873 К: 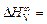 -48073 Дж/моль [10] (стандартное состояние – жидкий ванадий).
-48073 Дж/моль [10] (стандартное состояние – жидкий ванадий).
Теория. В ТРР предполагается, что отклонение раствора от совершенного обусловлено только энтальпийным членом (DHm ¹ 0), а энтропия регулярного раствора такая же, как совершенного ( 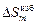 = 0), т.е. предполагается, что расположение атомов хаотично, как в идеальном растворе. Энтропия образования бинарного регулярного раствора
= 0), т.е. предполагается, что расположение атомов хаотично, как в идеальном растворе. Энтропия образования бинарного регулярного раствора
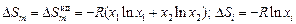 .
.
В ТРР энтальпия определяется уравнениями
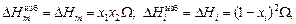 (1.38)
(1.38)
где W - энергия взаимообмена (смешения), является параметром теории
W = -zNA [e1, 2 -  (e1, 1 + e2, 2)];
(e1, 1 + e2, 2)];
N A - число Авогадро; ei, j - энергия взаимодействия между атомами i и j, расположенными в соседних узлах квазирешетки с координационным числом z.
Энергия Гиббса в ТРР равна
DGm = DHm – TDSm = х1x2W + RТ(x1lnх1 + x2lnх2);
DGi = DHi – TDSi = (1 - х i)2W + RТ lnх i ;
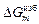 = DHm = х1x2W;
= DHm = х1x2W;
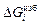 = RT lngi = DHi = (1 – х i)2W.
= RT lngi = DHi = (1 – х i)2W.
Отсюда
lngi = (1 – х i)2W/RТ. (1.39)
Таким образом, для расчета термодинамических характеристик бинарного расплава в приближении ТРР необходимо знать параметр W. Как правило, его определяют по экспериментальным данным, используя уравнения (1.38) или (1.39).
Решение. Для определения энергии взаимообмена в расплаве Fе–V воспользуемся исходными данными о величине 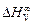 . В соответствии с уравнением (1.38) имеем: W =
. В соответствии с уравнением (1.38) имеем: W = 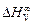 = -48073 Дж/моль. Рассчитаем термодинамические свойства расплава, содержащего 10 % ат. V (xV = 0,1), при 1873 К:
= -48073 Дж/моль. Рассчитаем термодинамические свойства расплава, содержащего 10 % ат. V (xV = 0,1), при 1873 К:
DHm = xFexVW = -0,9×0,1×48073 = -4326 Дж/моль;
DHV = (1 - xV)2W = -(1 - 0,1)2×48073 = -38939 Дж/моль;
DHFe = (1 - xFe)2W = -(1 - 0,9)2×48073 = -481 Дж/моль;
lngV =DHV/RT = -38393/(8,314×1873) = -2,50; gV = 0,082;
lngFe = DHFe/RT = -481/(8,314×1873) = -0,031; gFe = 0,970;
DSm = -R(xVlnxV + xFelnxFe) = -8,314 (0,1 ln0,1 + 0,9ln0,9) =
= 2,70 Дж/(моль×К);
DSV = -RlnxV = -8,314 ln0,1 = 19,147 Дж/(моль×К) ;
DSFe = -RlnxFe = -8,314 ln0,9 = 0,876 Дж/(моль×К);
DGm = DHm - TDSm = 4326 - 1873×2,70 = -9402 Дж/моль;
DGV = DHV - TDSV = -38939 - 1873×19,15 = -74804 Дж/моль;
DGFe = DHFe - TDSFe = -481 - 1873×0,88 = -2129 Дж/моль.
Результаты расчета концентрационных зависимостей термодинамических свойств расплава Fе–V в сопоставлении с экспериментальными данными [10] приведены в таблице.
Результаты расчета термодинамических свойств расплавов Fе–V при 1873 К
в приближении ТРР (числитель) и экспериментальные данные [10] (знаменатель)
| Термодинамическая характеристика | Значение термодинамической характеристики1 при разных хV | ||||||||
| 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | |
| -DHm | 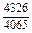
| 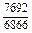
| 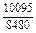
| 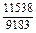
| 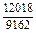
| 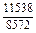
| 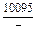
| 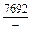
| 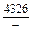
|
| -DHV | 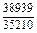
| 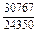
| 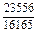
| 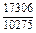
| 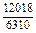
| 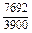
| 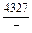
| 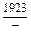
| 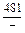
|
| -DHFe | 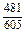
| 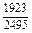
| 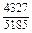
| 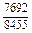
| 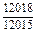
| 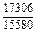
| 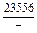
| 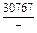
| 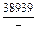
|
| gV | 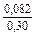
| 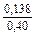
| 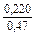
| 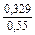
| 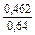
| 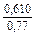
| 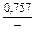
| 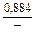
| 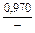
|
| gFe | 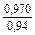
| 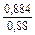
| 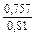
| 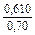
| 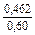
| 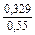
| 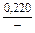
| 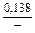
| 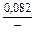
|
| DSm | 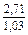
| 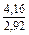
| 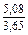
| 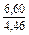
| 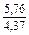
| 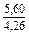
| 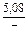
| 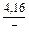
| 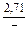
|
| DSV | 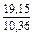
| 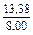
| 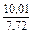
| 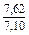
| 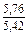
| 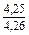
| 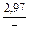
| 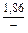
| 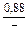
|
| DSFe | 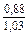
| 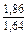
| 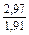
| 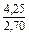
| 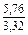
| 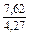
| 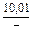
| 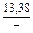
| 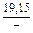
|
| -DGm | 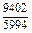
| 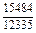
| 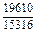
| 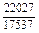
| 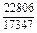
| 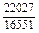
| 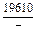
| 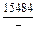
| 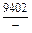
|
| -DGV | 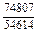
| 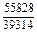
| 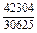
| 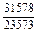
| 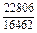
| 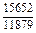
| 
| 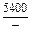
| 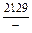
|
| -DGFe | 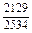
| 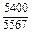
| 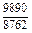
| 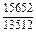
| 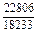
| 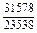
| 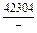
| 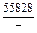
| 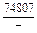
|
| _______________ 1 DH, DG, Дж/моль; DS, Дж/(моль×К). | |||||||||
Примечания. 1. Термин «регулярные растворы» не связан с существом модели [3]. Он введен Гильдебрандом для обозначения семейства растворов, характеризующихся определенной закономерностью (регулярностью) изменения ряда свойств. Оказалось, что рассмотренная модель удовлетворительно описывает свойства таких растворов. В результате и сама модель получила название регулярного раствора.
2. Величина параметра W в ТРР может быть определена различными способами: по известной экспериментальной теплоте образования расплава, по данным об энергии Гиббса расплава или коэффициенте активности одного из компонентов. Значения W, рассчитанные с помощью различных термодинамических величин, могут заметно различаться. Так, при определении W по экспериментальной теплоте образования расплава эквиатомного состава (xV = xFe = 0,5) DHm = -9162 Дж/моль, получим W = -36648 Дж/моль. Расчет W по значениям коэффициента активности ванадия при xV = 0,5, gV = 0,64 дает W = -6942 Дж/моль. Различие результатов расчета является следствием отклонения системы Fe–V от регулярных растворов.
3. В приближении ТРР кривые, описывающие термодинамические свойства бинарных расплавов в зависимости от состава, симметричны относительно точки х1 = x2 = 0,5. Экспериментальные концентрационные зависимости, как правило, асимметричны. Так, для расплавов Fe–V максимум термодинамических характеристик (их абсолютных величин) соответствует хV » 0,45. Асимметрия концентрационных зависимостей свойств учитывается в теории субрегулярных растворов (ТСР) [3]. В приближении ТСР предполагается, что энергия взаимообмена линейно зависит от состава: W = х1А1 + х2А2 , где А1 и A2 - параметры, определяемые по экспериментальным значениям теплот растворения или коэффициентов активности компонентов. Для их определения требуются две экспериментальные точки. В частности, значения А1 и А2 можно найти по данным о начальных теплотах растворения: А1 = 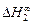 , A2 =
, A2 = 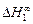 или коэффициентах активности А1 = = RТ ln
или коэффициентах активности А1 = = RТ ln 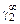 , А2 = RТ ln
, А2 = RТ ln 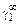 .
.
4. ТРР можно применять для систем с относительно слабым межатомным взаимодействием (например, Fe–Cr, Fe–Со, Ni–Со). Однако ТРР часто используют и для расплавов с сильным межатомным взаимодействием. Например в тех случаях, когда экспериментальные данные ограничены, так что можно рассчитать только один параметр W.
12. Расчет термодинамических свойств бинарных расплавов в приближении теории квазирегулярных растворов (ТКР)
Задача. В приближении ТКР рассчитать концентрационные зависимости избыточных парциальных и интегральных значений энергии Гиббса, энтальпии и энтропии по известному коэффициенту активности титана в разбавленном растворе железа при 1873 К.
Исходные данные. Коэффициент активности титана в разбавленном растворе железа при 1873 К: 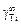 = 0,037 (стандартное состояние - жидкий титан).
= 0,037 (стандартное состояние - жидкий титан).
Теория. В ТКР конфигурационную составляющую энтропии принимают равной энтропии идеального раствора, а неконфигурационную (колебательную) - пропорциональной теплоте образования раствора. Таким образом, избыточная интегральная энтропия в ТКР
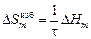 ,
,
где t - параметр, равный по данным [3] для расплавов на основе железа и никеля 7000 К.
Как и в ТРР, теплота образования раствора в ТКР определяется уравнением DHm = х1x2W. Избыточная интегральная энергия Гиббса
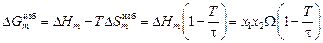 .
.
Уравнения для расчета избыточных парциальных термодинамических величин в ТКР имеют вид:
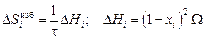 ; (1.40)
; (1.40)
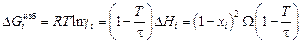 . (1.41)
. (1.41)
Таким образом, для расчета термодинамических характеристик бинарного расплава в приближении ТКР должны быть известны два параметра: t и W. Величину t для расплавов на основе железа и никеля можно принять равной 7000 К. Она определена в работе [3] на основе обобщения и анализа известных данных о теплотах растворения и коэффициентах активности элементов в жидких железе и никеле. Величину W можно найти по уравнениям (1.40) или (1.41), использовав экспериментальные значения DHi или gi .
Решение. Энергию взаимообмена W для расплава Fе–Тi определяем с помощью уравнения (1.41), используя заданное значение 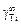 при 1873 К. Из уравнения (1.41) следует:
при 1873 К. Из уравнения (1.41) следует:
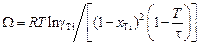 .
.
При хTi ® 0 и t = 7000 К получим
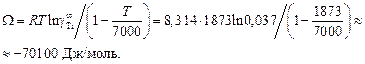
Вычисляем избыточные термодинамические характеристики расплава Fе–Тi с атомным содержанием титана 10 % (хTi = 0,1):
DHm = хFexTiW = -0,9×0,1×70100 = -6310 Дж/моль ;
DHFe = (1 - хFe)2W = -(1 - 0,9)2×70100 = -701 Дж/моль;
DHTi = (1 - хTi)2W = -(1 - 0,1)2×70100 = -56781 Дж/моль;
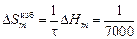 (-6310) = -0,90 Дж/(моль×К) ;
(-6310) = -0,90 Дж/(моль×К) ;
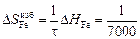 (-701) = -0,10 Дж/(моль×К) ;
(-701) = -0,10 Дж/(моль×К) ;
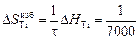 (-56780) = -8,11 Дж/(моль×К) ;
(-56780) = -8,11 Дж/(моль×К) ;
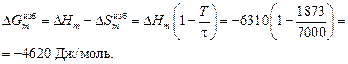
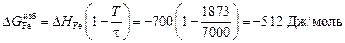 ;
;
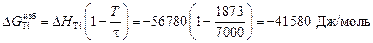 .
.
Результаты расчета концентрационных зависимостей избыточных термодинамических характеристик системы Fе–Тi при 1873 К в сопоставлении с экспериментальными данными [11] приведены в таблице.
Результаты расчета термодинамических свойств расплавов Fе–Тi при 1873 К
в приближении ТКР (числитель) и экспериментальные данные (знаменатель)
| Термодинамическая характеристика | Значение термодинамической характеристики1 при разных хTi | ||||||||
| 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | |
| -DHm | 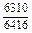
| 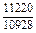
| 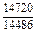
| 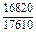
| 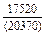
| 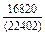
| 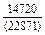
| 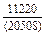
| 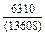
|
| -DHTi | 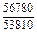
| 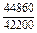
| 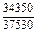
| 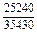
| 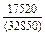
| 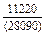
| 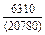
| 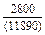
| 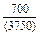
|
| -DHFe | 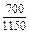
| 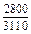
| 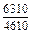
| 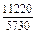
| 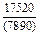
| 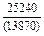
| 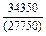
| 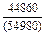
| 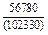
|
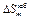
| 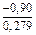
| 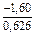
| 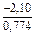
| 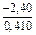
| 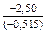
| 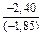
| 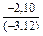
| 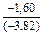
| 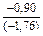
|
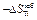
| 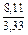
| 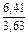
| 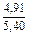
| 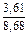
| 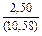
| 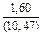
| 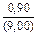
| 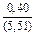
| 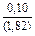
|
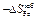
| 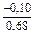
| 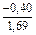
| 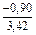
| 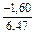
| 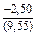
| 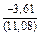
| 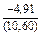
| 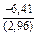
| 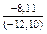
|
| 
| 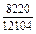
| 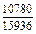
| 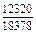
| 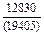
| 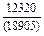
| 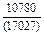
| 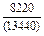
| 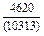
|
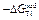
| 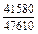
| 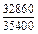
| 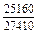
| 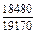
| 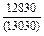
| 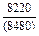
| 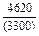
| 
| 
|
| 
| 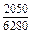
| 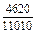
| 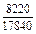
| 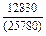
| 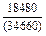
| 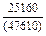
| 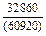
| 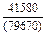
|
| ____________ 1 DH, DGизб, Дж/моль; DSизб, Дж/(моль×К). | |||||||||
Примечания. 1. В приближении ТКР, как и ТРР, рассчитанные концентрационные зависимости термодинамических характеристик симметричны относительно точки х1 = х2 = 0,5. Экспериментальные зависимости по данным [11] характеризуются явно выраженной асимметрией. Более того, концентрационная зависимость избыточной интегральной энтропии и избыточной парциальной энтропии железа согласно [11] знакопеременна: 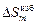 положительна в области, обогащенной железом, и отрицательна при хTi > 0,45. Величина
положительна в области, обогащенной железом, и отрицательна при хTi > 0,45. Величина 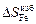 изменяет знак (становится отрицательной) при хTi > 0,8.
изменяет знак (становится отрицательной) при хTi > 0,8.
2. Рассчитанная по заданной величине 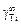 начальная теплота растворения титана в железе в приближении ТКР (-70100 Дж/моль) значительно лучше согласуется с экспериментальной (-78090 Дж/ моль), чем в приближении ТРР (-51339 Дж/моль).
начальная теплота растворения титана в железе в приближении ТКР (-70100 Дж/моль) значительно лучше согласуется с экспериментальной (-78090 Дж/ моль), чем в приближении ТРР (-51339 Дж/моль).
3. В целом точность расчета термодинамических свойств расплавов системы Fе–Тi нельзя признать удовлетворительной. ТКР с параметром t = 7000 К следует рекомендовать только для разбавленных расплавов на основе железа и никеля с целью оценки коэффициента активности по известной теплоте растворения элемента или определения теплоты растворения по заданному коэффициенту активности.
13. Расчет термодинамических свойств бинарных расплавов в приближении квазихимической модели (КХМ)
Задача. Определить коэффициенты активности и теплоты растворения меди и железа в расплавах Fе–Cu, а также интегральные энтальпию, энтропию и энергию Гиббса при 1823 К по известному коэффициенту активности меди в бесконечно разбавленном растворе жидкого железа, используя КХМ.
Исходные данные. Коэффициент активности меди в жидком железе при 1823 К: 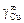 = 10,1; координационное число z = 10 [3].
= 10,1; координационное число z = 10 [3].
Теория. В отличие от ТРР и ТКР, КХМ учитывает упорядочение в расположении атомов. Предполагается, что число связей между атомами 1–1, 2–2 и 1–2 зависит от энергии межатомного взаимодействия. Если раствор образуется с выделением тепла, то преимущественно формируются связи 1–2. В случае, если теплота образования раствора > 0, разнородные атомы стремятся разделиться - число связей 1–1 и 2–2 превышает среднестатистическое. Это приводит к тому, что конфигурационная энтропия отличается от энтропии идеального, регулярного или квазирегулярного растворов, в которых расположение атомов считается хаотическим.
КХМ расплавов основана на квазикристаллической теории жидкости. В КХМ вводят параметр Х таким образом, чтобы произведение NAz Х (NA - число Авогадро, z – координационное число) равнялось числу пар атомов 1 и 2, занимающих соседние узлы квазикристаллической решетки (числу связей 1–2). Этот параметр связан с энергией взаимообмена W соотношением [12]:
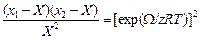 . (1.42)
. (1.42)
Очевидно, что для идеального раствора Х = x1x2; Х > x1x2 , если W < 0 и Х < x1x2 , если W > 0.
Из уравнения (1.42) следует: Х = (2x1x2)/(1 + b), где
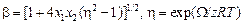 . (1.43)
. (1.43)
Уравнения для расчета теплоты образования сплава и коэффициентов активности его компонентов в приближении КХМ имеют вид:
DН m = Х W = [(2 x1x2)/(1 + b)]W; (1.44)
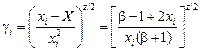 . (1.45)
. (1.45)
Парциальные теплоты растворения компонентов можно рассчитать по уравнению
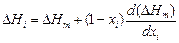 ,
,
где
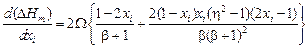 .
.
С помощью уравнений (1.44) и (1.45) можно определить интегральную энергию Гиббса и энтропию:
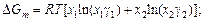
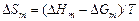 .
.
Таким образом, для расчета термодинамических свойств бинарных расплавов в приближении КХМ необходимо знание двух параметров - энергии взаимообмена W и координационного числа z.
Решение. Для определения неизвестного параметра W воспользуемся заданным значением коэффициента активности меди в жидком железе при 1823 К 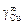 = 10,1. Энергию взаимообмена вычисляем с помощью уравнения (1.45). При х i ® 0, согласно уравнению (1.43), b ® 1. Подстановка хCu = 0 и b = 1 в уравнение (1.45) дает неопределенность (0/0). Чтобы раскрыть ее, воспользуемся правилом Лопиталя: заменим предел отношения функций пределом отношения их производных. В результате получим
= 10,1. Энергию взаимообмена вычисляем с помощью уравнения (1.45). При х i ® 0, согласно уравнению (1.43), b ® 1. Подстановка хCu = 0 и b = 1 в уравнение (1.45) дает неопределенность (0/0). Чтобы раскрыть ее, воспользуемся правилом Лопиталя: заменим предел отношения функций пределом отношения их производных. В результате получим
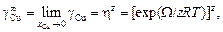
откуда
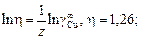
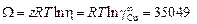 Дж/моль.
Дж/моль.
Рассчитаем термодинамические характеристики расплава Fe–Cu эквиатомного состава (xFe = хCu = 0,5).
Из уравнения (1.43)
b = [1 + 4xFexCu(h2 - 1)]1/2 = [1 + 4×0,5×0,5(1,262 - 1)]1/2 = 1,26.
Тогда
X = 2xFexCu/(1 + b) = 2×0,5×0,5/(1 + 1,26) = 0,221;
DHm = X W = 0,221×35049 = 7754 Дж/моль.
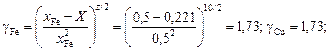
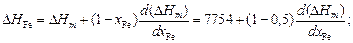
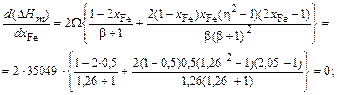
DHFe = DHCu = DHm = 7754 Дж/моль;
DGm = RT [xFeln(xFe gFe) + xCuln(xCu gCu)] =
= 8,34×1823[0,5 ln(0,5×1,73) + 0,5 ln(0,5×1,73)] = -2198 Дж/моль;
DSm = (DHm - DGm)/T = [7754 - (-2198)]/1823 = 5,46 Дж/(моль×К).
Результаты расчета концентрационных зависимостей термодинамических свойств расплавов Fe–Cu приведены в таблице.
Результаты расчета термодинамических свойств расплавов Fе–Cu
при 1823 К в приближении КХМ
| xCu | xFe | b | DHm , Дж/моль | gFe | gCu | aFe | aCu | DGm , Дж/моль | DSm , Дж/(К×моль) | d(DHm )
 dxCu dxCu
| DHCu , Дж/моль | DHFe , Дж/моль |
| 0 | 1,0 | 1,0 | 0 | 1 | 10,1 | 1 | 0 | 0 | 0 | 35087 | 35085 | 0 |
| 0,1 | 0,9 | 1,1 | 3015 | 1,02 | 5,96 | 0,921 | 0,596 | -1918 | 2,71 | 25499 | 25959 | 465 |
| 0,2 | 0,8 | 1,17 | 5162 | 1,10 | 3,98 | 0,880 | 0,797 | -2307 | 4,10 | 17334 | 19030 | 1696 |
| 0,3 | 0,7 | 1,22 | 6624 | 1,23 | 2,88 | 0,861 | 0,864 | -2274 | 4,88 | 11472 | 14663 | 3182 |
| 0,4 | 0,6 | 1,25 | 7478 | 1,43 | 2,14 | 0,858 | 0,857 | -2336 | 5,38 | 5610 | 10844 | 5234 |
| 0,5 | 0,5 | 1,26 | 7768 | 1,72 | 1,72 | 0,859 | 0,859 | -2307 | 5,53 | 0 | 7767 | 7767 |
| 0,6 | 0,4 | 1,25 | 7478 | 2,14 | 1,43 | 0,857 | 0,858 | -2336 | 5,38 | -5610 | 5234 | 10844 |
| 0,7 | 0,3 | 1,22 | 6624 | 2,88 | 1,23 | 0,864 | 0,861 | -2274 | 4,88 | -11472 | 3182 | 14663 |
| 0,8 | 0,2 | 1,17 | 5162 | 3,98 | 1,10 | 0,797 | 0,880 | -2307 | 4,10 | -17334 | 1696 | 19030 |
| 0,9 | 0,1 | 1,1 | 3015 | 5,96 | 1,02 | 0,596 | 0,921 | -1918 | 2,71 | -25499 | 465 | 25959 |
| 1,0 | 0 | 1,0 | 0 | 10,1 | 1 | 0 | 1 | 0 | 0 | -35087 | 0 | 35085 |
Примечания. 1. Рассчитанные по КХМ термодинамические характеристики расплавов Fe–Cu ближе к экспериментальным, чем результаты расчета по ТРР (за исключением энтропии) [3]. Однако использование КХМ, как и ТРР, приводит к ошибочному выводу о расслоении расплава на две несмешивающиеся жидкости.
2. Избыточная энтропия, рассчитанная в приближении КХМ, всегда отрицательна (или равна нулю), так как конфигурационная энтропия не может превосходить энтропию идеального раствора с хаотическим расположением атомов.
3. Название КХМ связано с законом действующих масс для реакции АА + ВВ = 2АВ, поскольку константа реакции
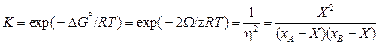 .
.
14. Расчет термодинамических характеристик сплава по диаграмме состояния
Задача. По диаграмме состояния системы Fe–Mn рассчитать теплоты растворения и коэффициенты активности марганца и железа в расплаве Fe–Mn с атомным содержанием марганца 30 % при 1873 К, использовав ТРР.
Исходные данные. 1. Диаграмма состояния Fe–Mn [13] (см. рисунок). 2. Температура и теплота плавления марганца и железа:
Tпл (Мn) = 1517 К, DHпл (Мn) = 14,6 кДж/моль,
Tпл (Fe) = 1809 К, DHпл (Fe) = 15,2 кДж/моль.
Теория. В жидко-твердой области химические потенциалы компонентов в жидкой и твердой фазах при температуре Т, соответствующие равновесию фаз, одинаковы:
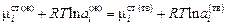 .
.
В качестве стандартного состояния выбираем чистый компонент i в жидком и твердом состояниях соответственно для жидкой 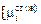
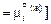 и твердой
и твердой 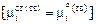 фаз. Учитывая, что
фаз. Учитывая, что
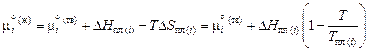
и
а i = giх i ,
получаем следующие уравнения для компонентов бинарного сплава:
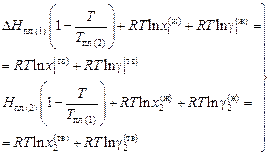 (1.46)
(1.46)
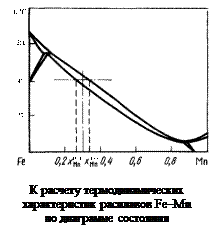 Температура T в двухфазной области и соответствующие ей составы равновесных фаз (точки
Температура T в двухфазной области и соответствующие ей составы равновесных фаз (точки 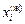 и
и 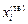 ) определяются из диаграммы состояния (см. рисунок).
) определяются из диаграммы состояния (см. рисунок).
В системе уравнений (1.46) неизвестны четыре коэффициента активности компонентов в жидкой и твердой фазах. Для их определения необходимы еще два уравнения. Воспользуемся приближением ТРР, согласно которому
DH1 = RТ ln g1 = (1 - x1)2W; (1.47)
DH2 = RТ ln g2 = (1 - x2)2W, (1.48)
где W - энергия взаимообмена, является параметром теории.
С учетом выражений (1.47) и (1.48) уравнения (1.46) преобразуется к виду:
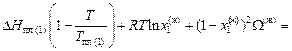
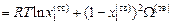 , (1.49)
, (1.49)
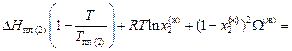
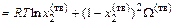 . (1.50)
. (1.50)
Уравнения (1.49) и (1.50) содержат две неизвестные величины и легко разрешаются относительно W(ж) и W(тв).
Решение. Из диаграммы состояния системы Fe–Mn видно, что сплав с атомным содержанием марганца 30 % кристаллизуется в диапозоне температур 1685–1663 К. Рассмотрим равновесие между жидкой и твердой фазами при 1673 К: 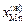 = 0,335;
= 0,335; 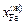 = 0,665;
= 0,665; 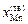 = 0,275;
= 0,275; 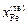 = 0,725. Подставив исходные данные в уравнение (1.49), получим
= 0,725. Подставив исходные данные в уравнение (1.49), получим
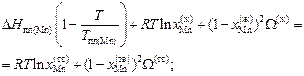
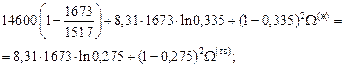
W(тв) = 2354 + 0,840×52(ж).
По уравнению (1.50) вычисляем энергию взаимообмена W(ж):
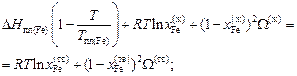
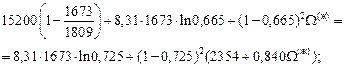
W(ж) = 4742 Дж/моль.
Теплоты растворения и коэффициенты активности марганца и железа в расплаве Fe–Mn (хMn = 0,3) при 1873 К находим по уравнениям (1.47) и (1.48):
DHMn = (1 - xMn)2W = (1 - 0,3)2×4742 = 2324 Дж/моль;
ln gMn = (1 - xMn)2W /RT = 2324/(8,31×1873) = 0,149; gMn = 1,16;
DHFe = (1 - xFe)2 W = (1 - 0,7)2×4742 = 427 Дж/моль;
ln gFe = DHFe /RT = 427/(8,31×1873) = 0,0274; gFe = 1,03.
Примечания. 1. Расчет правильно предсказывает положительные отклонения системы Fe–Mn от закона Рауля.








