Решение. Подставляя в уравнение (1.29) выражения для константы равновесия K и парциального давления а также значения констант F и R, получаем

Дата: 2025-05-01; Просмотры: 2

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

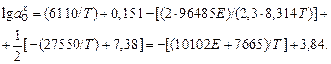
Рассчитанные значения активности кислорода приведены в таблице в исходных данных.

Примечания. 1. В качестве твердого электролита, как правило, применяют стабилизированный диоксид циркония, обладающий практически 100 %-ной ионной (по кислороду) проводимостью. При измерении активности кислорода в хорошо раскисленном металле ([% О] < 0,0010) при высоких температурах (> 1873 К) следует учитывать электронную составляющую проводимости. В этом случае [5]

.

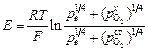Для диоксида циркония, стабилизированного оксидом кальция,

lgp_e = (-68400/T ) + 21,59.

2. Наряду со смесью Мо–МоО₂ (~ 10 % МоО₂) в качестве электрода сравнения часто используют смесь Cr–Cr₂O₃ (2–5 % Cr₂О₃). В этом случае

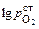= (-39425/T ) + 8,94.

3. На основе определения активности кислорода методом э.д.с. создан прибор для экспрессного определения содержания кислорода в стали [5].

9. Расчет коэффициентов активности компонентов бинарного раствора
с помощью уравнения Гиббса – Дюгема

Задача. С помощью уравнения Гиббса – Дюгема рассчитать коэффициент активности железа в расплавах Fе–Аl при 1873 К по экспериментальным значениям коэффициента активности алюминия.

Исходные данные. Зависимость коэффициента активности алюминия (g_Al) от концентрации в расплавах Fе–Аl при 1873 К [6] приведена в таблице.

Результаты расчета коэффициентов активности железа
в расплавах Fе–А1 при 1873 К с помощью уравнения Гиббса – Дюгема

xAl	xFe		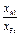-ln gAl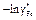
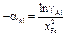
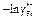
0	1	0	2,38	0	2,38	0
0,1	0,9	0,111	2,20	0,01	2,72	0,005
0,2	0,8	0,250	1,95	0,05	3,05	0,047
0,3	0,7	0,428	1,60	0,18	3,26	0,165
0,4	0,6	0,667	1,25	0,37	3,47	0,374
0,5	0,5	1,00	0,82	0,64	3,30	0,695
0,6	0,4	1,50	0,50	1,02	3,12	1,01
0,7	0,3	2,33	0,24	1,44	2,67	1,58
0,8	0,2	4,00	0,10	1,90	2,50	2,00
0,9	0,1	9,00	0,02	(2,33)	2,0	2,48
1,0	0	¥	0	(2,80)	0	2,84
________________ * Уравнение (1.31). ** Уравнение (1.32).

Теория. Парциальные термодинамические характеристики компонентов бинарного раствора связаны уравнением Гиббса – Дюгема. Для парциальных энергий Гиббса имеем: 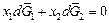. Учитывая, что 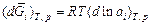и dx₁ = -dx₂ , это уравнение можно записать в виде

(1 – х₂)(¶ lna₁/¶ х₂)_{T, р} = -x₂(¶ lna₂/¶ х₂)_{T, р}.

Отсюда

(1 – х₂)(¶ lng₁/¶ х₂)_{T, р} = -x₂(¶ lng₂/¶ х₂)_{T, р}. (1.30)

Таким образом, если известен коэффициент активности одного из компонентов, например g₂ , то с помощью уравнения (1.30) можно вычислить g₁. Проинтегрировав уравнение (1.30), получим

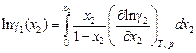
или

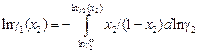. (1.31)

Решение. Определение коэффициента активности железа в расплавах Fe–Аl по заданной концентрационной зависимости коэффициента активности алюминия сводится к вычислению интеграла (1.31). Воспользуемся графическим методом интегрирования. С этой целью строим график зависимости отношения x_Аl/x_Fe от lng_Al (см. рисунок). Заштрихованная на рисунке площадь равна интегралу

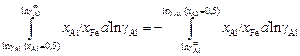
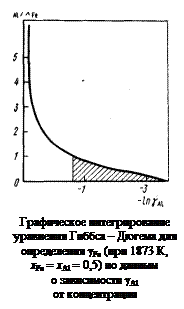и значению lng_Fe при x_Al = x_Fe = 0,5 . Рассчитанная таким образом концентрационная зависимость коэффициента активности железа приведена в таблице вмсте с исходными данными.

Примечания. 1. В области низких концентраций железа графическое интегрирование уравнения (1.31) затруднено по двум причинам. Во-первых, в этой области невысока точность определения величины g_Al , во-вторых, отношение x_Al/x_Fe ® ¥ при x_Fe ® 0, поэтому при низких значениях х_Fe (x_Fe < 0,2; х_Al > 0,8) коэффициенты активности железа получены экстраполяцией зависимости lng_Fe к точке x_Fe = 0.

2. Более удобное для расчета интегральное уравнение Гиббса – Дюгема может быть получено с помощью вспомогательной функции Даркена [7]:

a₂ = lng₂/(1 - х₂)².

Тогда

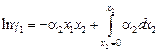. (1.32)

В данном случае подынтегральное выражение ограничено во всем концентрационном интервале 0 £ x₂ £ 1. Функция a_Al и результаты расчета концентрационной зависимости lng_Fe по уравнению (1.32) приведены в таблице.

3. Более точно интегралы в уравнениях (1.31) и (1.32) можно вычислить численными методами (трапеций, Симпсона и др.) с помощью ЭВМ.

4. Для ряда систем коэффициент активности g₂ известен лишь в ограниченной области концентраций от 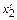до 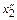. Например, для системы Fе–С при 1873 К величина g_Fe известна в интервале 0,79 £ x_Fe £ 1. В этом случае величину g_C можно рассчитать по уравнению

.

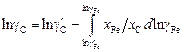Для расчета концентрационной зависимости g_C по этому уравнению необходимо знать величину 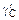при x_Fe = 0,79 ( ).

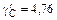10. Расчет стандартной энергии Гиббса
и константы равновесия химической реакции
по справочным данным

Задача. С помощью справочных таблиц определить стандартную энергию Гиббса и константу равновесия реакции восстановления хрома кремнием при 1873 К:

2(Cr₂O₃) + 3[Si] = 4[Cr] + 3(SiO₂). (1.33)

Исходные данные. 1. Значения стандартной энергии Гиббса образования соединений (Дж/моль) заданы в виде: 1) табличных данных при 1873 К [8]: 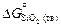= -542070; 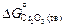= -651079; 2) уравнений [3]: 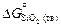= -947000 + 198,0 Т; 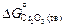= -1131000 + 250,0 Т; 3) приведенной энергии Гиббса при 1873 К [9]: 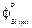= 46,06; 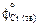= = 51,86; 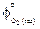= 236,92; 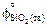= 100,28; 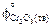= 192,82.

2. Теплота образования диоксида кремния и триоксида дихрома при 0 К [9], Дж/моль: 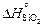= -905717; 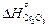= -1134777.

Теория. Стандартной энергией Гиббса химической реакции DG º называют изменение энергии Гиббса системы в результате протекания реакции при условии, что исходные вещества и продукты реакции взяты в стандартных состояниях.

Для кремния, температура плавления которого меньше заданной, за стандартное состояние примем чистый жидкий кремний. Температура плавления остальных компонентов, участвующих в реакции (1.33), превышает 1873 К, поэтому для них в качестве стандартного примем твердое состояние. При таком выборе стандартных состояний стандартная энергия Гиббса DGº равна изменению энергии Гиббса в результате реакции

2Сr₂O_{3 (тв)} + 3Si_(ж) = 4Cr_(тв) + 3SiO_{2 (тв)}. (1.34)

Реакцию (1.34) можно представить как сумму двух процессов:

2Сr₂O_{3 (тв)} = 4Сr_(тв) + 3O_{2 (г)} ; (1.35)

3Si_(ж) + 3O_{2 (г)} = 3SiO_{2 (тв)} . (1.36)

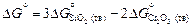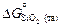Так что , где и 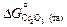- стандартные энергии образования оксидов при 1873 К. Константа равновесия K определяется известным соотношением: DG ^o = -RТ lnК. Для определения энергии образования химических соединений из элементов по уравнениям (1.35) и (1.36) используют справочные таблицы (таблицы стандартных величин), которые составлены по-разному: 1) значения DGº (Т) приведены с определенным шагом по температуре (обычно 100 К); 2) приведены значения коэффициентов А и В, характеризующих температурную зависимость энергии Гиббса: DGº(Т) = А + ВТ, указаны температурные интервалы, в которых коэффициенты А и В принимают постоянными величинами, независимыми от температуры; 3) даны приведенные энергии Гиббса веществ fº(Т):

f°(Т) = -[G°(Т) - 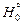]/T, (1.37)

где 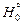- энтальпия вещества при 0 К.

Расчет констант равновесия с использованием приведенных энергий Гиббса (случай 3) проводится по уравнению

RlnK = Df°(Т) – 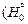/T),

где Df°(Т) - изменение приведенной энергии Гиббса в результате протекания реакции.

Решение. По исходным данным определяем стандартные энергии образования твердого диоксида кремния и кристаллического триоксида дихрома.

1. Из таблиц [8] имеем: 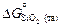= -542070 Дж/моль; 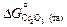= = -651079 Дж/моль.

2. В соответствии с приведенными уравнениями

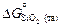= – 947000 + 198,0Т = -947000 + 198,0×1873 =
= -576146 Дж/моль;
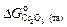= -1131000 + 250,0Т = -1131000 + 250,0×1873 = = -662750 Дж/моль.