Исходные данные. Концентрационная зависимость коэффициента активности gTi в расплавах Ni–Тi при 1800 К [2] (таблица).
Коэффициенты активности титана в расплавах Ni–Ti при 1800 К
| Коэффициент активности титана | Мольная доля титана | ||||||||||
| 0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 | |
| gTi | 0,00238 | 0,0104 | 0,0351 | 0,0935 | 0,202 | 0,364 | 0,560 | 0,748 | 0,896 | 0,976 | 1,0 |
| fTi | 1,0 | 4,29 | 14,2 | 37,1 | 78,6 | 138,9 | 209,4 | 273,8 | 321,2 | 342,0 | 342,9 |
| jTi | 1,0 | 4,37 | 14,8 | 39,3 | 84,9 | 152,9 | 235,3 | 314,3 | 376,5 | 410,1 | 420,2 |
Теория. Величина термодинамической активности может быть определена только относительно того или иного стандартного состояния. Бессмысленно говорить об активности элемента в растворе без указания его стандартного состояния. Это следует из определения активности как
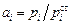 . (1.6)
. (1.6)
Если стандартное состояние, а следовательно, и 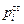 не заданы, то величина ai не может быть определена. Из этого же определения следует, что активность одного и того же элемента при разных стандартных состояниях может иметь значения, отличающиеся на порядок. Ниже будет показано, как можно рассчитать активность элемента в одном стандартном состоянии по данным об активности в другом стандартном состоянии.
не заданы, то величина ai не может быть определена. Из этого же определения следует, что активность одного и того же элемента при разных стандартных состояниях может иметь значения, отличающиеся на порядок. Ниже будет показано, как можно рассчитать активность элемента в одном стандартном состоянии по данным об активности в другом стандартном состоянии.
Рассмотрим раствор, содержащий компонент i (массовая доля в процентах [% i], мольная доля х i). При выборе в качестве стандартного состояния 1 %-ного идеального раствора, подчиняющегося закону Генри, активность компонента i равна
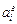 = fi [% i ], (1.7)
= fi [% i ], (1.7)
где fi - коэффициент активности компонента i.
Если за стандартное состояние принять чистый элемент i, то
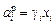 . (1.8)
. (1.8)
В данном случае активность обозначается 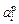 , так как коэффициент активности gi характеризует отклонение от закона Рауля (
, так как коэффициент активности gi характеризует отклонение от закона Рауля ( 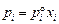 ).
).
Учитывая, что
[% i] = (х i Mi×100)/( х1M1 + х i Mi),
где Mi и M1 - атомные массы растворенного элемента i и растворителя, из уравнений (1.7) и (1.8) получим
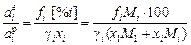 . (1.9)
. (1.9)
Отношение (1.9) не зависит от состава. Для разбавленных растворов ([% i] ® 0, x1 ® 1, fi = 1, gi = 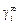 ) оно преобразуется к виду
) оно преобразуется к виду
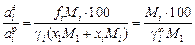 .
.
Отсюда
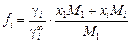 , (1.10)
, (1.10)
что эквивалентно соотношению, полученному К. Люписом [3, с. 24] и [74].
Решение. Рассчитаем коэффициент активности и активность титана в расплаве Ni–Ti эквиатомного состава (хTi = хNi = 0,5):
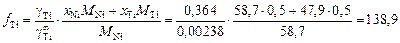 .
.
Мольной доле хTi = 0,5 соответствует [% Тi] = 44,9, при этом 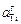 = = fTi [% Тi] = 138,9 × 44,9 = 6237. Большие значения aTi являются результатом значительных положительных отклонений от закона Генри. Рассчитанные величины fTi приведены в таблице,
= = fTi [% Тi] = 138,9 × 44,9 = 6237. Большие значения aTi являются результатом значительных положительных отклонений от закона Генри. Рассчитанные величины fTi приведены в таблице, 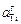 – на рисунке.
– на рисунке.
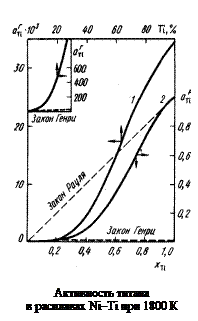 Примечания. 1. Из рисунка следует, что растворы титана в никеле характеризуются отрицательными отклонениями от закона Рауля (gTi < 1) и положительными от закона Генри (fTi > 1). Видно также, что величина
Примечания. 1. Из рисунка следует, что растворы титана в никеле характеризуются отрицательными отклонениями от закона Рауля (gTi < 1) и положительными от закона Генри (fTi > 1). Видно также, что величина 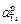 не превышает 1, в то время как
не превышает 1, в то время как 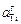 значительно больше 1. Величина
значительно больше 1. Величина 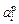 не может быть больше 1, поскольку давление пара компонента над раствором р i всегда меньше, чем над чистым компонентом
не может быть больше 1, поскольку давление пара компонента над раствором р i всегда меньше, чем над чистым компонентом 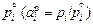 . Величина
. Величина 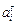 может быть как больше, так и меньше 1, поскольку
может быть как больше, так и меньше 1, поскольку 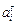 = р i /Г, где Г - постоянная Генри.
= р i /Г, где Г - постоянная Генри.
2. Можно представить гипотетический идеальный раствор, подчиняющийся закону Генри во всей области концентраций. Если концентрацию выразить в мольных долях, то активность компонента i в таком растворе 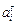 = х i . В данном случае в качестве стандартного состояния рассматривается чистый компонент (х i = 1, тогда
= х i . В данном случае в качестве стандартного состояния рассматривается чистый компонент (х i = 1, тогда 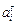 = 1) с такими же свойствами, как в идеальном растворе, подчиняющемся закону Генри. На практике такое стандартное состояние не получило широкого применения. Однако в литературе оно встречается. Коэффициент активности, характеризующий отклонение раствора от закона Генри, в отличие от fi в этом случае обозначают j i =
= 1) с такими же свойствами, как в идеальном растворе, подчиняющемся закону Генри. На практике такое стандартное состояние не получило широкого применения. Однако в литературе оно встречается. Коэффициент активности, характеризующий отклонение раствора от закона Генри, в отличие от fi в этом случае обозначают j i = 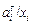 . Из соотношения
. Из соотношения
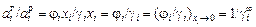
следует, что j i = 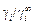 . Рассчитанные значения jTi приведены в таблице.
. Рассчитанные значения jTi приведены в таблице.
3. Для практических расчетов часто используют упрощенное соотношение
f i = 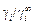 (1.11)
(1.11)
вместо выражения (1.10), т.е. считают, что f i = j i .
Уравнение (1.11) дает хорошие результаты при х i ® 0 или М1 » М i . Для расплава Ni–Тi коэффициент активности f Ti близок к j Ti при хTi < 0,3.
4. Температура плавления титана превышает заданную температуру расплава Т = 1800 К, поэтому в качестве стандартного состояния может быть выбран чистый твердый титан. В этом случае
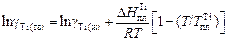 .
.
Учитывая, что 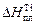 = 18643 Дж/моль,
= 18643 Дж/моль, 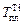 = 1943 К, получим при Т = 1800 К
= 1943 К, получим при Т = 1800 К 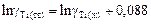 .
.
4. Переход от одного стандартного состояния
к другому
Задача. Определить изменение энергии Гиббса при переходе от стандартного состояния - чистый жидкий алюминий к стандартному состоянию - 1 %-ный раствор алюминия в жидком никеле при 1873 К.
Исходные данные. Коэффициент активности алюминия в разбавленном растворе никеля при 1873 К: 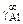 = 0,00025 (стандартное состояние - чистый жидкий алюминий) [3].
= 0,00025 (стандартное состояние - чистый жидкий алюминий) [3].
Теория. Рассмотрим разбавленный раствор компонента А (концентрация [% A], мольная доля xA , fA = 1, gA = 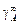 ), полученный в одном случае в результате растворения чистого жидкого компонента Аж :
), полученный в одном случае в результате растворения чистого жидкого компонента Аж :
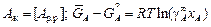 , (1.12)
, (1.12)
в другом случае в результате перехода А из 1 %-ного идеального раствора:
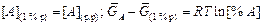 . (1.13)
. (1.13)
Вычитая из уравнения (1.12) выражение (1.13), получаем
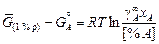 . (1.14)
. (1.14)
Для разбавленного раствора ([% А] ® 0)
[% А] = М A xA ×100/М1, (1.15)
где М1 и М A - атомные массы растворителя 1 и растворенного элемента А. Подставив выражение (1.15) в формулу (1.14), получим
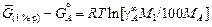 . (1.16)
. (1.16)
Уравнение (1.16) определяет изменение энергии Гиббса (стандартного химического потенциала) компонента А при переходе от стандартного состояния - чистое вещество А к стандартному состоянию - 1 %-ный раствор компонента А.
Решение. Вычислим по уравнению (1.16) изменение энергии Гиббса при 1873 К при переходе от стандартного состояния - чистый жидкий алюминий к стандартному состоянию - 1 %-ный раствор алюминия в жидком никеле:
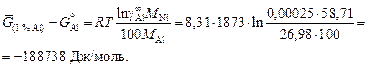
Примечание. Изменение энергии Гиббса при переходе от стандартного состояния - чистый твердый компонент к стандартному состоянию - 1 %-ный идеальный раствор (А(тв) = [А](1 % р) определяется уравнением
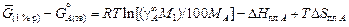 ,
,
где DHпл A и DSпл A - энтальпия и энтропия плавления компонента A.
5. Активность углерода в расплавах Fe–C
Задача. Определить активность углерода в расплавах Fe–C при 1883 К по данным о химическом равновесии
[C] + CO2 (г) = 2CO(г) . (1.19)
Исходные данные. 1. Расплав Fe–C находится в равновесии с газовой смесью CO2 и CO. Отношения 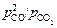 в зависимости от концентрации углерода при 1883 К по данным Ричардсона и Дениса приведены ниже:
в зависимости от концентрации углерода при 1883 К по данным Ричардсона и Дениса приведены ниже:
| [C], % | 0,15 | 0,36 | 0,49 | 0,59 | 0,69 | 0,88 | 1,02 |
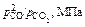
| 10,1 | 20,6 | 29,9 | 41,2 | 51,5 | 66,7 | 80,8 |
2. Константа равновесия реакции
C(гр) + CO2 (г) = 2СО(г) (1.20)
определяется по формуле lgK ¢ = (-8407/T) + 8,76.
Теория. Формула для определения константы равновесия реакции (1.19) имеет вид:
K = 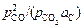 .
.
Если в качестве стандартного состояния для растворенного углерода выбрать графит, то K = K', где K' - константа равновесия реакции (1.20). Тогда
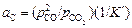 .
.
Решение. Вычислим активность углерода в расплаве, содержащем 0,49 % С. При 1833 К lgK ' = -(8407/1833) + 8,76 = 4,17; K' = 1,48×104.
Константа равновесия K' определена для давления, выраженного в атмосферах. Следовательно, давление должно быть выражено в атмосферах (1 атм = 1,01×105 Па).
Получим K' = 1,48×104×1,01×105 = 1,49×109. Тогда
aС = 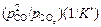 = (29,9×106)/(1,49×109) = 0,026.
= (29,9×106)/(1,49×109) = 0,026.
Рассчитанная таким образом активность углерода в расплавах Fе–С в зависимости от [% С]:
| [С], % | 0,15 | 0,36 | 0,49 | 0,59 | 0,69 | 0,88 | 1,02 |
| aC | 0,0068 | 0,014 | 0,020 | 0,028 | 0,034 | 0,045 | 0,054 |
Примечание. Приведенные исходные данные позволяют определить активность углерода и для стандартного состояния по Генри. Необходимую для этого константу равновесия реакции [С]1 % +
+ CO2 = 2CO можно найти по отношению 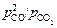 для разбавленного раствора, в котором fС = 1 (см. задачу 6).
для разбавленного раствора, в котором fС = 1 (см. задачу 6).
6. Активность кислорода в жидком железе
Задача. Определить активность и коэффициент активности кислорода в расплавах Fе–О по данным о химическом равновесии расплава с паро-водородной смесью:
Н2 (г) + [О] = Н2O(г). (1.21)
Исходные данные. Расплав железа, содержащий кислород, приводится в равновесие с паро-водородной смесью. Отношения 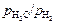 в зависимости от концентрации растворенного в железе кислорода и температуры приведены в таблице (по данным В.В. Аверина).
в зависимости от концентрации растворенного в железе кислорода и температуры приведены в таблице (по данным В.В. Аверина).
Звездочкой отмечены насыщенные растворы кислорода в железе (на поверхности металлического расплава образуется пленочка FеО).
Теория. Константа равновесия реакции (1.21)
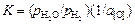 . (1.22)
. (1.22)
Зависимость отношения 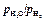 от концентрации и температуры
от концентрации и температуры
| [% O] | pH2O/pH2 | [% O] | pH2O/pH2 | [% O] | pH2O/pH2 | [% O] | pH2O/pH2 |
| T = 1824 K | T = 1847 K | T = 1870 K | T = 1894 K | ||||
| 0,0305 | 0,135 | 0,0344 | 0,132 | 0,0420 | 0,132 | 0,0451 | 0,132 |
| 0,0412 | 0,184 | 0,0385 | 0,132 | 0,0438 | 0,132 | 0,0630 | 0,185 |
| 0,1031 | 0,434 | 0,0464 | 0,184 | 0,0565 | 0,185 | 0,0647 | 0,185 |
| 0,1405 | 0,544 | 0,0898 | 0,322 | 0,1040 | 0,322 | 0,1187 | 0,322 |
| 0,1520 | 0,598 | 0,0887 | 0,322 | 0,1047 | 0,322 | 0,1140 | 0,322 |
| 0,1711 | 0,651 | 0,1570 | 0,540 | 0,1444 | 0,426 | 0,1593 | 0,426 |
| 0,1600 | 0,540 | 0,1763 | 0,540 | 0,2100 | 0,540 | ||
| 0,1697 | 0,598 | 0,1787 | 0,540 | 0,2112 | 0,540 | ||
| 0,2083 | 0,648 | 0,2082 | 0,598 | 0,2502 | 0,648 | ||
| 0,2084 | 0,850 | 0,2248 | 0,735 | ||||
Для расчета активности кислорода должны быть известны отношения 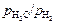 и значения K. Константа равновесия химической реакции зависит только от температуры. Если в качестве стандартного состояния принять разбавленный идеальный 1 %-ный раствор [О], то величину K можно определить по данным в области разбавленных растворов, где f[O] = 1 и a[O] = [% О]. Для этих растворов
и значения K. Константа равновесия химической реакции зависит только от температуры. Если в качестве стандартного состояния принять разбавленный идеальный 1 %-ный раствор [О], то величину K можно определить по данным в области разбавленных растворов, где f[O] = 1 и a[O] = [% О]. Для этих растворов
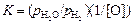 . (1.23)
. (1.23)
Комбинируя уравнения (1.22) и (1.23), определяем активность и коэффициент активности кислорода.
Решение. Для определения константы равновесия реакции (1.21) строим зависимости отношения 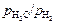 от концентрации растворенного в железе кислорода. Экстраполяцией экспериментальных кривых к точке [ % О] = 0 находим значения K, равные при температурах 1824, 1847, 1870, 1894 К соответственно 4,395; 3,705; 3,220 и 2,805. Активность кислорода в зависимости от состава и температуры вычисляем по уравнению (1.22). Например, при [% О] = 0,1405 и
от концентрации растворенного в железе кислорода. Экстраполяцией экспериментальных кривых к точке [ % О] = 0 находим значения K, равные при температурах 1824, 1847, 1870, 1894 К соответственно 4,395; 3,705; 3,220 и 2,805. Активность кислорода в зависимости от состава и температуры вычисляем по уравнению (1.22). Например, при [% О] = 0,1405 и
Т = 1824 К 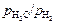 = 0,544 (см. исходные данные), K = 4,395
= 0,544 (см. исходные данные), K = 4,395
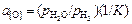 = 0,544/4,395 = 0,124.
= 0,544/4,395 = 0,124.
Отсюда f[O] = a[O]/[% O] = 0,124/0,1405 = 0,881. Результаты расчета f[O] приведены на рисунке.
|
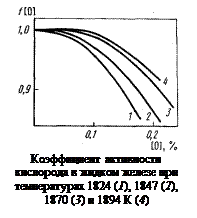 Примечания. 1. Растворы кислорода в жидком железе характеризуются слабыми отрицательными отклонениями от закона Генри (f[O] < 1).
Примечания. 1. Растворы кислорода в жидком железе характеризуются слабыми отрицательными отклонениями от закона Генри (f[O] < 1).
2. Отклонения от закона Генри уменьшаются с повышением температуры; по мере повышения температуры раствор приближается к идеальному разбавленному раствору (f[O] ® 1).
3. Температурная зависимость константы равновесия реакции (1.21), построенная по приведенным данным, имеет следующий вид:
lgK = (9940/T) - 4,536 .
Просуммировав реакцию (1.21) с реакцией образования водяного пара (H2(г) +  O2(г) = H2O(г)), можно определить термодинамические свойства процесса растворения газообразного кислорода в жидком железе (
O2(г) = H2O(г)), можно определить термодинамические свойства процесса растворения газообразного кислорода в жидком железе (  O2(г) = [O]).
O2(г) = [O]).
7. Коэффициенты активности хрома
в расплавах Fе–Сr
Задача. Определить коэффициенты активности хрома в расплавах Fе–Сr при 1873 К по экспериментальным данным о распределении хрома между серебром и железом и заданной активности хрома в жидком серебре.
Исходные данные. 1. Распределение хрома между серебром  и железом
и железом  при 1873 К [4] приведено ниже:
при 1873 К [4] приведено ниже:
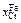 ×100 ×100
| 1,75 | 1,87 | 3,93 | 4,33 | 5,87 | 5,98 | 7,76 | 9,23 |
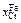 ×100 ×100
| 0,050 | 0,010 | 0,029 | 0,105 | 0,051 | 0,170 | 0,059 | 0,210 |
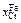 ×100 ×100
| 9,82 | 14,79 | 15,97 | 19,56 | 24,18 | 30,25 | 38,43 | 49,30 |
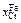 ×100 ×100
| 0,110 | 0,140 | 0,170 | 0,280 | 0,370 | 0,410 | 0,550 | 0,510 |
2. Зависимость коэффициента активности хрома 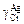 в расплаве Сr–Аg от концентрации хрома
в расплаве Сr–Аg от концентрации хрома 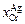 [4] определяется по формуле
[4] определяется по формуле
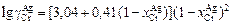 . (1.24)
. (1.24)
Теория. Равновесному распределению элемента i между двумя несмешивающимися жидкостями соответствует равенство химических потенциалов 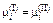 . Учитывая, что
. Учитывая, что 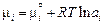 , получаем
, получаем
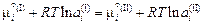 ;
;
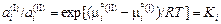 .
.
Если в качестве стандартного состояния выбрать чистое вещество, то 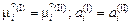 . Учитывая, что ai = gi xi , получаем
. Учитывая, что ai = gi xi , получаем
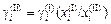 . (1.25)
. (1.25)
Таким образом, для расчета коэффициента активности элемента i в расплаве (II) 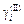 по распределению между несмешивающимися жидкостями (I) и (II) требуются данные о
по распределению между несмешивающимися жидкостями (I) и (II) требуются данные о 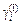 и отношении
и отношении 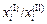 .
.
Решение. Обработка исходных экспериментальных данных методом наименьших квадратов дает следующую зависимость отношения 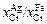 от концентрации хрома в железе:
от концентрации хрома в железе:
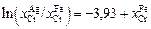 . (1.26)
. (1.26)
Использовав исходные значения 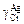 [уравнение (1.24)], а также уравнения (1.25) и (1.26), получим
[уравнение (1.24)], а также уравнения (1.25) и (1.26), получим
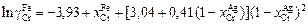 .
.
Рассчитаем коэффициенты активности хрома в разбавленном ( 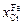 = = 0,01) и концентрированном (
= = 0,01) и концентрированном ( 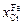 = 0,50) растворах железа. При
= 0,50) растворах железа. При 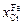 =
=
= 0,01: 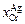 = ехр(-3,93 + 0,01)×0,01 = 2,0×10-4;
= ехр(-3,93 + 0,01)×0,01 = 2,0×10-4; 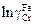 = = -3,93 + 0,01 +
= = -3,93 + 0,01 +
+ [3,04 + 0,41(1 - 2,0×10-4)](1 - 2,0×10-4)2 = -0,47; 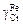 = 0,625.
= 0,625.
При 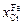 = 0,50:
= 0,50: 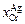 = 0,0324; ln
= 0,0324; ln 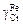 = -0,213;
= -0,213; 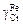 = 0,808.
= 0,808.
Примечания. 1. В соответствии с результатами расчета раствор хрома в железе характеризуется отрицательными отклонениями от закона Рауля.
2. В расчете не учтено влияние незначительного взаимного растворения серебра и железа.
3. Если выбрать в качестве стандартного состояния 1 %-ный раствор компонента i в фазах I и II, то
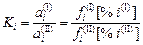 .
.
При сильном разбавлении 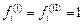 и
и
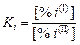 .
.
8. Активность кислорода в жидкой стали
Задача. По значениям э.д.с. кислородного концентрационного элемента определить активность кислорода в жидкой стали 08 кп в конвертере и в ковше.
Исходные данные. 1. Измерена э.д.с. кислородного концентрационного элемента [5]:
| Mo | Mo + MoO2 (электрод сравнения) | ZrO2×Y2O3 (твердый электролит) | Жидкая сталь 08 кп (анализируемый металл) | Mo |
Анализировали пробы металла, отобранные в конвертере и в ковше. Результаты измерения э.д.с. [5] приведены в таблице.
2. Парциальное давление кислорода для электрода сравнения
Mo + MoO2: 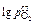 = (-27550/T) + 7,38.
= (-27550/T) + 7,38.
3. Константа равновесия реакции растворения кислорода в жидком железе
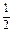 O2(г) = [O], lgK = 6110/T + 0,151.
O2(г) = [O], lgK = 6110/T + 0,151.
Величина э.д.с. кислородного концентрационного элемента и активность кислорода в жидкой стали 08 кп
| Место отбора пробы металла | T, К | Э.д.с., В | aO |
| Конвертер | 1863 | 0,146 | 0,0870 |
| Ковш | 1833 | 0,178 | 0,0482 |
Теория. В приведенном концентрационном элементе э.д.с. возникает вследствие различия термодинамической активности кислорода в анализируемом жидком металле (в стали 08 кп) и электроде сравнения (смеси Мо + МоО2). Величина э.д.с. кислородного концентрационного элемента определяется уравнением Нернста:
Е = (RТ/2F )ln 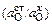 (1.27)
(1.27)
или
Е = (RТ/4F )ln 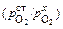 , (1.28)
, (1.28)
где F - электрохимическая постоянная (число Фарадея), F = 96485 Кл/моль; 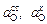 – активность кислорода в электроде сравнения и в анализируемом металле;
– активность кислорода в электроде сравнения и в анализируемом металле; 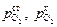 - парциальное давление кислорода в газовой фазе, равновесной с электродом сравнения и исследуемым расплавом соответственно.
- парциальное давление кислорода в газовой фазе, равновесной с электродом сравнения и исследуемым расплавом соответственно.
В качестве электрода сравнения выбирают вещество с известной активностью или равновесным парциальным давлением кислорода. В соответствии с уравнением (1.28)
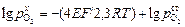 .
.
Для определения величины 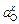 воспользуемся константой равновесия реакции растворения кислорода:
воспользуемся константой равновесия реакции растворения кислорода:
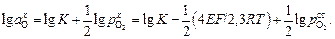 (1.29)
(1.29)








